„Hideg-meleg” változatai közötti eltérés

A lap 2011. február 9., 08:44-kori változata (lapforrás) FiziSysop (vitalap | szerkesztései) (Új oldal, tartalma: „<wlatex> Newton törvényeivel leírhatjuk makroszkopikus tárgyak mozgását a bolygóktól a biliárdgolyókig. Viszont egy kisebb szobában található mintegy <math>10…”)		A lap jelenlegi, 2011. május 12., 15:55-kori változata (lapforrás) Vanko (vitalap | szerkesztései)
(2 szerkesztő 2 közbeeső változata nincs mutatva)
1. sor:		1. sor:
		+	[[Kategória:Szerkesztő:Vankó]]
	<wlatex>		<wlatex>
−	Newton törvényeivel leírhatjuk makroszkopikus tárgyak mozgását a bolygóktól a biliárdgolyókig. Viszont egy kisebb szobában található mintegy <math>10^{27}</math> gázmolekula mozgását reménytelen, és értelmetlen egyenként követni. Szerencsére a statisztikus fizika segítségével a nagyszámú részecske átlagos jellemzői (pl. hőmérséklet, nyomás) közötti összefüggéseket pontosan megérthetjük. A statisztikus fizika számos komplex rendszer leírására is alkalmas, a természetben előforduló érdekes mintaképződésektől az internet vagy pénzügyi folyamatok modellezésén keresztül a kollektív mozgások (pl. közlekedési dugók) megértéséig. Ezen komplex folyamatok megértésében a statisztikus fizikán alapuló számítógépes szimulációknak kiemelkedő jelentősége van.	+	A komfort érzetünk egyik fontos tényezője hogy télen a meleg szobát, nyáron a hűvös, árnyas helyeket keressük. A „hideg és a meleg” iránti vágyunk kielégítése pénzbe kerül. Télen fűtűnk, nyáron hűtünk. De a technika világában a „melegedés” igen káros is lehet. Egy számítógép belsejében a hő mindig termelődik, így a processzor hűtése létfontosságú a berendezés megbízható működéséhez.
		+
		+	A hőátadási folyamatok fizikai alapjait jól ismerjük. Fel- és kihasználásuk a mérnöki munka egyik igen fontos területe. Hol termelni, hol „megszüntetni” akarjuk. A célt mindig az elérni kívánt eredmény határozza meg.
	__TOC__		__TOC__
−	==Mikroszkopikus és makroszkopikus leírás==	+	==Hőfelszabadulás==
−	===A hőmérséklet kinetikus értelmezése===	+	===Hőfelszabadulás számítógépekben és élő szervezetekben===
−	Egy egyensúlyban lévő rendszer állapotát jellemezhetjük a makroszkopikus állapotjelzőkkel. Az állapotjelzők csak a rendszer pillanatnyi állapotától függenek, függetlenek a rendszer előéletétől. Az [http://en.wikipedia.org/wiki/Intensive_and_extensive_properties#Extensive_properties extenzív állapotjelzők] a rendszer méretével együtt nőnek, két rendszer egyesítésekor összeadódnak: ilyen pl. a térfogat, a tömeg, a mólszám, a [[#Belső energia|belső energia]] és az [[#Az entrópia termodinamikai értelmezése, a II. főtétel megfogalmazása entrópiával|entrópia]]. Az [http://en.wikipedia.org/wiki/Intensive_and_extensive_properties#Intensive_properties intenzív állapotjelzők] – pl. a [http://en.wikipedia.org/wiki/Temperature hőmérséklet], a [http://en.wikipedia.org/wiki/Pressure nyomás], a [http://en.wikipedia.org/wiki/Chemical_potential kémiai potenciál] és a sűrűség – a rendszer méretétől függetlenek, két rendszer egyesítésekor átlagolódnak.	+	A számítógépekben (és más berendezésekben), valamint élő szervezetekben is folyamatosan hő szabadul fel, azaz külső vagy belső energiaforrások növelik a gép vagy az élő szervezet egyes részeinek belső energiáját. A hőfelszabadulásnak nagyon sokféle oka lehet.
−	A hőmérséklet értelmezéséhez több lépésben juthatunk el. A fogalom a hétköznapi tapasztalatból származik: érzékszerveinkkel meg tudunk különböztetni hideg és meleg testeket. Az érzékelés azonban meglehetősen szubjektív: például ugyanazt a langyos vizet melegnek vagy hidegnek fogjuk érezni attól függően, hogy előtte a kezünk hideg vagy forró vízben volt-e. A hőmérséklet objektív mérését az teszi lehetővé, hogy az anyagok számtalan tulajdonsága hőmérsékletfüggő. A hagyományos higanyos vagy alkoholos hőmérőkben a folyadékok hőtágulása, az elektromos hőmérőkben pedig legtöbbször az anyagok hőmérsékletfüggő fajlagos ellenállása alapján mérjük a hőmérsékletet.	+	Az élő szervezetekben az izmok munkavégzéséhez szükséges energiát a táplálékkal felvett szerves anyagok kémiai oxidációja fedezi. Ilyen szempontból az élő szervezet lényegében egy hőerőgép, amelyre természetesen igaz a [[Rend és rendetlenség#A hőtan II. főtétele |II. főtétel]]: termikus hatásfoka egynél kisebb. Ezért a munkavégzéssel együtt szükségszerűen hőfelszabadulás jár. (Ugyanez az oka a belsőégésű motorral üzemelő járművekben felszabaduló hő döntő többségének is.) Ez a felszabaduló hő pótolja a szervezet hőleadását, és így képes a melegvérű állatokat (és az embert) állandó, a környezeténél általában magasabb hőmérsékleten tartani. Az állandó hőmérséklet megtartásához azonban a hőtermelést és a hőleadást egyensúlyban kell tartani.
−	A hétköznapi életben a hőmérséklet méréséhez a [http://en.wikipedia.org/wiki/Celsius Celsius-skálát] használjuk, melynek két rögzített pontja a víz fagyáspontja (0 °C) és a víz forráspontja normál légköri nyomáson (100 °C). A fizikában a hőmérséklet mértékegysége a kelvin (K): a termodinamikai (vagy abszolút) hőmérsékleti skála egysége megegyezik a Celsius-skála egységével, de nullpontja az un. abszolút nulla fok (-273,15 °C = 0 K).	+	A számítógépekben nincs hőerőgép, de például a mozgó alkatrészek súrlódása, az áramjárta vezetékekben felszabaduló [http://en.wikipedia.org/wiki/Joule%27s_laws Joule-hő], a mágneses anyagok (adathordozók, transzformátorok) [http://en.wikipedia.org/wiki/Hysteresis hiszterézise] folyamatosan hőt „termel”. A hőfelszabadulás aránylag kis méretű alkatrészekben (pl. a processzorban vagy a merevlemez író-olvasó fejében) különösen koncentráltan történik, és így ezek hűtésére különösen figyelni kell.
−	Az állapotjelzők nem függetlenek egymástól, különböző rendszereknél más-más kapcsolat írható fel közöttük. A valóságos rendszereket különböző modellekkel lehet leírni. Egyszerűsége, elméleti és gyakorlati jelentőssége miatt is kiemelkedő fontosságú modell az [http://en.wikipedia.org/wiki/Ideal_gas ideális gáz]. Az ideális gáz modellben a molekulák között – az ütközéseket kivéve – nincs kölcsönhatás, és a molekulák össztérfogata sokkal kisebb, mint a tartály térfogata. A hétköznapi életben a nem túl nagy sűrűségű gázok jó közelítéssel ideális gáznak tekinthetők.	+	===A hőátadás módjai===
		+	A termodinamika II. főtétele szerint a hőátadás mindig a melegebb testről a hidegebb irányába történik. A folyamat azonban több, lényegesen különböző módon történhet:
−	Az ideális gáz makroszkopikus állapotjelzői között a tapasztalat szerint a $$pV=nRT$$	+	A [[#A hővezetés |hővezetés]] elsősorban szilárd testeken belül meghatározó folyamat. (Folyadékokban és gázokban csak akkor figyelhető meg önmagában, ha nem jöhet létre áramlás.) A rezgő atomok és molekulák közötti kölcsönhatás eredményeképpen a gyorsabban rezgő részecskék átlagosan több mozgási energiát adnak át a lassabb részecskéknek, mint viszont. Az energiatranszport tehát a hővezetésnél nem jár részecsketranszporttal.
−	kapcsolat írható fel, ahol $p$ a gáz nyomása, $V$ a térfogata, $n$ a mólszám, $T$ az abszolút hőmérséklet és $R$ = 8,314 J/molK az egyetemes gázállandó. A gáz nyomása (a tartály falának egységnyi területű darabjára ható erő) a tartály falának ütköző, és onnan visszaverődő molekulák impulzusváltozásából ered. A gáz homogén és izotróp, így a molekulák egyforma valószínűséggel haladnak minden irányba. A gázmolekulák nem egyforma sebességgel mozognak (sebességeloszlásukat a [http://en.wikipedia.org/wiki/Maxwell_distribution#Distribution_for_the_speed Maxwell-eloszlás] adja meg), de számításunkban csak a sebességek négyzetes középértékére ($\widehat{v}$) van szükség.	+	A [[#A hőáramlás|hőáramlás]] folyadékokban és gázokban lehetséges. Ekkor a hőátadás úgy történik, hogy az átlagosan nagyobb energiájú részecskék áramlással a melegebb helyről a hidegebb helyre kerülnek (míg az átlagosan kisebb energiájúak éppen fordítva, a hidegebb helyről a melegebb helyre áramlanak). Itt tehát az energiatranszport a részecsketranszporttal együtt történik.
−	[[Fájl:5001_kinetikus_gazelmelet.jpg|bélyegkép|200px|1. ábra]]	+	Az előzőektől teljesen eltérő folyamat a [[#A hősugárzás |hősugárzás]], amikor a testek közti hőátadás elektromágneses sugárzás segítségével jön létre. Az elektromágneses hullámok vákuumban is terjednek, a világűrben csak így lehetséges hőátadás. Ugyanakkor a hősugárzásnak a földi folyamatokban is nagyon fontos szerepe van.
−	Az egyszerűség kedvéért úgy számolunk, mintha minden molekula a $\widehat{v}$ négyzetes középsebességgel mozogna. A Pitagorasz-tétel alapján $$\widehat{v}^2=\widehat{v}_x^2+\widehat{v}_y^2+\widehat{v}_z^2=3\widehat{v}_x^2$$ hiszen az izotrópia miatt a három sebességkomponens egyenlő. Egyetlen, az x-irányra merőleges falnak ütköző és onnan visszapattanó molekula impulzusváltozása $\Delta I_{\mu}=-2\mu\widehat{v}_x$, ahol $\mu$ a molekula tömege. A falat $\Delta t$ idő alatt azok a részecskék érik el, amelyek legfeljebb $\widehat{v}_x\Delta t$ távolságra vannak a faltól, és a fal felé mozognak. Ezek száma $$\Delta N=\frac{N}{2}\frac{\widehat{v}_x\Delta t A}{V}$$ ahol $N$ az összes részecske száma (a szimmetria miatt ezek fele mozog a fal felé). A falra ható erő $$F=-\frac{\Delta I}{\Delta t}=\frac{N}{2}\frac{\widehat{v}_x\Delta t A}{V}\frac{2\mu\widehat{v}_x}{\Delta t}=\frac{\mu\widehat{v}_x^2 N A}{V}=\frac{\mu\widehat{v}^2 N A}{3V}$$ Ennek alapján a nyomás $$p=\frac{F}{A}=\frac{2}{3}\frac{1}{2}\mu\widehat{v}^2\frac{N}{V}=\frac{2}{3}\bar{\varepsilon}_h\frac{N}{V}$$ ahol $$\bar{\varepsilon}_h=\frac{1}{2}\mu\widehat{v}^2$$	+
−	a molekulák átlagos haladó mozgási energiája.	+	==A hővezetés==
		+	===A hővezetés törvényei===
		+	A hőáram az időegység alatt szállított hő: $$J_Q=\frac{\Delta Q}{\Delta t}$$ A tapasztalat szerint egy homogén, állandó keresztmetszetű rúdban (vagy egy homogén falon keresztül) a hőáram egyenesen arányos a rúd két vége (illetve a fal két oldala) közti $\Delta T$ hőmérséklet-különbséggel valamint a rúd $A$ keresztmetszetével (a fal felületével), és fordítva arányos a rúd $l$ hosszával (a fal vastagságával): $$J_Q=\lambda \frac{A}{l}\Delta T$$
−	Az eredményt összevethetjük az ideális gáz állapotegyenletével: $$pV=\frac{2}{3}\bar{\varepsilon}_h N=nRT$$ $$\bar{\varepsilon}_h=\frac{3}{2}\frac{n}{N}RT=\frac{3}{2}\frac{R}{L}T=\frac{3}{2}kT$$ ahol $$L=6,02\cdot 10^{23}\,{\rm 1/mol}$$ az [http://en.wikipedia.org/wiki/Avogadro_constant Avogadro-szám] és $$k=\frac{R}{L}=1,38\cdot 10^{-23}\,{\rm J/K}$$	+	A $\lambda$ hővezetési tényező az anyagra jellemző állandó.
−	a [http://en.wikipedia.org/wiki/Boltzmann_constant Boltzmann-állandó].	+	Általános esetben a hővezetés a $\vec{j}_Q$ hőáramsűrűség-vektorral (az egységnyi felületen áthaladó hőáram) jellemezhető. A hőáramsűrűség egyenesen arányos a hőmérséklet-gradienssel ([http://en.wikipedia.org/wiki/Heat_conduction#Fourier.27s_law Fourier-törvény]): $$\vec{j}_Q=-\lambda\nabla T$$
−	A molekulák sebességének négyzetes középértéke $$\widehat{v}=\sqrt{\frac{3kT}{\mu}}=\sqrt{\frac{3RT}{M}}$$	+	Észrevehető, hogy az összefüggés analóg az elektromos vezetés [http://en.wikipedia.org/wiki/Ohm%27s_law Ohm-törvényével]. Az $A$ keresztmetszetű, $l$ hosszúságú vezetőn folyó $I$ áramerősség (időegység alatt szállított töltés): $$I=\sigma\frac{A}{l}U$$ ahol , $U$ a feszültség (potenciálkülönbség), és $\sigma$ a fajlagos vezetőképesség (a fajlagos ellenállás reciproka).
−	ahol $M$ a moláris tömeg. Szobahőmérsékletű nitrogén esetében az átlagos sebesség kb. 500 m/s.	+	Differenciálisan pedig $$\vec{j}=-\sigma\nabla\Phi=\sigma\vec{E}$$
−	Ezek az összefüggések kapcsolatot teremtenek a mikroszkopikus állapotjelzők (molekulák átlagos sebessége, átlagos mozgási energiája) és a makroszkopikus állapotjelzők (nyomás, hőmérséklet) között.	+	ahol $\vec{j}$ az áramsűrűség-vektor, $\Phi$ az elektromos potenciál és $\vec{E}=-\nabla\Phi$ az elektromos térerősség.
−	==A hőtan I. főtétele==	+	Az analógia lehetővé teszi összetett hővezetési problémák elektromos modellezését: ellenállásokat bekötni, feszültségeket és áramerősségeket mérni sokkal egyszerűbb, mint hővezető szerkezeteket megépíteni, hőmérsékleteket és hőáramokat mérni.
−	===Belső energia===	+
−	Egy rendszer [http://en.wikipedia.org/wiki/Internal_energy belső energiája] a benne lévő részecskék tömegközépponthoz viszonyított mozgási energiájának és a részecskék közti erőkből származó potenciális energiának az összege. Mozgási energia a szabadon mozgó részecskék haladó mozgásából, a molekulák forgásából és belső rezgéséből, illetve szilárd anyagoknál az atomok és molekulák rácshely körüli rezgéséből származik.	+
−	Az ideális gázban a molekulák közt (az ütközéseket kivéve) nincs kölcsönhatás, így a potenciális energia nulla. A mozgási energia az egyes atomok mozgási energiájának összege. Egyatomos molekulák (nemesgázok) esetében a molekuláknak csak haladó mozgási energiája van. (Az atomok tömegének 99,8 %-a az atomnál 5 nagyságrenddel kisebb átmérőjű atommagban van, így az pontszerűnek tekinthető.) Kétatomos (és többatomos lineáris molekulák) a molekula tengelyére merőleges két tengely körül, többatomos térbeli molekulák pedig három tengely körül foroghatnak, amelyhez szintén mozgási energia („forgási energia”) tartozik.	+	A legjobb hővezetők egyben jó elektromos vezetők is (ezüst, vörösréz, alumínium), aminek az az oka, hogy a szabad elektronoknak nemcsak az elektromos vezetésben, hanem a hővezetésben is fontos szerepük van.
−	Az [http://en.wikipedia.org/wiki/Equipartition_theorem ekvipartíció tétele] szerint minden [http://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry) szabadsági fokra] átlagosan ugyanakkora energia jut. Az egyatomos gázban a molekuláknak 3 szabadsági foka van (3 dimenzióban mozoghat), a kétatomos gázban 5 (3 a haladó mozgásból + 2 a két tengely körüli forgásból), a többatomos gázokban pedig 6 (3 haladó + 3 forgó mozgásból). Nagyobb molekuláknál, vagy magasabb hőmérsékleten a molekulák rezgéseihez is tartozhat szabadsági fok. Az ekvipartíció tétele nem csak gázokra, hanem más rendszerekre is igaz: a szilárd testek rezgő atomjainak például 6 szabadsági foka van (3 mozgási energia + 3 potenciális energia tagból).	+	===Különleges hőszigetelő anyagok===
		+	Legjobb hőszigetelő a vákuum: azon keresztül csak hősugárzással lehet hőcsere. Így „működik” az acél termosz: a két, egymáshoz közeli, vékony fal közti levegőt kiszívják. (A falak közti hősugárzást pedig fényes, tükröző felületekkel [[#Abszorpció és emisszió: miért fekete a hűtőborda?|csökkentik]].)
−	Az egyatomos gázban a molekulák átlagos mozgási energiája $$\bar{\varepsilon}_m=\bar{\varepsilon}_h=\frac{3}{2}kT$$ Ez az energia 3 szabadsági fok között oszlik meg, így az egy szabadsági fokra jutó átlagos energia $$\bar{\varepsilon}_0=\frac{1}{2}kT$$ Ha a molekulának $f$ szabadsági foka van, akkor a molekula átlagos mozgási energiája $$\bar{\varepsilon}_m=\frac{f}{2}kT$$	+	A gázok is elég jó szigetelők lennének, ha nem alakulnának ki áramlások. A lyukacsos, porózus szerkezetekben az egymástól elzárt (és így az áramlásban akadályozott) levegőrétegek szigetelnek.
−	Az ideális gáz belső energiája így $$E=N\bar{\varepsilon}_m=\frac{f}{2}NkT=\frac{f}{2}nRT$$	+	Az űrsiklók burkolására olyan speciális [http://en.wikipedia.org/wiki/Space_Shuttle_thermal_protection_system#Detailed_description kerámiát] fejlesztettek ki, amely kellő szilárdságú, és ugyanakkor nagyon jó hőszigetelő. (A légkörbe való belépéskor a nagyon nagy sebesség miatt az űrsikló felülete felforrósodik.) Ez az anyag olyan rossz hővezető, hogy ha vörösen izzik, akkor is kézbe lehet venni: A bőrünk lehűti a kerámia felületét, és az nem melegszik fel újra a rossz hővezetés miatt. (Ugyanezért nem éget a szauna 100 °C-os fa burkolata sem, pedig az ugyanilyen meleg víz, vagy fém tárgyak már égési sérülést okoznak.)
−	A belső energia az ideális gáznál tehát csak a hőmérséklettől függ. Más anyagoknál a belső energia a többi állapotjelzőtől is függhet (lásd pl. [http://en.wikipedia.org/wiki/Van_der_Waals_equation Van der Waals-gáz]).	+	==A hőáramlás==
		+	===Gravitációs áramlások===
		+	A folyadékok és gázok sűrűsége függ a hőmérséklettől: általában a hőmérséklet növelésével csökken. (Kivétel pl. a víz 0 °C és 4 °C között.) Emiatt ha egy folyadék vagy gáz alját melegítjük (vagy tetejét hűtjük), akkor a közegben a gravitáció hatására [http://en.wikipedia.org/wiki/Convection áramlások] alakulnak ki: a meleg (kisebb sűrűségű) anyag felfelé, a hideg (nagyobb sűrűségű) lefelé mozdul el. A hőáramlás csökkenti a közeg alja és teteje közti hőmérséklet-különbséget, de ha a közeg alját folyamatosan melegítjük (vagy a tetejét hűtjük), akkor folyamatos áramlás alakulhat ki. A gravitációs áramlásra rengeteg példát láthatunk a természetben és a hétköznapi gyakorlatban is.
−	===Munkavégzés és hőközlés===	+	A napsugárzás elsősorban a talajban és a vízfelületeken nyelődik el, azt melegíti fel. A talajtól és a víztől felmelegedő (nedves) levegő felszáll, és eközben kitágul, adiabatikusan lehűl (és a benne lévő vízgőz kicsapódik) – ez a globális légmozgások alapvető hajtóereje.
−	A rendszer belső energiája csak akkor változhat meg, ha a rendszer a környezettől energiát kap vagy a környezetnek energiát ad le. Az energiaátadásnak két lényegesen különböző módja van: a [http://en.wikipedia.org/wiki/Work_(thermodynamics) munkavégzés] és a [http://en.wikipedia.org/wiki/Heat hőközlés].	+
−	Ha a rendszer kitágul, akkor a környezetén munkát végez. A rendszer összenyomásához viszont külső munkavégzés szükséges (ilyenkor a rendszer munkavégzése negatív). Az elemi munkavégzés $${\rm d}W=p{\rm d}V$$ a rendszer által végzet munka (miközben egy meghatározott folyamat során az 1-es állapotból a 2-es állapotba kerül): $$W=\int_1^2 p{\rm d}V$$	+	A fűtőtesttől felmelegedő levegő felszáll, a szobában áramlás alakul ki. Ez szállítja a fűtőtest melegét a szoba többi részébe. Eközben a levegő lehűl, és a szoba másik oldalán leszáll – így záródik az áramlás. Ehhez hasonlóan a kémények huzatát szintén a gravitációs áramlás biztosítja: a kinti levegőnél melegebb füst felfelé száll.
−	A munkavégzés az energiaátadás „rendezett” módja: pl. a tartályt elzáró dugattyú valamilyen irányban elmozdul. (A munkavégzés az elmozdulás irányától függően pozitív vagy negatív lehet.) Bár mechanikai elmozdulás nem történik, termodinamikai szempontból munkavégzés a termoelemben keletkező elektromos munka, illetve a [[#Peltier-elem: a számítógépben használt hűtőgép|Peltier-elemben]] a rendszerrel közölt elektromos munka is.	+	Központi fűtés is építhető gravitációs áramlással: a kazánban felmelegedő víz az egyik csövön a pincéből felfelé, a fűtőtestekben kihűlő víz a másik csövön lefelé áramlik. A tűzhelyre tett lábasban is a folyadékban kialakuló gravitációs áramlás szállítja a hőt a lábas aljáról a felsőbb rétegekbe. (Viszkózusabb folyadékokban nem alakul ki elég erős áramlás, így az étel a lábas alján túlzottan felforrósodik, és az étel odaég. Ilyenkor az ételt [[#Kényszerített áramlások |keverni]] kell.)
−	A hőközlés az energiaátadás „rendezetlen” módja: úgy jön létre energiaátadás, hogy a két rendszer (vagy a rendszer és környezete) hőmozgásban lévő részecskéi véletlenszerű ütközésekkel adnak át energiát egymásnak. A [[#A II. főtétel néhány megfogalmazása|tapasztalat]] szerint azonban a magasabb hőmérsékletű rendszer (átlagosan nagyobb energiájú) részecskéi az ütközések során átlagosan több energiát adnak át az alacsonyabb hőmérsékletű (átlagosan kisebb energiájú) részecskéinek, mint viszont. Emiatt ez az energiaátadási forma meghatározott irányú: mindig a melegebb test ad át energiát a hidegebb testnek. A hőközléskor a rendszer által felvett energiát (a „hőt”) $Q$-val jelöljük.	+	Télen a tavak és tengerek felülete kezd el hűlni, a hideg víz lesüllyed, ezzel gyorsítva az egész víztömeg kihűlését. A folyamat azonban csak 4 °C-ig tart: az ennél hidegebb víz már kisebb sűrűségű, mint a 4 °C-os, így az a felszínen marad. Emiatt először a felszínen fagy meg a víz. A jégréteg viszont már rosszabb hővezető, lassítja az alatta lévő víz hűlését és megfagyását, így az aránylag sekély vizek se fagynak be fenékig. Ennek rendkívüli jelentőssége volt a sekély vizekben kialakuló földi élet szempontjából (és ma is ez teszi lehetővé a vízi élőlények áttelelését).
−	A [http://en.wikipedia.org/wiki/First_law_of_thermodynamics termodinamika I. főtétele] azt fogalmazza meg, hogy a rendszer belső energiája nem változhat meg magától (energia nem keletkezik, vagy tűnik el), hanem csak akkor, ha a rendszer a környezettől energiát kap vagy a környezetnek energiát ad le: $$\Delta E=Q-W$$	+	Ha egy vékony, viszkózus folyadékréteget egyenletesen melegítünk alulról, akkor a szimmetria miatt sokáig nem alakul ki áramlás (a folyadék „nem tudja eldönteni”, hogy hol kezdjen el felfelé, és hol lefelé áramlani). Amikor a sűrűségkülönbség már nagy lesz, akkor az instabil egyensúly valahol felborul: a meleg anyag bizonyos helyeken felfelé, körülötte a hideg pedig lefelé fog áramlani. Ilyen [http://en.wikipedia.org/wiki/Rayleigh-B%C3%A9nard_convection áramlási mintázatokat] meg lehet figyelni egy vékony, alulról melegített olajrétegben is, de a Nap felületén is (ahol az égitest belsejében zajló fúzió által felforrósodott anyag áramlik a hidegebb felszín felé).
−	Az I. főtétel azt is kifejezi, hogy az energiaátadásnak két lényegesen különböző módja van. (A munkavégzés előtt azért van negatív előjel, mert $W$ a rendszer által végzett munka.)	+	===Kényszerített áramlások===
		+	Súlytalanság állapotában (például műholdakon), vagy ha a közeg fent melegebb, mint lent, gravitációs áramlás egyáltalán nem alakul ki. Más esetekben – például ha az áramlás kialakulásához rendelkezésre álló tér szűk, vagy a csövek vékonyak – a kialakuló áramlás nem elég intenzív a kellő intenzitású hőátadáshoz. Ilyenkor kényszerített áramlásra van szükség, az áramlást ventillátorral, keringtetőszivattyúval lehet kialakítani vagy fokozni.
−	==A hőtan II. főtétele==	+	A számítógépekben (gyakran kellemetlenül zajos) ventillátorok biztosítják a kellő hőcserét. A mai központi fűtések pedig keringtető szivattyúval készülnek (így vékonyabb csövek kellenek – viszont a gázfűtés áramszünetkor is leáll). Legtöbb autóban mind a kettőt alkalmazzák: a motorban felszabaduló hőt a vízpumpával hajtott hűtővíz szállítja a hűtőbe, ahonnan – szükség esetén ventillátorral hajtott – levegő szállítja tovább.
−	===Hőerőgép, hőszivattyú, hűtőgép===	+
−	Az I. főtétel szerint egy rendszer belső energiája hőközléssel és munkavégzéssel is megváltoztatható. Ez lehetővé teszi olyan berendezések készítését, melyek hőközlés hatására mechanikai munkát végeznek ([http://en.wikipedia.org/wiki/Heat_engine hőerőgép]), illetve mechanikai munka segítségével hidegebb helyről a melegebb felé hoznak létre hőtranszportot ([http://en.wikipedia.org/wiki/Heat_pump hőszivattyú], [http://en.wikipedia.org/wiki/Refrigerator hűtőgép]).	+
−	A járművekben használt benzin- és dízelmotorok, a gőzgépek, az atom- és hőerőművekben használt gőz- és gázturbinák, a repülőgépek sugárhajtóműve mind hőerőgépek: különböző anyagok elégetése vagy az urán hasadása közben felszabaduló hőt alakítják (részben) mechanikai munkává – amely a járművekben közvetlenül hasznosul, az erőművekben pedig az elektromos energiát előállító generátorokat működteti. A különböző hőerőgépekben különböző termodinamikai folyamatok játszódnak le, és más-más technikai megoldásokat alkalmaznak, de a hőerőgépek lényegét egyszerűbb modelleken is megérthetjük.	+	===A hőátadás fokozása halmazállapot-változással===
		+	A testek felületén a hő átadódik a szilárd test és a környező gáz vagy folyadék között. A hőátadás mértéke értelemszerűen függ a felület nagyságától, de ezen kívül sok más paramétertől is. A közeg áramlása például jelentősen növeli a hőátadás intenzitását. Így nem mindegy a felület iránya sem, hiszen függőleges felület mellett könnyebben alakul ki gravitációs áramlás.
−	Ha vizet forralunk (hőt közlünk vele), akkor a felszabaduló vízgőz térfogata megnő, és eközben munkát végez. Ez egy nagyon egyszerű hőerőgép. Azonban ahhoz, hogy a berendezés folyamatosan működjön, a vizet is folyamatosan pótolni kell, vagy a keletkező és kitáguló vízgőzt kell visszaalakítani vízzé. Ilyen módon ciklikusan működő berendezést hozhatunk létre. A víz-vízgőz rendszer viselkedésének leírása a halmazállapot-változás miatt bonyolultabb, azonban hőerőgép ideális gázon végzett körfolyamatok segítségével is létrehozható. Ezek közül elméleti szempontból a [http://en.wikipedia.org/wiki/Carnot_cycle Carnot-ciklus] a legfontosabb. A 2. ábrán [http://en.wikipedia.org/wiki/P-V_diagram p-V állapotsíkon] ábrázolt körfolyamat négy részből áll:	+	A hőátadás intenzitását nagymértékben fokozza a felületen végbemenő halmazállapot-változás: a párolgó folyadék jelentős hőmennyiséget von el környezetétől. Nagy melegben, fizikai munka és sport közben ezért izzadunk: a szervezet így tud megszabadulni a felesleges hőmennyiségtől. (Ugyanakkor szélben, vizesen veszélyesen ki lehet hűlni.)
−	[[Fájl:5002_Carnot-ciklus.jpg|bélyegkép|200px|2. ábra]]	+	==A hősugárzás==
−	Az 1-2 folyamat egy [http://en.wikipedia.org/wiki/Adiabatic_process adiabatikus] összenyomás. A külvilágtól hőszigeteléssel elválasztott gázt külső munkavégzéssel összenyomjuk – ennek hatására a belső energiája, és így a hőmérséklete is megnő.	+	===Nem csak izzó testeknél!===
		+	A [http://en.wikipedia.org/wiki/Thermal_radiation hősugárzás] az izzó testek estében (pl. napsütés, hősugárzó) nem csak a bőrünkkel érzékelhető, hanem látható is (hiszen ilyenkor az elektromágneses sugárzás egy része a látható fény tartományába esik). De nem csak a forró testek, hanem minden test sugároz! A sugárzás intenzitása azonban az abszolút hőmérséklet negyedik hatványával arányos, így a hidegebb testek sugárzása sokkal gyengébb. Ennek ellenére a hővezetés és a hőáramlás mellett a hősugárzásnak is fontos szerepe van a szobahőmérsékletű tárgyak közti hőcserében is. A környezetünkben minden test sugároz, és ugyanakkor el is nyel hősugárzást. Ezen a hőmérsékleten a hősugárzás az elektromágneses spektrum emberi szemmel nem látható, infravörös tartományába esik (erre a célra készített kamerákkal azonban [[#Hőmérsékletmérés színkép alapján|érzékelhető]]).
−	A 2-3 folyamat egy [http://en.wikipedia.org/wiki/Isothermal_process izoterm] kitágulás. A gáz a (legalább) $T_2$ hőmérsékletű környezettől („kazán”) hőt vesz fel, eközben kitágul, és munkát végez. A belső energiája (és így a hőmérséklete) nem változik, mert a felvett hő és a munkavégzés nagysága megegyezik.	+	===Az abszorpciós tényező, feketetest-sugárzás===
		+	A testek a rájuk eső hősugárzás egy részét elnyelik, a többit visszaverik (vagy átengedik). A beérkező sugárzás [[#A hősugárzás spektrális eloszlása|hullámhosszától]] is függő $a$ abszorpciós tényező megadja, hogy a test a ráeső hőáram mekkora részét nyeli el. A tökéletesen tükröző (vagy tökéletesen átlátszó) test abszorpciós tényezője $a$=0, a minden sugárzást elnyelő, „fekete” test abszorpciós tényezője pedig $a$=1. A „fekete” szó azért van idézőjelben, mert itt nem csak látható sugárzásról van szó: az infravörös tartományban egy látható tartományban „színes” test is lehet „fekete”.
−	A 3-4 folyamat egy adiabatikus kitágulás. A gáz ismét a külvilágtól elzárt (hőcsere nincs), a munkavégzés miatt csökken a belső energia és a hőmérséklet. Bebizonyítható, hogy a gáz munkavégzése éppen ugyanakkora, mint az 1-2 folyamatban a gázon végzett munka, így ez a két folyamat egymást kiegyenlíti, a további számításokból kihagyható. (Csak azért van rájuk szükség, hogy a gáz átjusson egyik izotermáról a másikra.)	+	A feketetest egy olyan (elvi szempontból is fontos) test, amely minden frekvencián minden hősugárzást elnyel, abszorpciós együtthatója hullámhossztól függetlenül $a$=1. (Valódi anyagok csak jó közelítéssel lehetnek ilyenek.)
−	A 4-1 folyamatban a gázt vissza kell juttatni a kiinduló állapotba, hogy a folyamat zárt, ciklikusan ismételhető legyen. Ez egy izoterm összenyomás: a gázt külső munkavégzéssel össze kell nyomni, miközben az így nyert belső energiát a (legfeljebb) $T_1$ hőmérsékletű környezetnek („hűtő”) leadja.	+	A feketetest sugárzásnak $j_Q$ intenzitása (a hőáramsűrűség) csak a test $T$ abszolút hőmérsékletétől függ ([http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_law Stefan-Boltzmann-törvény]): $$j_Q=\sigma T^4$$ ahol $$\sigma=5,67\cdot 10^{-8}\quad{\rm Wm}^{-2}{\rm K}^{-4}$$
−	A körfolyamat során a gáz a melegebb környezettől (a „kazán”-tól) felvesz $Q_2$ hőt, a hidegebb környezetnek (a „hűtő”-nek) pedig lead $Q_1$ hőt. A kettő különbsége a hőerőgép által végzett hasznos munka (a kitágulás közben végzett munka és az összenyomáshoz felhasznált munka különbsége): $$W=Q_2-Q_1$$ A folyamat hatásfoka a hasznos munka és a felvett hő hányadosa: $$\eta=\frac{W}{Q_2}=\frac{Q_2-Q_1}{Q_2}=1-\frac{Q_1}{Q_2}$$	+	a [http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_constant Stefan-Boltzmann-állandó].
−	hiszen a hűtőnek leadott energiát nem lehet a kazánban újra hasznosítani. Bebizonyítható, hogy a Carnot-ciklus esetében $$\frac{Q_1}{Q_2}=\frac{T_1}{T_2}$$ Ezzel az ideális Carnot-gép hatásfoka $$\eta=1-\frac{T_1}{T_2}$$	+	===Abszorpció és emisszió: miért fekete a hűtőborda?===
		+	Egy (nem fekete) test által kisugárzott hőáram $$J_Q=A\sigma e T^4$$
−	A fordított irányban működtetett Carnot-ciklus külső munka ($W$) hatására $Q_1$ hőt von el a hidegebb ($T_1$) hőmérsékletű környezettől, és $Q_2$ hőt ad le a melegebb ($T_2$) hőmérsékletű környezetnek. A magasabb hőmérsékleten leadott hő a hidegebb környezettől felvett hő és a befektetett munka összege: $$Q_2=Q_1+W$$	+	ahol $A$ a test sugárzó felülete, $e$ pedig az emissziós állandó. Ez az állandó adja meg, hogy az adott test mennyi hőt sugároz ki az ugyanekkora felületű és hőmérsékletű feketetesthez képest. (A feketetest emissziós állandója $e$=1.)
−	Ez a folyamat a hőszivattyú és a hűtőgép modellje (a valódi berendezések ennél bonyolultabb folyamatokkal működnek).	+	Az emissziós állandó (ami az abszorpciós állandóhoz hasonlóan hullámhosszfüggő) nem független az abszorpciós állandótól. Megmutatjuk, hogy minden testre $$e=a$$
−	Hőszivattyúval a külső (hidegebb) környezettől elvont hő felhasználásával lehet fűteni, így a berendezés teljesítménytényezője 1-nél nagyobb: $$\varepsilon=\frac{Q_2}{W}=\frac{Q_1+W}{W}=1+\frac{Q_1}{W}$$	+	azaz ugyanolyan körülmények között a „fekete” testek sugároznak a legerősebben, és a tükröző (vagy átlátszó) testek a leggyengébben. Emiatt festik a hűtőbordákat matt feketére: így tud leadni adott hőmérsékleten, adott felületen a lehető legtöbb hőt.
−	A hűtőgép hőt von el egy a környezeténél hidegebb helyről, és azt (a befektetett munkával együtt) leadja a melegebb környezetnek. Ezért meleg a hűtőgép hátulja.	+	Az állítás bizonyításához megmutatjuk, hogy ha nem lenne igaz, az ellentmondana a [[Rend és rendetlenség#A hőtan II. főtétele|II. főtételnek]].
−	===A II. főtétel néhány megfogalmazása===	+	[[Fájl:6001_emisszios_tenyezo.jpg|bélyegkép|200px|1. ábra]]
−	Az I. főtétel kimondja, hogy energia nem keletkezhet (és nem tűnhet el). Ezzel korlátozza a lehetséges folyamatok körét, például kizárja az [http://en.wikipedia.org/wiki/Perpetual_motion örökmozgó] – az elsőfajú perpetuum mobile, egy olyan berendezés, amely a környezettől elzárva folyamatosan energiát termel – létét. Ugyanakkor az I. főtétel semmit nem mond a lehetséges folyamatok irányát.	+	Legyen két párhuzamos felület minden mástól elszigetelve, és legyenek kezdetben azonos hőmérsékletűek. Egymás közt is csak hősugárzással cserélhetnek energiát. Legyen az egyik (a bal oldali) fekete ($a$=1), a másik aránylag jól tükröző (pl. $a$=0,3), ugyanakkor tegyük fel, hogy az állításunkkal ellentétben mindkettőnek mégis $e$=1 az emissziós tényezője. Az 1/a ábra alapján látható, hogy ekkor mindkét oldal ugyanakkora teljesítménnyel sugározna, viszont nem ugyanannyit nyelne el. (A részben tükröző test a beeső sugárzás nagyobb részét visszaveri, amit szintén a fekete test nyel el.) Ilyen módon a két kezdetben egyforma hőmérsékletű test közül az egyik külső hatás nélkül felmelegedne, a másik pedig lehűlne, ami ellentmondana a II. főtételnek. Az 1/b ábrán látható, hogy ha a részben tükröző test emissziós tényezője megegyezik az abszorpciós tényezőjével, akkor mind a két test összesen ugyanannyi energiát nyel el, mint amennyit kisugároz, és így a hőmérsékletek nem változnak.
−	A tapasztalat szerint viszont bizonyos folyamatok csak kitüntetett irányban mennek végre. Ha például forró vízbe jeget dobunk, akkor az „magától” elolvad, és langyos víz keletkezik. Ugyanakkor a magára hagyott langyos vízből nem lesz külső behatás nélkül újra jég és forró víz (annak ellenére, hogy az I. főtétel ezt nem tiltaná).	+	==A hősugárzás spektrális eloszlása==
		+	===Hőmérsékletmérés színkép alapján===
		+	A hősugárzás nem egy hullámhosszon, hanem a teljes elektromágneses spektrumon történik. A spektrális eloszlás azt adja meg, hogy a teljes kisugárzott energia hogyan oszlik el a különböző hullámhosszúságok között. A [http://en.wikipedia.org/wiki/Black_body feketetest-sugárzás] spektrális eloszlásának elméleti magyarázata a XIX. század végén még hiányzott. [http://en.wikipedia.org/wiki/Max_Planck Max Planck] 1900 karácsonyán csak az energiakvantum fogalmának bevezetésével tudta megmagyarázni a [http://en.wikipedia.org/wiki/Planck%27s_law sugárzási törvényt], ezzel elindítva a XX. századi fizika alapvető elméletét, a [http://en.wikipedia.org/wiki/Quantum_mechanics kvantummechanikát].
−	A [http://en.wikipedia.org/wiki/Second_law_of_thermodynamics termodinamika II. főtétele] a folyamatok irányát határozza meg. Sokféleképp megfogalmazható, ezek közül néhány (és majd [[#Az entrópia termodinamikai értelmezése, a II. főtétel megfogalmazása entrópiával|kicsit később]] egy további is):	+	A spektrum függ a sugárzó test hőmérsékletétől. Mint [[#Az abszorpciós tényező, feketetest-sugárzás|láttuk]], a teljes kisugárzott energia arányos az abszolút hőmérséklet negyedik hatványával. Emellett a hőmérséklet növelésével a spektrum a magasabb frekvenciák (kisebb hullámhosszok) felé tolódik. A [http://en.wikipedia.org/wiki/Wien%27s_displacement_law Wien-féle eltolódási törvény] szerint a maximális intenzitáshoz tartozó hullámhossz fordítva arányos az abszolút hőmérséklettel.
−	A hőátadás spontán (külső hatás nélkül) mindig a melegebb testről a hidegebb felé történik.	+	Szobahőmérsékleten a sugárzás gyakorlatilag teljesen a nem látható, infravörös tartományba esik. 550-600 °C hőmérséklet felett a test már sugároz annyit a látható tartományban is, hogy a szemünk érzékelje (vörös izzás). A Nap kb. 6000 K hőmérsékletű felületéről érkező napfényben a maximális intenzitás már a látható tartományba esik (a hullámhossza kb. 550 nm, zöld szín).
−	Az intenzív állapotjelzők különbségei (hőmérsékletkülönbség, nyomáskülönbség, kémiai potenciál különbség) idővel mindig a kiegyenlítődés felé változnak.	+	A sugárzás intenzitása és spektrális eloszlása alapján következtetni lehet a sugárzó test hőmérsékletére. (Természetesen figyelembe kell venni, hogy a valódi testek nem feketetestek.) A [http://en.wikipedia.org/wiki/Pyrometer pirométer] egy ilyen elven működő érintésmentes hőmérő, amivel nagyon nagy hőmérsékletek is mérhetők. A [http://en.wikipedia.org/wiki/Thermography termográfia] a fényképezéshez vagy a filmezéshez hasonló képalkotás az infravörös tartományban. A mesterségesen színezett képeken a színek a sugárzó test hőmérsékletét mutatják.
−	Egy (ciklikus folyamattal működő) hőerőgép termikus hatásfoka soha nem lehet 1, azaz egy rendszer belső energiája nem alakítható teljes egészében mechanikai munkává. (Nem készíthető [http://en.wikipedia.org/wiki/Perpetual_motion ''másodfajú'' perpetuum mobile] sem.) A valóságos hőerőgépek hatásfoka nem lehet jobb, mint a [[#Hőerőgép, hőszivattyú, hűtőgép|Carnot-gép]] termikus hatásfoka. Így $$\eta\leq 1-\frac{T_1}{T_2}<1$$	+	===Hősugárzás a természetben, hová verjük a sátrunkat?===
		+	Környezetünkben minden test sugároz, természetesen a saját testünk is. A hősugárzásról azonban elsősorban forró testek jutnak eszünkbe, például a napfény, vagy egy vörösen izzó hősugárzó. A szobahőmérsékletű testek sugárzását alig vesszük észre. Ugyanakkor, ha egy hideg betonfal, vagy jégtömb közelében áll valaki, akkor azt érzi, hogy a hideg testből „sugárzik a hideg”. Van „hideg sugárzás” is? Természetesen nincs. A testünkkel közel azonos hőmérsékletű testek sugárzását azért nem érezzük, mert ilyenkor a mi általunk kisugárzott energia és a test által felénk sugárzott energia éppen kiegyenlíti egymást. Ha a környező testek jóval hidegebbek a testünknél, akkor kevesebb sugárzó hő éri irányukból a bőrünket, mint amennyit kisugároz, így lehűl. Ezt érezzük úgy, hogy „sugárzik a hideg”.
−	ahol $T_1$ és $T_2$ a gép működéséhez használt hideg és meleg környezet („hőtartály”) hőmérséklete. A hőerőgép működtetéséhez két különböző hőmérsékletű hőtartály szükséges.	+	Ahhoz, hogy a testhőmérsékletünk állandó maradjon, a testünkben termelődő hőtől (nyugalmi állapotban kb. 50 W) folyamatosan meg kell szabadulnunk. Ezért a testhőmérsékletünknél kicsit hidegebb (20-25 °C-os) környezetben érezzük magunkat kellemesen. Ha a környezet ennél melegebb, akkor csak izzadás ([[#A hőátadás fokozása halmazállapot-változással|halmazállapot-változás]]) segítségével tudjuk leadni a felesleges hőt. Ha a környezet sokkal hidegebb, akkor fel kell öltöznünk: a hőszigetelő ruha felülete alacsonyabb hőmérsékletű a testünknél (hiszen ez a hőmérséklet-gradiens kell a hővezetéshez), így kevesebb hőt sugároz ki.
−	===Peltier-elem: a számítógépben használt hűtőgép===	+	A természetben a testünket a napsugárzás és a környező tárgyak sugárzása éri. A Napból érkező (elsősorban látható fényből és közeli infravörösből álló) sugárzás azonban térben és időben egyenetlenül éri a Földet. Nappal, tiszta időben kb. 1000 W/m<math>^2</math> teljesítmény ér a Föld felszínén egy napsugárzásra merőleges felületet. Ugyanakkor éjszaka csak a talaj, a környező tárgyak és a légkör sugároz felénk. A tiszta légkör azonban keveset nyel el (kicsi az abszorpciós együtthatója), és így keveset is sugároz (kicsi az emissziós együtthatója). Derült időben az égbolt így csak annyi energiát sugároz, mint egy nagyon hideg test. Ez okozza derült időben az eget „látó” felületek jelentős lehűlését. A környező levegőnél hidegebb tárgyakra pedig harmat vagy dér formájában kicsapódhat a levegő nedvességtartalma.
−	[[Fájl:5003_termoelem.jpg|bélyegkép|200px|3. ábra]]	+
−	Hőerőgépek és hűtőgépek nem csak gázok összenyomásával és kitágulásával működhetnek. A termoelektromos jelenségek lehetővé teszik mozgó alkatrésze nélküli, közvetlenül elektromos energiát termelő, illetve elektromos energiával működő eszközök készítését.	+
−	Két különböző fém, vagy különböző félvezető anyag érintkezésénél potenciálkülönbség alakul ki. Ez a potenciálkülönbség hőmérsékletfüggő, ezért ha a 3. ábrán látható elrendezésben a két érintkezési pont hőmérséklete különböző, a kimeneteken $U$ elektromos feszültség jelenik meg ([http://en.wikipedia.org/wiki/Thermoelectric_effect#Seebeck_effect Seebeck-effektus]). A feszültség arányos a két érintkezési pont hőmérsékletkülönbségével: $$U=\alpha\Delta T$$	+	Hová verjük a sátrunkat, ha éjjel nem akarunk fázni, és reggel szárazon szeretnénk elcsomagolni? Borult időben majdnem mindegy: ilyenkor a felhők visszaverik a Föld felszínéről kisugárzott sugárzást, és így az égbolt erősebben sugároz, nem lesz olyan erős kisugárzás, és az éjszaka melegebb lesz. Derült időben viszont fák alatt érdemes sátrazni: a fák lombja a környező levegővel azonos hőmérsékletű, így sokkal erősebben sugároz, mint a közel átlátszó derült égbolt. Derült nyári éjszakákon az erdőben szárazon és melegen lehet ébredni, míg a réteket vastag harmat borítja.
−	ahol $\alpha$ az anyagpárra jellemző Seebeck-együttható.	+	===Üvegházhatás===
		+	Az abszorpciós tényezőhöz hasonlóan a testek átlátszósága is hullámhosszfüggő. A sima üveg felület például átlátszó a látható tartományban, de az infravörös sugárzást visszaveri. Ezt a jelenséget használják ki a kertészek az üvegházak építésével: az üveglapok átengedik a napfényt, ami elnyelődik a talajban és a növényekben. A szobahőmérsékletű tárgyak hősugárzását viszont az üveg visszaveri, így az üvegház felmelegszik.
−	A jelenség jól használható hőmérsékletmérésre: ha az egyik érintkezési pont hőmérsékletét állandó értéken tartjuk (pl. olvadó jégben, vagy forrásban lévő cseppfolyós nitrogénben), akkor a Seebeck-együttható ismeretében a feszültség mérésével meghatározható a másik pont hőmérséklete.	+	A globális [http://en.wikipedia.org/wiki/Greenhouse_effect üvegházhatás] ugyanilyen elven alapul: a széndioxid, a metán (és kis mértékben a vízgőz is) a látható fényben átlátszók, míg az infra tartományban elnyelik és részben visszaverik a sugárzást. A Földnek, ahhoz hogy ne változzon a hőmérséklete, folyamatosan ki kell sugároznia azt az energiát, amit a Naptól kap (és ami a Föld belsejében radioaktív bomlásokból keletkezik). Ha a légkör kevésbé átlátszó az infravörös tartományban, akkor a felszíni hőmérsékletnek magasabbnak kell lennie ugyanolyan erős kisugárzáshoz.
−	Ha a kimenetet egy ellenállással terheljük, akkor az áramkörben $I$ áram fog folyni. Az érintkezési pontokon átfolyó áram egy másik termoelektromos jelenség, a [http://en.wikipedia.org/wiki/Thermoelectric_effect#Peltier_effect Peltier-effektus] következtében a meleg érintkezési pontot hűteni, a hideg pontot pedig melegíteni fogja. Az elnyelődő, illetve felszabaduló hőteljesítmény $$\frac{{\rm d}Q}{{\rm d}t}=\pi I=\alpha TI$$	+	Az üvegházhatás jelentős része természetes eredetű. A legnagyobb részéért a kis mértékben üvegházhatású, de nagyon nagy mennyiségben jelenlévő vízgőz felelős. Ezen kívül természetes úton kerül széndioxid és metán is a légkörbe. Üvegházhatás nélkül a Földön túl hideg lenne.
−	ahol $\pi=\alpha T$ a az adott érintkezési pont abszolút hőmérsékletével arányos Peltier-együttható, $\alpha$ pedig a Seebeck-együttható.	+	A Föld két különböző visszacsatolási mechanizmussal is képes szabályozni a légköri széndioxid mennyiségét:
−	Ha ezeket a pontokat folyamatosan melegen ill. hidegen tartjuk, akkor egy közvetlenül elektromos energiát termelő hőerőgépet kapunk. A hatásfoka ugyan kicsi, de speciális körülmények között mégis célszerű a használata. Ilyen eszköz a [http://en.wikipedia.org/wiki/Radioisotope_thermoelectric_generator radioizotópos termoelektromos generátor], ahol a meleg oldal fűtését az eszközben elhelyezett közepesen hosszú felezési idejű radioaktív izotópok bomlása biztosítja. Ezt az elektromos energiaforrást elsősorban olyan űreszközökben használják, amelyekben az energiaellátás napelemekkel nem megoldható (pl. a Naprendszer távoli részeiben).	+	A (nagyon lassú) geológiai szabályozás lényege, hogy ha nagyon sok a széndioxid a légkörben, akkor felmelegedés következik be. A meleg tengervízben feloldódó széndioxid reagál a szilikátokkal, és karbonátos kőzetekben megköti a felesleges széndioxidot. Ha túl kevés a széndioxid a légkörben, akkor megindul az eljegesedés, a jégtakarók súlya a magmába nyomja a karbonátos kőzeteket, ahol a széndioxid vulkáni tevékenységgel újra a légkörbe jut.
−	Ha az eszközre külső feszültségforrásból kapcsolunk áramot, akkor hűtőgépként (hőszivattyúként) fog működni: a befektetett elektromos energia segítségével az egyik (hidegebb) érintkezési pontból hőt von el, a másikon pedig hőt szabadít fel. A gyakorlatban használt [http://en.wikipedia.org/wiki/Thermoelectric_cooling Peltier-elemekben] különböző adalékolású (n- és p-típusú) félvezetőkből készülő termopárok vannak elektromosan sorba, míg hőtani szempontból párhuzamosan kapcsolva. Ha a fűtött oldalon felszabaduló hőt hűtőbordákkal, szellőztetéssel vagy vízhűtéssel elvezetjük, akkor a hűtött oldal a környezetnél jóval alacsonyabb hőmérsékletre hűthető. A hűtés hatékonyságát azonban a Peltier-elemben felszabaduló Joule-hő és a hővezetés is korlátozza.	+	A (kicsit gyorsabb) biológiai szabályozás a növények széndioxid megkötésén alapul. A magas széndioxid-koncentráció okozta meleg éghajlaton intenzívebb a növényi élet, és a széndioxid az élő növényekben és a növényi maradványokban (szén, kőolaj, földgáz) megkötődik. A légköri széndioxid-koncentráció csökkenése lehűlést és a növényzet visszaszorulását eredményezi, így a megkötött széndioxid részben visszajut a légkörbe.
−	Az eszközt széles körben használják számítógép alkatrészek és más elektromos berendezések hűtésére, valamint hordozható (kis egyenfeszültségről működtethető) hűtőgépekhez.	+	A fosszilis energiahordozók elégetése és a növényzet irtása azonban a légköri széndioxid-koncentráció földtörténeti léptékben nagyon gyors növekedését okozza, ami a természetes változásokhoz képest túl gyors felmelegedést okozhat. Sokak szerint ez ma a legsúlyosabb környezeti veszély.
−	===Az entrópia termodinamikai értelmezése, a II. főtétel megfogalmazása entrópiával===	+	==Hűtés-fűtés==
−	A belső energia egy (extenzív) ''állapotjelző'', ezért két állapot közötti megváltozása független attól, hogy milyen folyamatokkal jutott a rendszer az egyik állapotból a másikba. A belső energia kétféleképpen változhat: hőközléssel és munkavégzéssel. A rendszer által felvett hő függ attól, hogy milyen folyamattal jutott a rendszer az egyik állapotból a másikba (épp ezt használják ki a ciklikus folyamatokkal működő gépek), ezért a felvett hő nem állapotjelző.	+	===Egy lakás hőháztartása===
		+	Az energiaárak növekedésével egyre inkább előtérbe kerül a lakóházak hőszigetelése. Érdemes áttekinteni egy lakás teljes hőháztartását!
−	[http://en.wikipedia.org/wiki/Rudolf_Clausius Clausius] bevezetett egy olyan mennyiséget, az [http://en.wikipedia.org/wiki/Entropy entrópiát], amely szoros kapcsolatban van a hőközléssel, de ugyanakkor állapotjelző. A  [http://en.wikipedia.org/wiki/Entropy_(classical_thermodynamics) klasszikus] termodinamikában az $S$ entrópia megváltozása definiálható, reverzibilis (megfordítható) folyamatoknál : $${\rm d}S=\frac{\delta Q}{T}$$	+	A lakásba bejutó energia meghatározásakor a fűtésen kívül figyelembe kell venni az ablakokon keresztül bejutó napfényt (ami megfelelő tájolás esetében télen se elhanyagolható – nyáron viszont árnyékolással csökkenthető), a lakásban működő háztartási eszközök hőleadását (a berendezések – hűtőgép, hajszárító, számítógép, tévé, belső világítás stb. – elektromos fogyasztása végül hővé alakul), és a lakásban élő emberek hőtermelését is. Ezen kívül nyáron (amikor kint melegebb van, mint a lakásban) hővezetéssel a falakon és nyílászárókon át is befelé áramlik az energia.
−	A kifejezésben $T$ az abszolút hőmérséklet, az elemi hőközlésben használt $\delta$ jel (a ${\rm d}$ helyett) arra utal, hogy $Q$ nem állapotjelző.	+	A lakás belsejéből télen (amikor a kint hidegebb van, mint a lakásban) a falakon és a nyílászárókon keresztül hővezetéssel jut ki az energia. Ezen belül hagyományos épületeknél meghatározó a nyílászárók és a rossz tervezés vagy kivitelezés miatt kialakuló hőhidak (például a hőszigetelésen átvezető vasbeton szerkezetek) szerepe. Jelentős energiaveszteséget okoz a rosszul záródó ablakoknál kialakuló folyamatos légáramlás, a kéményeken keresztül távozó meleg füst és levegő, valamint a szellőzés is. Nyári hőségben klímaberendezéssel lehet mesterségesen elvonni hőt a lakásból.
−	Reverzibilis folyamatokban a $$\Delta S=\int_1^2{\rm d}S=\int_1^2\frac{\delta Q}{T}$$ integrál független a választott folyamattól, azaz az entrópia állapotjelző.	+	A kinti hőmérsékletnek – különösen nyáron – jelentős napi ingadozása van. Ezért fontos a ház hőkapacitása is: a vastag, nagy tömegű falakban tárolt energia csökkenti a lakásban a napi hőmérsékletingadozást.
−	A definíció csak az entrópia megváltozását határozza meg, egy egyelőre szabadon választott kezdőértékhez viszonyítva. (Az entrópia abszolút értékét a [http://en.wikipedia.org/wiki/Third_Law_of_Thermodynamics termodinamika III. főtétele] segítségével lehet meghatározni.) Az entrópia mértékegysége J/K.	+	Az épület alakja és tájolása is jelentősen befolyásolja a hőháztartást. Ugyanahhoz az alapterülethez egy kompakt, nagyjából kocka alakú épület esetében tartozik a legkisebb hőleadó felület. Ugyanakkor a téli besugárzás jobb kihasználásához ettől eltérő (kb. 1:1,6) oldalarányú épület az optimális, természetesen megfelelő [http://en.wikipedia.org/wiki/Passive_solar_design tájolással].
−	Irreverzibilis (nem megfordítható) folyamatokban az entrópia megváltozása $$\Delta S\geq\int\frac{\delta Q}{T}$$ Ebből következik, hogy ha nincs hőközlés, akkor az entrópia megváltozása csak pozitív lehet: $$Q=0\Rightarrow\Delta S\geq 0$$	+	A szinte semmi külső energiát nem igénylő épületek világszerte használt német szabványa a [http://en.wikipedia.org/wiki/Passive_house passzívház]. Az ilyen épületek évente legfeljebb 15 kW/m<math>^2</math> energiát használnak fűtésre-hűtésre. Az ilyen épületekben a vastag (50 cm), jó hőszigetelésű falakkal, a hézagmentes, háromrétegű, nemesgáztöltésű nyílászárókkal, valamint hőhídmentes konstrukcióval minimálisra csökkentik a hőveszteséget. A szellőzést a talajban kígyózó csővezetéken keresztül beáramló levegővel biztosítják: a talajban hosszan kanyargó csőben télen melegszik, nyáron lehűl a levegő. Ezután télen a házból kilépő levegő melegíti tovább egy hőcserélőben. A minimális veszteséget a megfelelő tájolásnak köszönhető besugárzás, és a házban lakó emberek, valamint a háztartási eszközök hőkibocsátása biztosítja. A használati meleg vizet napkollektorok melegítik, a nyári hűtést a talajban előhűtött levegő és megfelelő árnyékolás biztosítja. Gázbekötés, kémény nincsen. Az első [http://hu.wikipedia.org/wiki/Passz%C3%ADvh%C3%A1z#K.C3.A9m.C3.A9ny_.C3.A9s_g.C3.A1zbek.C3.B6t.C3.A9s_n.C3.A9lk.C3.BCl magyar] passzívház Szadán épült.
−	Azaz ''zárt rendszer'' entrópiája nem csökkenhet. Ez a II. főtétel újabb megfogalmazása.	+	Az elektromos energia részben vagy egészében napelemekkel, vagy egyéb megújuló energiaforrásokkal is előállítható. Léteznek már pozitív energiamérlegű [http://en.wikipedia.org/wiki/Energy-plus-house aktív házak], melyek egy év alatt több energiát termelnek (és juttatnak vissza az elektromos hálózatba), mint amennyit felhasználnak.
−		+
−	Ahogy [[#A II. főtétel néhány megfogalmazása|láttuk]], a tapasztalat szerint egy magára hagyott rendszerben a kezdeti hőmérséklet-, nyomás- és kémiai potenciál különbségek idővel kiegyenlítődnek. A kezdeti „rendezettség” (pl. forró és hideg víz, kis és nagy nyomás, szétválasztott komponensek) idővel irreverzibilisen (megfordíthatatlanul) a „rendezetlenség” (langyos víz, kiegyenlített nyomás, összekeveredett komponensek) irányába halad. Eközben viszont nő az entrópiája. Eszerint a (klasszikus termodinamikában szemléletes jelentés nélküli) entrópiát nevezhetjük a „rendezetlenség mértékének”.	+
−		+
−	Az entrópia [http://en.wikipedia.org/wiki/Entropy_(statistical_thermodynamics) statisztikus értelmezése] alátámasztja ezt a megállapítást. A makroszkopikus állapotjelzők meghatározzák a rendszer egy ''makroállapot''át. Ugyanakkor egy makroállapotot nagyon sok különböző ''mikroállapot'' valósíthat meg, ahol egy mikroállapot a rendszer részecskéinek egy adott konfigurációja a hely- és sebességkoordinátákból álló fázistérben. Ha egy makroállapotot $Z$ számú mikroállapot valósíthat meg, akkor a rendszer entrópiája $$S=k\ln Z$$	+
−		+
−	ahol $k$ a [http://en.wikipedia.org/wiki/Boltzmann_constant Boltzmann-állandó]. (Egy adott makroállapothoz tartozó mikroállapotok leszámolása nem könnyű, és a klasszikus fizikában [http://en.wikipedia.org/wiki/Gibbs_paradox ellentmondásokra] is juthatunk. A megoldást kvantumstatisztikák jelentik.) Kombinatorikai megfontolásokkal könnyen belátható, hogy „rendezetlen” makroállapotokat sokkal több mikroállapot valósít meg, és így a hozzá tartozó entrópia is nagyobb.	+
−		+
−	==Információ és entrópia==	+
−	===A Maxwell-démon és néhány híres feloldási kísérlete===	+
−	[[Fájl:5004_Maxwell-demon.jpg|bélyegkép|200px|4. ábra]]	+
−	A [http://en.wikipedia.org/wiki/Maxwell%27s_demon Maxwell-démon] egy híres gondolatkísérlet szereplője. A [http://en.wikipedia.org/wiki/James_Clerk_Maxwell Maxwell] által felvetett gondolatkísérletben egy gáztartályt hőszigetelő fallal kettéosztunk, amin egy kicsiny nyitható-csukható ajtó van. Egy apró lény (ő a „démon”) az ajtót attól függően nyitja vagy csukja, hogy melyik irányból milyen sebességű molekula érkezik. Ha az átlagosnál gyorsabb molekulákat pl. csak balról jobbra engedi át, akkor az eredetileg azonos hőmérsékletű két fél közül a jobboldali – külső hatás nélkül – felmelegszik, míg a baloldali lehűl. Ezzel egy zárt rendszer entrópiája csökkenne, ami viszont ellentmond a termodinamika II. főtételének.	+
−		+
−	A paradoxon feloldására sok kísérlet született, az egyik [http://hu.wikipedia.org/wiki/Szil%C3%A1rd_Le%C3%B3 Szilárd Leó] gondolatmenete. Egy „valódi” démonnak valahogy meg kell mérnie a molekulák sebességét (a méréshez például egy apró zseblámpával meg kell világítania a molekulákat). Ehhez a démonnak energiát kell felhasználnia, ami viszont megnöveli az entrópiáját. A démon entrópianövekedése nagyobb, mint a gáz entrópiacsökkenése, így az egész rendszer (gáz + démon) entrópiája nem fog csökkenni.	+
−		+
−	[http://en.wikipedia.org/wiki/Rolf_Landauer Landauer] ellenvetése szerint viszont a mérési folyamatnak nem feltétlenül kell növelnie a rendszer entrópiáját, ha a folyamat reverzibilis (megfordítható). A reverzibilitáshoz viszont a démonnak minden mérési adatot fel kell jegyeznie, és meg kell őriznie. A memóriakapacitása nem lehet vételen, ezért előbb-utóbb törölnie kell a régebbi mérési adatokat, ami viszont a mérést irreverzibilissé (meg nem fordíthatóvá) teszi. Az irreverzibilis folyamat viszont entrópianövekedéssel jár, tehát az információ törlése növeli a rendszer entrópiáját. 1 bit információ törlése $$\Delta S\geq k\ln 2$$ entrópianövekedéssel, és így $$Q\geq kT\ln 2$$ hőfelszabadulással jár.	+
−		+
−	A Maxwell-démontól így eljutottunk az [http://en.wikipedia.org/wiki/Entropy_(information_theory) információs entrópia] fogalmához. Az [http://en.wikipedia.org/wiki/Information_theory információelméletben] az entrópia egy üzenet bizonytalanságát, azaz várható információtartalmát méri. Egy előre ismert, pl. csupa azonos karakterből álló üzenet bizonytalansága – és így információtartalma nulla. Egy véletlenszerű karaktersorozatnak viszont maximális az információtartalma, és így az entrópiája is.	+
−		+
−	==A zaj==	+
−	===A zaj jellemzése, néhány oka===	+
−	A [http://en.wikipedia.org/wiki/Noise zaj] a mért jelre, továbbított információtartalomra különböző okokból „rárakódó” zavar. A zaj eredetileg az akusztikában használt fogalom, de általánosabb értelemben bármely (elektromos, optikai, stb.) analóg vagy digitális jelnél fellépő véletlenszerű ingadozás zaj.	+
−		+
−	Analóg jeleknél a zaj a spektrumával jellemezhető. A [http://en.wikipedia.org/wiki/White_noise fehérzajban] a jel intenzitása a vizsgált tartományban minden frekvencián egyforma, az [http://en.wikipedia.org/wiki/Pink_noise 1/f zaj] spektrális intenzitása pedig fordítva arányos a frekvenciával.	+
−		+
−	A zajnak nagyon sok oka lehet. Az elektromos jelekben mindig fellépő a [http://en.wikipedia.org/wiki/Johnson-Nyquist_noise termikus zaj] a töltéshordozók hőmozgásából adódik. A p-n átmenetekben fellépő [http://en.wikipedia.org/wiki/Shot_noise sörétzajt] pedig az elektromos töltés kvantáltsága okozza: az átmeneten időegységenként átlépő töltéshordozók száma fluktuál.	+
−		+
−	===Az információ kinyerése erősen zajos jelekből: a Hold-radar kísérlet===	+
−	A II. világháborúban új technika született: a [http://en.wikipedia.org/wiki/Radar radar]. A háború alatt az Egyesült Izzóban is folytak radarfejlesztések. A háború végén felmerült a lehetősége, hogy a földi tárgyakról visszaverődő radarjelekhez hasonlóan a Holdról visszaverődő jeleket is detektálni lehet. A fő nehézséget az okozza, hogy a Hold nagy távolsága miatt a visszaverődő jel sok nagyságrenddel gyengébb, és így a [http://en.wikipedia.org/wiki/Signal-to-noise_ratio jel-zaj viszony] is sokkal kisebb, mint a földi célpontok esetében.	+
−		+
−	A berendezések tökéletesítésével, 0,05 s hosszú impulzusokkal és 20 Hz sávszélességű vevővel a jel-zaj viszonyt a kor technikájával legfeljebb 1/10-re lehetett javítani – ez azt jelenti, hogy a jelek még mindig egy nagyságrenddel kisebbek a zajnál. A megoldást az jelentette, hogy a kibocsátott jeleket periodikusan ismételték, és a beérkező jeleket összegezték. A zaj az összegzés során részben kiátlagolódik, a jel viszont folyamatosan növekszik, így kellően hosszú összegzés után a jel érzékelhetően a zaj fölé nő.	+
−		+
−	A méréstechnikában ma már széles körben használt [http://en.wikipedia.org/wiki/Lock-in_amplifier lock-in erősítők] ugyanezen elven alapulnak, de akkoriban még sokkal nehezebb volt ötlet gyakorlati megvalósítása. A jel N impulzus összegzésekor $N$-szeresére nő, a zaj viszont csak $\sqrt{N}$-szeresére, így a jel-zaj viszony is $\sqrt{N}$-szeresére javul. A Holdról kb. 2,5 másodperc alatt érkeznek vissza a radarhullámok, így 3 másodpercenként lehetett a jeleket kibocsátani. 1000 impulzus kibocsátása (a jel-zaj viszony kb. 30-szoros javítása) 50 percig tart. Akkoriban nem volt olyan elektromos eszköz, amivel a jeleket ilyen hosszú ideig lehetett összegezni.	+
−		+
−	Összegzésre az elektrolízist használták: az elbontott víz mennyisége – amit egy vékony csőben a folyadékszint eltolódásából lehetett leolvasni – arányos az áram integráljával. A vevő felerősített jelét 0,3 másodperces késleltetéssel 10 egymás utáni csövecskéhez kapcsolták. Ugyanez a mechanikus kapcsoló indította 3 másodpercenként a kibocsátott jeleket is, így az egyes csövecskékhez meghatározott időkésleltetés kapcsolódott. A Holdról visszaverődött jel így mindig ugyanabban a csövecskében bontotta a vizet, a többi csőben fejlődő gáz viszont csak a zajt mérte.	+
−		+
−	Előzetes számítások és a háborús viszontagságok után [http://hu.wikipedia.org/wiki/Bay_Zolt%C3%A1n Bay Zoltán] vezetésével 1945 nyarán kezdték építeni azt a berendezést, amellyel végül 1946. február 6-án – a sokkal jobb eszközökkel dolgozó amerikaiak után néhány héttel, a világon másodikként – sikerült detektálni a Holdról visszaverődő radarjeleket: a megfelelő csövecskében a folyadékszint egyértelműen a többi fölé emelkedett.	+
−		+
−	A kísérletből kiderült, hogy a radar 2,5 m hullámhosszú jele átjut a légkörön, és kijut a világűrbe, a Hold visszaverőképessége pedig kb. 1/10 ezen a hullámhosszon. A kísérlet a világűrkutatás új, „aktív” korszakát nyitotta meg.	+
−		+
−	==Zaj és önszerveződés==	+
−	===Szegregáció és mintázatképződés granulált anyagoknál===	+
−	[[Fájl:5005_szegregacio.jpg|bélyegkép|200px|5. ábra]]	+
−	A [http://en.wikipedia.org/wiki/Granular_material granulált anyagok] különböző alakú és méretű szemcsékből állnak. A szemcsék nagysága a mikrométeres mérettől (pl. festékporok) a  több méteresig (pl. sziklagörgetegek) terjedhet. Alakja lehet sima felületű gömb vagy szögletes, szabálytalan formájú szemcse. Tipikus, jól ismert, és gyakran vizsgált granulált anyag a homok.	+
−		+
−	A granulált anyagok viselkedése sok furcsaságot mutat. Folyadékokhoz hasonlóan önthetők, de ugyanakkor a kiöntött anyag nem terül szét teljesen, hanem egy anyagra jellemző rézsűszögű kupacot alkot. Még különösebben viselkednek a granulált anyagok keverékei: rázás, mozgatás, kiöntés hatására a várakozásokkal ellentétben nem összekeverednek, hanem szétválnak. Ez a spontán [http://en.wikipedia.org/wiki/Particle_segregation szegregáció] jelensége. Az 5. ábrán párhuzamos falak közé öntött mák-homok keverék látható. Az egyes rétegek véletlenszerű fluktuációk hatására meginduló kis lavinák hatására alakulnak ki.	+
−		+
−	[[Fájl:5006_granulalt_mintazatkepzodes.jpg|bélyegkép|200px|6. ábra]]	+
−	Egy másik meglepő jelenség a granulált anyagok rázásakor megfigyelhető mintázatképződés. Ha egy hengeres edénybe öntött vékony réteg homokot, vagy más granulált anyagot függőleges irányban rázni kezdünk, akkor az edény $g$-nél nagyobb maximális gyorsulása esetén a szemcsék ugrálni kezdenek, az ugráló részecskék pedig egymással és az edény aljával ütköznek. Azt várnánk, hogy a sok véletlenszerű ütközésből egy teljesen rendezetlen mozgás alakul ki, azonban az anyag különböző – a frekvenciától és a maximális gyorsulástól függő – mintázatokat alakít ki. A 6. ábrán három különböző mintázat látható, melyek 0,15 mm átmérőjű üveggyöngyök rázásakor alakultak ki. Bizonyos körülmények között a rezgetett rétegben hosszabb ideig stabil, lokalizált hullámok un. [http://en.wikipedia.org/wiki/Oscillon oszcillonok] is kialakulhatnak.	+
−		+
−	===Fraktálok===	+
−	A kristályok növekedése a magképződéssel ([http://en.wikipedia.org/wiki/Nucleation nukleáció]) kezdődik, majd ezt követi a kristályszemcse növekedése. A növekedési sebességet a lokális hőmérséklet és koncentráció befolyásolja, amelyekre viszont visszahat a kristályosodás. Emiatt a kristály növekedési sebessége erősen helyfüggő lesz, és a véletlen fluktuációk (zajok) hatására kialakuló kis „dudorok” sokkal gyorsabban nőnek. Ezeken a gyorsan növő részeken újabb véletlen fluktuációk hatására elágazások alakulnak ki, amely végül egy [http://en.wikipedia.org/wiki/Dendrite_(crystal) faágakra emlékeztető] kristály kialakulásához vezet. A jelenség [http://en.wikipedia.org/wiki/Snowflake hókristályok] és a [http://en.wikipedia.org/wiki/Frost zúzmara] kialakulásakor is megfigyelhető.	+
−		+
−	A kialakuló forma [http://en.wikipedia.org/wiki/Fractal fraktálos] szerkezetet mutat: azaz a kristály egyre kisebb méretekben ismétlődő önhasonló formákból épül fel.	+
−		+
−	===Kollektív mozgások, közlekedési dugók===	+
−	Izgalmas határtudomány a madár- és halrajok vagy tömegből menekülő emberek [http://en.wikipedia.org/wiki/Swarm_behaviour kollektív mozgásának] vizsgálata. A számítógépes modellek szerint ezek a látszólag nagyon bonyolult mozgások három egyszerű elv hatására alakulnak ki: minden egyed lehetőleg ugyanarra akar haladni, mint a szomszédai; mindegyik a szomszédai közelében akar maradni; de az összeütközést el akarja kerülni.	+
−		+
−	A kicsiny fluktuációk felerősödése jól megfigyelhető a közlekedésben is: az autópályákon kialakuló közlekedési dugókban gyakran megfigyelhető, hogy az autóoszlop többé-kevésbé periodikusan teljesen megáll, majd aránylag gyorsan mozog. A teljesen telített úton egyetlen véletlen fékezés is fékezések egész sorát okozhatja, amitől akár teljesen leáll a forgalom. Az így lelassuló autók előtt viszont üres útszakasz alakul ki, tehát a meginduló autók hirtelen sokkal gyorsabban haladhatnak – egészen addig, amíg utol nem érik a lassabb kocsioszlopot. Ez újabb fékezésekhez, és a folyamat ismétlődéséhez vezethet.	+
	----		----
−	Vissza a [[Fizika I.]] nyitóoldalára	+	Vissza a [[Fizika 1i - Mérnök informatikus alapszak|Fizika 1i]] nyitóoldalára
	1. [[Tér és idő]]		1. [[Tér és idő]]
209. sor:		162. sor:
	4. [[Rezgések]]		4. [[Rezgések]]
−	6. [[Hideg-meleg]]	+	5. [[Rend és rendetlenség]]
		+
		+	6. '''Hideg-meleg'''
	</wlatex>		</wlatex>

---

A lap jelenlegi, 2011. május 12., 15:55-kori változata

A komfort érzetünk egyik fontos tényezője hogy télen a meleg szobát, nyáron a hűvös, árnyas helyeket keressük. A „hideg és a meleg” iránti vágyunk kielégítése pénzbe kerül. Télen fűtűnk, nyáron hűtünk. De a technika világában a „melegedés” igen káros is lehet. Egy számítógép belsejében a hő mindig termelődik, így a processzor hűtése létfontosságú a berendezés megbízható működéséhez.

A hőátadási folyamatok fizikai alapjait jól ismerjük. Fel- és kihasználásuk a mérnöki munka egyik igen fontos területe. Hol termelni, hol „megszüntetni” akarjuk. A célt mindig az elérni kívánt eredmény határozza meg.

Tartalomjegyzék 1 Hőfelszabadulás 1.1 Hőfelszabadulás számítógépekben és élő szervezetekben 1.2 A hőátadás módjai 2 A hővezetés 2.1 A hővezetés törvényei 2.2 Különleges hőszigetelő anyagok 3 A hőáramlás 3.1 Gravitációs áramlások 3.2 Kényszerített áramlások 3.3 A hőátadás fokozása halmazállapot-változással 4 A hősugárzás 4.1 Nem csak izzó testeknél! 4.2 Az abszorpciós tényező, feketetest-sugárzás 4.3 Abszorpció és emisszió: miért fekete a hűtőborda? 5 A hősugárzás spektrális eloszlása 5.1 Hőmérsékletmérés színkép alapján 5.2 Hősugárzás a természetben, hová verjük a sátrunkat? 5.3 Üvegházhatás 6 Hűtés-fűtés 6.1 Egy lakás hőháztartása

Hőfelszabadulás

Hőfelszabadulás számítógépekben és élő szervezetekben

A számítógépekben (és más berendezésekben), valamint élő szervezetekben is folyamatosan hő szabadul fel, azaz külső vagy belső energiaforrások növelik a gép vagy az élő szervezet egyes részeinek belső energiáját. A hőfelszabadulásnak nagyon sokféle oka lehet.

Az élő szervezetekben az izmok munkavégzéséhez szükséges energiát a táplálékkal felvett szerves anyagok kémiai oxidációja fedezi. Ilyen szempontból az élő szervezet lényegében egy hőerőgép, amelyre természetesen igaz a II. főtétel: termikus hatásfoka egynél kisebb. Ezért a munkavégzéssel együtt szükségszerűen hőfelszabadulás jár. (Ugyanez az oka a belsőégésű motorral üzemelő járművekben felszabaduló hő döntő többségének is.) Ez a felszabaduló hő pótolja a szervezet hőleadását, és így képes a melegvérű állatokat (és az embert) állandó, a környezeténél általában magasabb hőmérsékleten tartani. Az állandó hőmérséklet megtartásához azonban a hőtermelést és a hőleadást egyensúlyban kell tartani.

A számítógépekben nincs hőerőgép, de például a mozgó alkatrészek súrlódása, az áramjárta vezetékekben felszabaduló Joule-hő, a mágneses anyagok (adathordozók, transzformátorok) hiszterézise folyamatosan hőt „termel”. A hőfelszabadulás aránylag kis méretű alkatrészekben (pl. a processzorban vagy a merevlemez író-olvasó fejében) különösen koncentráltan történik, és így ezek hűtésére különösen figyelni kell.

A hőátadás módjai

A termodinamika II. főtétele szerint a hőátadás mindig a melegebb testről a hidegebb irányába történik. A folyamat azonban több, lényegesen különböző módon történhet:

A hővezetés elsősorban szilárd testeken belül meghatározó folyamat. (Folyadékokban és gázokban csak akkor figyelhető meg önmagában, ha nem jöhet létre áramlás.) A rezgő atomok és molekulák közötti kölcsönhatás eredményeképpen a gyorsabban rezgő részecskék átlagosan több mozgási energiát adnak át a lassabb részecskéknek, mint viszont. Az energiatranszport tehát a hővezetésnél nem jár részecsketranszporttal.

A hőáramlás folyadékokban és gázokban lehetséges. Ekkor a hőátadás úgy történik, hogy az átlagosan nagyobb energiájú részecskék áramlással a melegebb helyről a hidegebb helyre kerülnek (míg az átlagosan kisebb energiájúak éppen fordítva, a hidegebb helyről a melegebb helyre áramlanak). Itt tehát az energiatranszport a részecsketranszporttal együtt történik.

Az előzőektől teljesen eltérő folyamat a hősugárzás, amikor a testek közti hőátadás elektromágneses sugárzás segítségével jön létre. Az elektromágneses hullámok vákuumban is terjednek, a világűrben csak így lehetséges hőátadás. Ugyanakkor a hősugárzásnak a földi folyamatokban is nagyon fontos szerepe van.

A hővezetés

A hővezetés törvényei

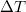A hőáram az időegység alatt szállított hő: A tapasztalat szerint egy homogén, állandó keresztmetszetű rúdban (vagy egy homogén falon keresztül) a hőáram egyenesen arányos a rúd két vége (illetve a fal két oldala) közti hőmérséklet-különbséggel valamint a rúd keresztmetszetével (a fal felületével), és fordítva arányos a rúd hosszával (a fal vastagságával):

A hővezetési tényező az anyagra jellemző állandó.

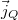Általános esetben a hővezetés a hőáramsűrűség-vektorral (az egységnyi felületen áthaladó hőáram) jellemezhető. A hőáramsűrűség egyenesen arányos a hőmérséklet-gradienssel (Fourier-törvény): Észrevehető, hogy az összefüggés analóg az elektromos vezetés Ohm-törvényével. Az keresztmetszetű, hosszúságú vezetőn folyó áramerősség (időegység alatt szállított töltés): ahol , a feszültség (potenciálkülönbség), és a fajlagos vezetőképesség (a fajlagos ellenállás reciproka). Differenciálisan pedig

ahol 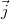az áramsűrűség-vektor, 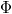az elektromos potenciál és 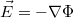az elektromos térerősség.

Az analógia lehetővé teszi összetett hővezetési problémák elektromos modellezését: ellenállásokat bekötni, feszültségeket és áramerősségeket mérni sokkal egyszerűbb, mint hővezető szerkezeteket megépíteni, hőmérsékleteket és hőáramokat mérni.

A legjobb hővezetők egyben jó elektromos vezetők is (ezüst, vörösréz, alumínium), aminek az az oka, hogy a szabad elektronoknak nemcsak az elektromos vezetésben, hanem a hővezetésben is fontos szerepük van.

Különleges hőszigetelő anyagok

Legjobb hőszigetelő a vákuum: azon keresztül csak hősugárzással lehet hőcsere. Így „működik” az acél termosz: a két, egymáshoz közeli, vékony fal közti levegőt kiszívják. (A falak közti hősugárzást pedig fényes, tükröző felületekkel csökkentik.)

A gázok is elég jó szigetelők lennének, ha nem alakulnának ki áramlások. A lyukacsos, porózus szerkezetekben az egymástól elzárt (és így az áramlásban akadályozott) levegőrétegek szigetelnek.

Az űrsiklók burkolására olyan speciális kerámiát fejlesztettek ki, amely kellő szilárdságú, és ugyanakkor nagyon jó hőszigetelő. (A légkörbe való belépéskor a nagyon nagy sebesség miatt az űrsikló felülete felforrósodik.) Ez az anyag olyan rossz hővezető, hogy ha vörösen izzik, akkor is kézbe lehet venni: A bőrünk lehűti a kerámia felületét, és az nem melegszik fel újra a rossz hővezetés miatt. (Ugyanezért nem éget a szauna 100 °C-os fa burkolata sem, pedig az ugyanilyen meleg víz, vagy fém tárgyak már égési sérülést okoznak.)

A hőáramlás

Gravitációs áramlások

A folyadékok és gázok sűrűsége függ a hőmérséklettől: általában a hőmérséklet növelésével csökken. (Kivétel pl. a víz 0 °C és 4 °C között.) Emiatt ha egy folyadék vagy gáz alját melegítjük (vagy tetejét hűtjük), akkor a közegben a gravitáció hatására áramlások alakulnak ki: a meleg (kisebb sűrűségű) anyag felfelé, a hideg (nagyobb sűrűségű) lefelé mozdul el. A hőáramlás csökkenti a közeg alja és teteje közti hőmérséklet-különbséget, de ha a közeg alját folyamatosan melegítjük (vagy a tetejét hűtjük), akkor folyamatos áramlás alakulhat ki. A gravitációs áramlásra rengeteg példát láthatunk a természetben és a hétköznapi gyakorlatban is.

A napsugárzás elsősorban a talajban és a vízfelületeken nyelődik el, azt melegíti fel. A talajtól és a víztől felmelegedő (nedves) levegő felszáll, és eközben kitágul, adiabatikusan lehűl (és a benne lévő vízgőz kicsapódik) – ez a globális légmozgások alapvető hajtóereje.

A fűtőtesttől felmelegedő levegő felszáll, a szobában áramlás alakul ki. Ez szállítja a fűtőtest melegét a szoba többi részébe. Eközben a levegő lehűl, és a szoba másik oldalán leszáll – így záródik az áramlás. Ehhez hasonlóan a kémények huzatát szintén a gravitációs áramlás biztosítja: a kinti levegőnél melegebb füst felfelé száll.

Központi fűtés is építhető gravitációs áramlással: a kazánban felmelegedő víz az egyik csövön a pincéből felfelé, a fűtőtestekben kihűlő víz a másik csövön lefelé áramlik. A tűzhelyre tett lábasban is a folyadékban kialakuló gravitációs áramlás szállítja a hőt a lábas aljáról a felsőbb rétegekbe. (Viszkózusabb folyadékokban nem alakul ki elég erős áramlás, így az étel a lábas alján túlzottan felforrósodik, és az étel odaég. Ilyenkor az ételt keverni kell.)

Télen a tavak és tengerek felülete kezd el hűlni, a hideg víz lesüllyed, ezzel gyorsítva az egész víztömeg kihűlését. A folyamat azonban csak 4 °C-ig tart: az ennél hidegebb víz már kisebb sűrűségű, mint a 4 °C-os, így az a felszínen marad. Emiatt először a felszínen fagy meg a víz. A jégréteg viszont már rosszabb hővezető, lassítja az alatta lévő víz hűlését és megfagyását, így az aránylag sekély vizek se fagynak be fenékig. Ennek rendkívüli jelentőssége volt a sekély vizekben kialakuló földi élet szempontjából (és ma is ez teszi lehetővé a vízi élőlények áttelelését).

Ha egy vékony, viszkózus folyadékréteget egyenletesen melegítünk alulról, akkor a szimmetria miatt sokáig nem alakul ki áramlás (a folyadék „nem tudja eldönteni”, hogy hol kezdjen el felfelé, és hol lefelé áramlani). Amikor a sűrűségkülönbség már nagy lesz, akkor az instabil egyensúly valahol felborul: a meleg anyag bizonyos helyeken felfelé, körülötte a hideg pedig lefelé fog áramlani. Ilyen áramlási mintázatokat meg lehet figyelni egy vékony, alulról melegített olajrétegben is, de a Nap felületén is (ahol az égitest belsejében zajló fúzió által felforrósodott anyag áramlik a hidegebb felszín felé).

Kényszerített áramlások

Súlytalanság állapotában (például műholdakon), vagy ha a közeg fent melegebb, mint lent, gravitációs áramlás egyáltalán nem alakul ki. Más esetekben – például ha az áramlás kialakulásához rendelkezésre álló tér szűk, vagy a csövek vékonyak – a kialakuló áramlás nem elég intenzív a kellő intenzitású hőátadáshoz. Ilyenkor kényszerített áramlásra van szükség, az áramlást ventillátorral, keringtetőszivattyúval lehet kialakítani vagy fokozni.

A számítógépekben (gyakran kellemetlenül zajos) ventillátorok biztosítják a kellő hőcserét. A mai központi fűtések pedig keringtető szivattyúval készülnek (így vékonyabb csövek kellenek – viszont a gázfűtés áramszünetkor is leáll). Legtöbb autóban mind a kettőt alkalmazzák: a motorban felszabaduló hőt a vízpumpával hajtott hűtővíz szállítja a hűtőbe, ahonnan – szükség esetén ventillátorral hajtott – levegő szállítja tovább.

A hőátadás fokozása halmazállapot-változással

A testek felületén a hő átadódik a szilárd test és a környező gáz vagy folyadék között. A hőátadás mértéke értelemszerűen függ a felület nagyságától, de ezen kívül sok más paramétertől is. A közeg áramlása például jelentősen növeli a hőátadás intenzitását. Így nem mindegy a felület iránya sem, hiszen függőleges felület mellett könnyebben alakul ki gravitációs áramlás.

A hőátadás intenzitását nagymértékben fokozza a felületen végbemenő halmazállapot-változás: a párolgó folyadék jelentős hőmennyiséget von el környezetétől. Nagy melegben, fizikai munka és sport közben ezért izzadunk: a szervezet így tud megszabadulni a felesleges hőmennyiségtől. (Ugyanakkor szélben, vizesen veszélyesen ki lehet hűlni.)

A hősugárzás

Nem csak izzó testeknél!

A hősugárzás az izzó testek estében (pl. napsütés, hősugárzó) nem csak a bőrünkkel érzékelhető, hanem látható is (hiszen ilyenkor az elektromágneses sugárzás egy része a látható fény tartományába esik). De nem csak a forró testek, hanem minden test sugároz! A sugárzás intenzitása azonban az abszolút hőmérséklet negyedik hatványával arányos, így a hidegebb testek sugárzása sokkal gyengébb. Ennek ellenére a hővezetés és a hőáramlás mellett a hősugárzásnak is fontos szerepe van a szobahőmérsékletű tárgyak közti hőcserében is. A környezetünkben minden test sugároz, és ugyanakkor el is nyel hősugárzást. Ezen a hőmérsékleten a hősugárzás az elektromágneses spektrum emberi szemmel nem látható, infravörös tartományába esik (erre a célra készített kamerákkal azonban érzékelhető).

Az abszorpciós tényező, feketetest-sugárzás

A testek a rájuk eső hősugárzás egy részét elnyelik, a többit visszaverik (vagy átengedik). A beérkező sugárzás hullámhosszától is függő abszorpciós tényező megadja, hogy a test a ráeső hőáram mekkora részét nyeli el. A tökéletesen tükröző (vagy tökéletesen átlátszó) test abszorpciós tényezője =0, a minden sugárzást elnyelő, „fekete” test abszorpciós tényezője pedig =1. A „fekete” szó azért van idézőjelben, mert itt nem csak látható sugárzásról van szó: az infravörös tartományban egy látható tartományban „színes” test is lehet „fekete”.

A feketetest egy olyan (elvi szempontból is fontos) test, amely minden frekvencián minden hősugárzást elnyel, abszorpciós együtthatója hullámhossztól függetlenül =1. (Valódi anyagok csak jó közelítéssel lehetnek ilyenek.)

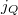A feketetest sugárzásnak intenzitása (a hőáramsűrűség) csak a test abszolút hőmérsékletétől függ (Stefan-Boltzmann-törvény): ahol

a Stefan-Boltzmann-állandó.

Abszorpció és emisszió: miért fekete a hűtőborda?

Egy (nem fekete) test által kisugárzott hőáram

ahol a test sugárzó felülete, pedig az emissziós állandó. Ez az állandó adja meg, hogy az adott test mennyi hőt sugároz ki az ugyanekkora felületű és hőmérsékletű feketetesthez képest. (A feketetest emissziós állandója =1.)

Az emissziós állandó (ami az abszorpciós állandóhoz hasonlóan hullámhosszfüggő) nem független az abszorpciós állandótól. Megmutatjuk, hogy minden testre

azaz ugyanolyan körülmények között a „fekete” testek sugároznak a legerősebben, és a tükröző (vagy átlátszó) testek a leggyengébben. Emiatt festik a hűtőbordákat matt feketére: így tud leadni adott hőmérsékleten, adott felületen a lehető legtöbb hőt.

Az állítás bizonyításához megmutatjuk, hogy ha nem lenne igaz, az ellentmondana a II. főtételnek.

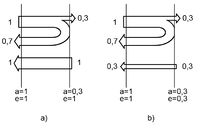
Legyen két párhuzamos felület minden mástól elszigetelve, és legyenek kezdetben azonos hőmérsékletűek. Egymás közt is csak hősugárzással cserélhetnek energiát. Legyen az egyik (a bal oldali) fekete (=1), a másik aránylag jól tükröző (pl. =0,3), ugyanakkor tegyük fel, hogy az állításunkkal ellentétben mindkettőnek mégis =1 az emissziós tényezője. Az 1/a ábra alapján látható, hogy ekkor mindkét oldal ugyanakkora teljesítménnyel sugározna, viszont nem ugyanannyit nyelne el. (A részben tükröző test a beeső sugárzás nagyobb részét visszaveri, amit szintén a fekete test nyel el.) Ilyen módon a két kezdetben egyforma hőmérsékletű test közül az egyik külső hatás nélkül felmelegedne, a másik pedig lehűlne, ami ellentmondana a II. főtételnek. Az 1/b ábrán látható, hogy ha a részben tükröző test emissziós tényezője megegyezik az abszorpciós tényezőjével, akkor mind a két test összesen ugyanannyi energiát nyel el, mint amennyit kisugároz, és így a hőmérsékletek nem változnak.

A hősugárzás spektrális eloszlása

Hőmérsékletmérés színkép alapján

A hősugárzás nem egy hullámhosszon, hanem a teljes elektromágneses spektrumon történik. A spektrális eloszlás azt adja meg, hogy a teljes kisugárzott energia hogyan oszlik el a különböző hullámhosszúságok között. A feketetest-sugárzás spektrális eloszlásának elméleti magyarázata a XIX. század végén még hiányzott. Max Planck 1900 karácsonyán csak az energiakvantum fogalmának bevezetésével tudta megmagyarázni a sugárzási törvényt, ezzel elindítva a XX. századi fizika alapvető elméletét, a kvantummechanikát.

A spektrum függ a sugárzó test hőmérsékletétől. Mint láttuk, a teljes kisugárzott energia arányos az abszolút hőmérséklet negyedik hatványával. Emellett a hőmérséklet növelésével a spektrum a magasabb frekvenciák (kisebb hullámhosszok) felé tolódik. A Wien-féle eltolódási törvény szerint a maximális intenzitáshoz tartozó hullámhossz fordítva arányos az abszolút hőmérséklettel.

Szobahőmérsékleten a sugárzás gyakorlatilag teljesen a nem látható, infravörös tartományba esik. 550-600 °C hőmérséklet felett a test már sugároz annyit a látható tartományban is, hogy a szemünk érzékelje (vörös izzás). A Nap kb. 6000 K hőmérsékletű felületéről érkező napfényben a maximális intenzitás már a látható tartományba esik (a hullámhossza kb. 550 nm, zöld szín).

A sugárzás intenzitása és spektrális eloszlása alapján következtetni lehet a sugárzó test hőmérsékletére. (Természetesen figyelembe kell venni, hogy a valódi testek nem feketetestek.) A pirométer egy ilyen elven működő érintésmentes hőmérő, amivel nagyon nagy hőmérsékletek is mérhetők. A termográfia a fényképezéshez vagy a filmezéshez hasonló képalkotás az infravörös tartományban. A mesterségesen színezett képeken a színek a sugárzó test hőmérsékletét mutatják.

Hősugárzás a természetben, hová verjük a sátrunkat?

Környezetünkben minden test sugároz, természetesen a saját testünk is. A hősugárzásról azonban elsősorban forró testek jutnak eszünkbe, például a napfény, vagy egy vörösen izzó hősugárzó. A szobahőmérsékletű testek sugárzását alig vesszük észre. Ugyanakkor, ha egy hideg betonfal, vagy jégtömb közelében áll valaki, akkor azt érzi, hogy a hideg testből „sugárzik a hideg”. Van „hideg sugárzás” is? Természetesen nincs. A testünkkel közel azonos hőmérsékletű testek sugárzását azért nem érezzük, mert ilyenkor a mi általunk kisugárzott energia és a test által felénk sugárzott energia éppen kiegyenlíti egymást. Ha a környező testek jóval hidegebbek a testünknél, akkor kevesebb sugárzó hő éri irányukból a bőrünket, mint amennyit kisugároz, így lehűl. Ezt érezzük úgy, hogy „sugárzik a hideg”.

Ahhoz, hogy a testhőmérsékletünk állandó maradjon, a testünkben termelődő hőtől (nyugalmi állapotban kb. 50 W) folyamatosan meg kell szabadulnunk. Ezért a testhőmérsékletünknél kicsit hidegebb (20-25 °C-os) környezetben érezzük magunkat kellemesen. Ha a környezet ennél melegebb, akkor csak izzadás (halmazállapot-változás) segítségével tudjuk leadni a felesleges hőt. Ha a környezet sokkal hidegebb, akkor fel kell öltöznünk: a hőszigetelő ruha felülete alacsonyabb hőmérsékletű a testünknél (hiszen ez a hőmérséklet-gradiens kell a hővezetéshez), így kevesebb hőt sugároz ki.

A természetben a testünket a napsugárzás és a környező tárgyak sugárzása éri. A Napból érkező (elsősorban látható fényből és közeli infravörösből álló) sugárzás azonban térben és időben egyenetlenül éri a Földet. Nappal, tiszta időben kb. 1000 W/m teljesítmény ér a Föld felszínén egy napsugárzásra merőleges felületet. Ugyanakkor éjszaka csak a talaj, a környező tárgyak és a légkör sugároz felénk. A tiszta légkör azonban keveset nyel el (kicsi az abszorpciós együtthatója), és így keveset is sugároz (kicsi az emissziós együtthatója). Derült időben az égbolt így csak annyi energiát sugároz, mint egy nagyon hideg test. Ez okozza derült időben az eget „látó” felületek jelentős lehűlését. A környező levegőnél hidegebb tárgyakra pedig harmat vagy dér formájában kicsapódhat a levegő nedvességtartalma.

Hová verjük a sátrunkat, ha éjjel nem akarunk fázni, és reggel szárazon szeretnénk elcsomagolni? Borult időben majdnem mindegy: ilyenkor a felhők visszaverik a Föld felszínéről kisugárzott sugárzást, és így az égbolt erősebben sugároz, nem lesz olyan erős kisugárzás, és az éjszaka melegebb lesz. Derült időben viszont fák alatt érdemes sátrazni: a fák lombja a környező levegővel azonos hőmérsékletű, így sokkal erősebben sugároz, mint a közel átlátszó derült égbolt. Derült nyári éjszakákon az erdőben szárazon és melegen lehet ébredni, míg a réteket vastag harmat borítja.

Üvegházhatás

Az abszorpciós tényezőhöz hasonlóan a testek átlátszósága is hullámhosszfüggő. A sima üveg felület például átlátszó a látható tartományban, de az infravörös sugárzást visszaveri. Ezt a jelenséget használják ki a kertészek az üvegházak építésével: az üveglapok átengedik a napfényt, ami elnyelődik a talajban és a növényekben. A szobahőmérsékletű tárgyak hősugárzását viszont az üveg visszaveri, így az üvegház felmelegszik.

A globális üvegházhatás ugyanilyen elven alapul: a széndioxid, a metán (és kis mértékben a vízgőz is) a látható fényben átlátszók, míg az infra tartományban elnyelik és részben visszaverik a sugárzást. A Földnek, ahhoz hogy ne változzon a hőmérséklete, folyamatosan ki kell sugároznia azt az energiát, amit a Naptól kap (és ami a Föld belsejében radioaktív bomlásokból keletkezik). Ha a légkör kevésbé átlátszó az infravörös tartományban, akkor a felszíni hőmérsékletnek magasabbnak kell lennie ugyanolyan erős kisugárzáshoz.

Az üvegházhatás jelentős része természetes eredetű. A legnagyobb részéért a kis mértékben üvegházhatású, de nagyon nagy mennyiségben jelenlévő vízgőz felelős. Ezen kívül természetes úton kerül széndioxid és metán is a légkörbe. Üvegházhatás nélkül a Földön túl hideg lenne.

A Föld két különböző visszacsatolási mechanizmussal is képes szabályozni a légköri széndioxid mennyiségét:

A (nagyon lassú) geológiai szabályozás lényege, hogy ha nagyon sok a széndioxid a légkörben, akkor felmelegedés következik be. A meleg tengervízben feloldódó széndioxid reagál a szilikátokkal, és karbonátos kőzetekben megköti a felesleges széndioxidot. Ha túl kevés a széndioxid a légkörben, akkor megindul az eljegesedés, a jégtakarók súlya a magmába nyomja a karbonátos kőzeteket, ahol a széndioxid vulkáni tevékenységgel újra a légkörbe jut.

A (kicsit gyorsabb) biológiai szabályozás a növények széndioxid megkötésén alapul. A magas széndioxid-koncentráció okozta meleg éghajlaton intenzívebb a növényi élet, és a széndioxid az élő növényekben és a növényi maradványokban (szén, kőolaj, földgáz) megkötődik. A légköri széndioxid-koncentráció csökkenése lehűlést és a növényzet visszaszorulását eredményezi, így a megkötött széndioxid részben visszajut a légkörbe.

A fosszilis energiahordozók elégetése és a növényzet irtása azonban a légköri széndioxid-koncentráció földtörténeti léptékben nagyon gyors növekedését okozza, ami a természetes változásokhoz képest túl gyors felmelegedést okozhat. Sokak szerint ez ma a legsúlyosabb környezeti veszély.

Hűtés-fűtés

Egy lakás hőháztartása

Az energiaárak növekedésével egyre inkább előtérbe kerül a lakóházak hőszigetelése. Érdemes áttekinteni egy lakás teljes hőháztartását!

A lakásba bejutó energia meghatározásakor a fűtésen kívül figyelembe kell venni az ablakokon keresztül bejutó napfényt (ami megfelelő tájolás esetében télen se elhanyagolható – nyáron viszont árnyékolással csökkenthető), a lakásban működő háztartási eszközök hőleadását (a berendezések – hűtőgép, hajszárító, számítógép, tévé, belső világítás stb. – elektromos fogyasztása végül hővé alakul), és a lakásban élő emberek hőtermelését is. Ezen kívül nyáron (amikor kint melegebb van, mint a lakásban) hővezetéssel a falakon és nyílászárókon át is befelé áramlik az energia.

A lakás belsejéből télen (amikor a kint hidegebb van, mint a lakásban) a falakon és a nyílászárókon keresztül hővezetéssel jut ki az energia. Ezen belül hagyományos épületeknél meghatározó a nyílászárók és a rossz tervezés vagy kivitelezés miatt kialakuló hőhidak (például a hőszigetelésen átvezető vasbeton szerkezetek) szerepe. Jelentős energiaveszteséget okoz a rosszul záródó ablakoknál kialakuló folyamatos légáramlás, a kéményeken keresztül távozó meleg füst és levegő, valamint a szellőzés is. Nyári hőségben klímaberendezéssel lehet mesterségesen elvonni hőt a lakásból.

A kinti hőmérsékletnek – különösen nyáron – jelentős napi ingadozása van. Ezért fontos a ház hőkapacitása is: a vastag, nagy tömegű falakban tárolt energia csökkenti a lakásban a napi hőmérsékletingadozást.

Az épület alakja és tájolása is jelentősen befolyásolja a hőháztartást. Ugyanahhoz az alapterülethez egy kompakt, nagyjából kocka alakú épület esetében tartozik a legkisebb hőleadó felület. Ugyanakkor a téli besugárzás jobb kihasználásához ettől eltérő (kb. 1:1,6) oldalarányú épület az optimális, természetesen megfelelő tájolással.

A szinte semmi külső energiát nem igénylő épületek világszerte használt német szabványa a passzívház. Az ilyen épületek évente legfeljebb 15 kW/m energiát használnak fűtésre-hűtésre. Az ilyen épületekben a vastag (50 cm), jó hőszigetelésű falakkal, a hézagmentes, háromrétegű, nemesgáztöltésű nyílászárókkal, valamint hőhídmentes konstrukcióval minimálisra csökkentik a hőveszteséget. A szellőzést a talajban kígyózó csővezetéken keresztül beáramló levegővel biztosítják: a talajban hosszan kanyargó csőben télen melegszik, nyáron lehűl a levegő. Ezután télen a házból kilépő levegő melegíti tovább egy hőcserélőben. A minimális veszteséget a megfelelő tájolásnak köszönhető besugárzás, és a házban lakó emberek, valamint a háztartási eszközök hőkibocsátása biztosítja. A használati meleg vizet napkollektorok melegítik, a nyári hűtést a talajban előhűtött levegő és megfelelő árnyékolás biztosítja. Gázbekötés, kémény nincsen. Az első magyar passzívház Szadán épült.

Az elektromos energia részben vagy egészében napelemekkel, vagy egyéb megújuló energiaforrásokkal is előállítható. Léteznek már pozitív energiamérlegű aktív házak, melyek egy év alatt több energiát termelnek (és juttatnak vissza az elektromos hálózatba), mint amennyit felhasználnak.

---

Vissza a Fizika 1i nyitóoldalára

1. Tér és idő

2. Mozgás és megjelenítése

3. Megmaradási törvények a mechanikában

4. Rezgések

5. Rend és rendetlenség

6. Hideg-meleg