„Folyadékkristályok vizsgálata” változatai közötti eltérés

A Fizipedia wikiből
 
(4 szerkesztő 29 közbeeső változata nincs mutatva)
17. sor: 17. sor:
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
 
[[Kategória:Szerkesztő:Vankó]]
 
[[Kategória:Szerkesztő:Vankó]]
−
 
−
Szerkesztés alatt!
 
  
 
''A mérés célja''
 
''A mérés célja''
31. sor: 29. sor:
  
 
* kiértékeljük a mérési eredményeket.
 
* kiértékeljük a mérési eredményeket.
 +
  
 
__TOC__
 
__TOC__
38. sor: 37. sor:
 
===Folyadékkristály===
 
===Folyadékkristály===
  
−
A folyadékkristály (LC = Liquid Crystal) olyan állapota az anyagnak, ami a kristályos szilárd állapot és az amorf folyadék állapot között van. A nematikus LC-k szerves vegyületek, melyek hosszúkás, tűszerű molekulákból állnak. A molekulák orientációja (irányítottsága) könnyen egy irányba rendezhető és szabályozható elektromos erőtér segítségével. Az LC eszközökhöz azonos vagy jól meghatározott orientációjú LC molekulákra van szükség. A méréshez használt LC cella felépítése az ''1. ábrán'' látható. Az üveg hordozólemezeket először egy vékony, elektromosan vezető, de optikailag átlátszó indium-ón-oxid (ITO = Indium-Tin-Oxide) réteggel vonják be, majd egy vékony polyimid (PI) rendező réteget alakítanak ki. Ezután a PI réteg felszínét megcsiszolják, és ezzel mikroszkopikus árkokat alakítanak ki rajta. Ezek az árkok rendezik egy irányba az LC molekulákat, melyeket szendvicsszerűen két hordozó közé helyeznek. Ezzel a csiszolásos módszerrel a kívánt irányba orientált, jól rendezett LC-molekulák kerülnek a hordozók felszínére, és a molekulák közt ható erők hatására az egész LC-hasáb azonos orientációjú lesz. Egy adott helyen a molekula-orientációt az LC adott helyen lévő direktorának nevezik.
+
{{fig2|Foly_kep_1.JPG|fig:1|1. ábra}}
  
−
Az LC cellában megfigyelhető az ún. kettőstörés jelensége, amikor az anyagnak kétféle fő törésmutatója van. Ha a fény a direktor irányában terjed, akkor az összes polarizációs összetevő ugyanakkora $\v_o=\frac{c}{n_o}$ sebességgel terjed, ahol $n_o$ az ordinárius (rendes) törésmutató. Ezt a terjedési irányt (a direktor irányát) nevezik a cella optikai tengelyének. Ha a fény az optikai tengelyre merőleges irányba terjed, akkor két terjedési sebesség van. A fény elektromos mezejének az optikai tengelyre merőlegesen polarizált része ekkor is $v_o$ sebességgel halad, az optikai tengellyel párhuzamosan polarizált rész sebessége viszont $v_e=\frac{c}{n_e}$, ahol $n_e$ az extraordinárius (különleges) törésmutató. Az optikai anizotrópia (pontosabban annak mértéke) az extraordinárius és az ordinárius törésmutató különbsége: $\Delta n= n_e – n_o$.
+
 
 +
{{figN|LC_cella.png|fig:2|2. ábra|500}}
 +
 
 +
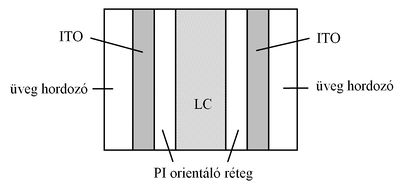
A folyadékkristály (LC = Liquid Crystal) olyan állapota az anyagnak, ami a kristályos szilárd állapot és az amorf folyadék állapot között van. A nematikus LC-k szerves vegyületek, melyek hosszúkás, tűszerű molekulákból állnak. A molekulák orientációja (irányítottsága) könnyen egy irányba rendezhető és szabályozható elektromos erőtér segítségével. Az LC eszközökhöz azonos vagy jól meghatározott orientációjú LC molekulákra van szükség. A méréshez használt LC cella felépítése az [[#fig:1|1. ábrán]] látható. Az üveg hordozólemezeket először egy vékony, elektromosan vezető, de optikailag átlátszó indium-ón-oxid (ITO = Indium-Tin-Oxide) réteggel vonják be, majd egy vékony polyimid (PI) rendező réteget alakítanak ki. Ezután a PI réteg felszínét megcsiszolják, és ezzel mikroszkopikus árkokat alakítanak ki rajta. Ezek az árkok rendezik egy irányba az LC molekulákat, melyeket szendvicsszerűen két hordozó közé helyeznek. Ezzel a csiszolásos módszerrel a kívánt irányba orientált, jól rendezett LC-molekulák kerülnek a hordozók felszínére, és a molekulák közt ható erők hatására az egész LC-hasáb azonos orientációjú lesz. Egy adott helyen a molekula-orientációt az LC adott helyen lévő direktorának nevezik.
 +
 
 +
Az LC cellában megfigyelhető az ún. kettőstörés jelensége, amikor az anyagnak kétféle fő törésmutatója van. Ha a fény a direktor irányában terjed, akkor az összes polarizációs összetevő ugyanakkora $v_o=\frac{c}{n_o}$ sebességgel terjed, ahol $n_o$ az ordinárius (rendes) törésmutató. Ezt a terjedési irányt (a direktor irányát) nevezik a cella optikai tengelyének. Ha a fény az optikai tengelyre merőleges irányba terjed, akkor két terjedési sebesség van. A fény elektromos mezejének az optikai tengelyre merőlegesen polarizált része ekkor is $v_o$ sebességgel halad, az optikai tengellyel párhuzamosan polarizált rész sebessége viszont $v_e=\frac{c}{n_e}$, ahol $n_e$ az extraordinárius (különleges) törésmutató. Az optikai anizotrópia (pontosabban annak mértéke) az extraordinárius és az ordinárius törésmutató különbsége: $\Delta n= n_e – n_o$.
  
 
Az LC cella optikai viselkedése a cella elé helyezett polarizátor és a cella mögé helyezett analizátor polárszűrők segítségével vizsgálható.
 
Az LC cella optikai viselkedése a cella elé helyezett polarizátor és a cella mögé helyezett analizátor polárszűrők segítségével vizsgálható.
46. sor: 50. sor:
 
====90°-kal elcsavart nematikus LC cella====
 
====90°-kal elcsavart nematikus LC cella====
  
−
A $90^\circ$-kal elcsavart nematikus cellában (''2. ábra'') (TN = Twisted Nematic) a hátsó felület LC direktora $90^\circ$-kal el van forgatva az első felülethez képest. Elől a helyi direktor párhuzamos a polarizátor (első polárszűrő) polarizációs irányával. A belépő polarizálatlan fény az első polárszűrőben lineárisan polarizált fénnyé változik.
+
{{fig|Foly_kep_2.JPG|fig:3|3. ábra}}
  
−
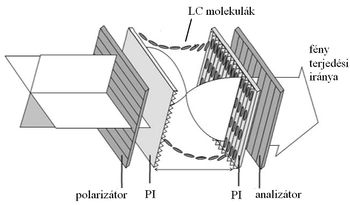
Ha egy lineárisan polarizált fény halad át egy $90^\circ$ TN cellán, akkor polarizációs iránya követi az LC direktorának csavarodását (a polarizált fény csak $n_e$-t érzékeli), így a kilépő fénysugár is lineárisan polarizált marad, csak polarizációs iránya $90^\circ$-kal elfordul. (Ezt $n_e$ által okozott polarizációs forgató hatásnak nevezzük, ehhez hasonlóan van $n_o$ által okozott forgató hatás is.) Eszerint a $90^\circ$ TN cella normál fekete (NB = Normal Black) üzemmódjához az analizátor (a második polárszűrő) polarizációs irányát párhuzamosra kell állítani a polarizátor (az első polárszűrő) polarizációs irányával.
+
A 90°-kal elcsavart nematikus cellában ([[#fig:3|3. ábra]]) (TN = Twisted Nematic) a hátsó felület LC direktora 90°-kal el van forgatva az első felülethez képest. Elől a helyi direktor párhuzamos a polarizátor (első polárszűrő) polarizációs irányával. A belépő polarizálatlan fény az első polárszűrőben lineárisan polarizált fénnyé változik.
 +
 
 +
Ha egy lineárisan polarizált fény halad át egy 90° TN cellán, akkor polarizációs iránya követi az LC direktorának csavarodását (a polarizált fény csak $n_e$-t érzékeli), így a kilépő fénysugár is lineárisan polarizált marad, csak polarizációs iránya 90°-kal elfordul. (Ezt $n_e$ által okozott polarizációs forgató hatásnak nevezzük, ehhez hasonlóan van $n_o$ által okozott forgató hatás is.) Eszerint a 90° TN cella normál fekete (NB = Normal Black) üzemmódjához az analizátor (a második polárszűrő) polarizációs irányát párhuzamosra kell állítani a polarizátor (az első polárszűrő) polarizációs irányával.
  
 
Azonban ha az LC cellára kapcsolt $U$ feszültség értéke elér egy kritikus $U_c$ értéket, az LC molekulák igyekeznek beállni az alkalmazott külső elektromos tér irányába, ami itt megegyezik a fény terjedési irányával. Ennél fogva az LC cella polarizációs irányt elforgató hatása folyamatosan csökken, és a fény átjuthat az analizátoron (a második polárszűrőn). A cella elektro-optikai kapcsolási meredekségét a $\gamma = (U_{90}–U_{10})/U_{10}$ képlet definiálja, ahol $U_{10}$ és $U_{90}$ azok a feszültségek, ahol a cellán áthaladó fény intenzitása eléri a maximális fényintenzitás 10 %-át illetve 90 %-át.
 
Azonban ha az LC cellára kapcsolt $U$ feszültség értéke elér egy kritikus $U_c$ értéket, az LC molekulák igyekeznek beállni az alkalmazott külső elektromos tér irányába, ami itt megegyezik a fény terjedési irányával. Ennél fogva az LC cella polarizációs irányt elforgató hatása folyamatosan csökken, és a fény átjuthat az analizátoron (a második polárszűrőn). A cella elektro-optikai kapcsolási meredekségét a $\gamma = (U_{90}–U_{10})/U_{10}$ képlet definiálja, ahol $U_{10}$ és $U_{90}$ azok a feszültségek, ahol a cellán áthaladó fény intenzitása eléri a maximális fényintenzitás 10 %-át illetve 90 %-át.
56. sor: 62. sor:
 
====Homogén, párhuzamosan rendezett LC cella====
 
====Homogén, párhuzamosan rendezett LC cella====
  
−
A párhuzamosan rendezett LC cella esetében az elülső és a hátsó hordozón lévő direktorok párhuzamosak egymással. Ha egy polarizált fénysugár úgy esik a párhuzamosan rendezett cellára, hogy polarizációs iránya pár-huzamos az LC cella direktorával (a csiszolt vájatok irá-nyával), akkor semmi lényeges változás nem történik, mivel a fény tisztán extraordinárius sugárként viselkedik.  
+
A párhuzamosan rendezett LC cella esetében az elülső és a hátsó hordozón lévő direktorok párhuzamosak egymással. Ha egy polarizált fénysugár úgy esik a párhuzamosan rendezett cellára, hogy polarizációs iránya párhuzamos az LC cella direktorával (a csiszolt vájatok irányával), akkor semmi lényeges változás nem történik, mivel a fény tisztán extraordinárius sugárként viselkedik.  
−
Másrészt, ha egy lineárisan polarizált fénysugár merő-legesen esik a párhuzamosan rendezett cellára, de polari-zációs iránya = 45 szöget zár be a cella direktorának irányával (3. ábra), akkor fáziskülönbség (δ) lép fel az extraordinárius és az ordinárius sugarak különböző terje-dési sebessége miatt. Ebben a = 45-os elrendezésben, ha a két polárszűrő egymással párhuzamos ill. merőleges, akkor a rendszer fényáteresztő képességét a következő összefüggések írják le:
+
 
 +
{{fig|Foly_kep_3.JPG|fig:4|4. ábra}}
 +
 
 +
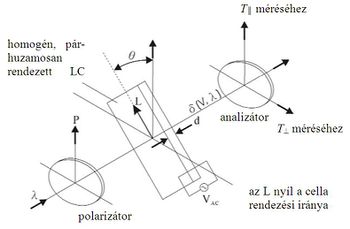
Másrészt, ha egy lineárisan polarizált fénysugár merőlegesen esik a párhuzamosan rendezett cellára, de polarizációs iránya $\theta=$ 45° szöget zár be a cella direktorának irányával ([[#fig:4|4. ábra]]), akkor fáziskülönbség ($\delta$) lép fel az extraordinárius és az ordinárius sugarak különböző terjedési sebessége miatt. Ebben a $\theta=$ 45°-os elrendezésben, ha a két polárszűrő egymással párhuzamos ill. merőleges, akkor a rendszer fényáteresztő képességét a következő összefüggések írják le:
 +
 
 +
$$ T_\parallel = 1-\sin^2 2\theta \sin^2 \frac{\delta}{2} = \cos^2 \frac{\delta}{2}, $$
 +
 
 +
$$ T_\perp= \sin^2 2\theta \sin^2 \frac{\delta}{2} = \sin^2 \frac{\delta}{2}, $$
 +
 
 +
ahol $\parallel$ és $\perp$ az analizátor és a polarizátor polarizációs irányának párhuzamos ill. merőleges állására utal.
 +
 
 +
A $\delta$ fáziskülönbség kifejezhető:
 +
 
 +
$$ \delta = \frac{2\pi d \Delta n(U,\lambda)}{\lambda}, $$
 +
 
 +
ahol $d$ az LC réteg vastagsága, $\lambda$ a fény hullámhossza levegőben, $U$ a váltakozó feszültség effektív értéke, és $\Delta n$ (ami $\lambda$ és $U$ függvénye) az LC cella optikai anizotrópiájának mértéke. Azt is meg kell jegyezni, hogy ha $U = 0$, akkor $\Delta n$ maximális, és így $\delta$-nak is ekkor van maximuma. Tehát $\Delta n$ csökken, ha $U$ növekszik.
 +
 
 +
===A méréshez használt egyéb optikai eszközök===
 +
 
 +
====Lézerdióda====
 +
 
 +
A méréshez használt fényforrás egy 650 nm hullámhosszúságú félvezető lézer. Ha a lézerdióda (LD) árama nagyobb egy küszöbáramnál (threshold current), a dióda monokromatikus, részlegesen polarizált, koherens fényt bocsát ki. Ha a lézerdióda árama kisebb a küszöbértéknél, a kibocsátott fény intenzitása nagyon kicsi. A küszöbáram felett a fényerősség az áramerősség növekedésével rohamosan nő, és a két mennyiség között lineáris kapcsolat van, egészen egy $I_m$ áramértékig. Ha az áram tovább nő, a fényerősség növekedési üteme a lézerdióda melegedése miatt (kis mértékben) csökken. A lézerdióda optimális működési tartománya az, ahol a fényerősség lineárisan függ az áramerősségtől. Az $I_{th}$ küszöbáram definíció szerint az áramerősség tengely és a lineáris tartományra illesztett egyenes meghosszabbításának metszéspontja.
 +
A lézerfény csak részlegesen polarizált. A polarizáció mértékét a $\beta= \mathcal{I}_p/ ( \mathcal{I}_p + \mathcal{I}_u)$ aránnyal lehet jellemezni, ahol $\mathcal{I}_p$ és $\mathcal{I}_u$ a lézerfény polarizált és polarizálatlan összetevőjének intenzitása.
 +
 
 +
{{fig|Foly_kep_4.JPG|fig:5|5. ábra}}
 +
 
 +
{{fig|Foly_kep_5.JPG|fig:6|6. ábra}}
 +
 
 +
 
 +
====Fotodetektor====
 +
 
 +
A méréshez használt fotodetektor egy fotodiódából és egy áramerősítőből áll. Ha a fotodiódára tápfeszültség van kapcsolva, akkor a diódára eső fény hatására áram generálódik (fotoáram). Állandó hőmérsékleten, monokromatikus fény estében a fotoáram egyenesen arányos a fényintenzitással. Az áramerősítő ezt a fotoáramot egy kimenő feszültségjellé alakítja. A fotodetektor kétféle erősítéssel működhet: "''high''" és "''low''". Azonban a fotodióda tulajdonságai miatt, ha a fényerősség nagyon nagy, a kimenő feszültség 8 V tájékán telítődik (nem nő tovább), ilyenkor a fotodióda már nem működik helyesen. Emiatt a fotodetektor akkor működik megfelelően, amikor a lineáris tartományban van. Ha a fényerősség olyan nagy, hogy a fotodióda eléri a telítődést, akkor a fotodetektor már nem mutatja helyesen a fényintenzitást.
 +
 
 +
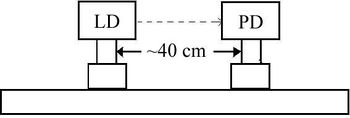
A lézerdióda (LD) és a fotodetektor (PD) elrendezése és elektromos kapcsolása az [[#fig:5|5.]] és a [[#fig:6|6.]] ábrán látható.
 +
 
 +
====Polárszűrők====
 +
 
 +
{{fig|Foly_kep_6.JPG|fig:7|7. ábra}}
 +
 
 +
A forgatható foglalatba szerelt polárszűrők az áthaladó fényt lineárisan polarizálják. Az első polárszűrőt polarizátornak, a másodikat analizátornak szokás nevezni, de felépítésük azonos. A polárszűrő (''P'') optikai elrendezése a [[#fig:7|7. ábrán]] látható.
 +
 
 +
 
 +
 
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{figN|LC_elrend.png|fig:8|8. ábra|500}}
 +
|-
 +
|}
 +
 
 +
==Mérési feladatok==
 +
 
 +
[[A méréshez rendelkezésre álló eszközök: Folyadékkristályok vizsgálata|A méréshez rendelkezésre álló eszközök]]
 +
 
 +
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
 +
 
 +
'''FIGYELEM! Ne nézzen bele közvetlenül a lézersugárba! Tönkreteheti a szemét!'''
 +
 
 +
'''A mérés végén ne felejtse el kikapcsolni a lézert, és kivenni az elemet a fotodetektorból!'''
 +
<!--'''0.''' Polárszűrők és folyadékkristályos kijelző vizuális tanulmányozása-->
 +
===A lézerdióda és a fotodetektor beállítása és vizsgálata===
 +
 
 +
'''1.''' Szerelje fel a lézerdiódát és a fotodetektort egy vízszintes egyenes mentés az optikai sínre, ahogy a [[#fig:5|5. ábrán]] látható!
 +
 
 +
* ''Tegye be a fotodetektorba az elemet, csatlakoztassa a kézi multimétert (DC voltmérő állásban), és kapcsolja be a lézerdiódát!''
 +
 
 +
* ''Állítsa be a lézerdióda és a fotodetektor magasságát úgy, hogy a lézersugár vízszintes legyen.
 +
 
 +
A lézerdiódán lévő csavarok segítségével állítsa be, hogy a lézerfény a detektoron lévő kis lyukba jusson, és a fotodetektor maximális értéket mutasson!''
 +
 
 +
'''2.''' Szereljen fel egy polárszűrőt a lézerdióda és a fotodetektor közé, ahogy az a [[#fig:7|7. ábrán]] látható! Győződjön meg róla, hogy a lézersugár a polárszűrő középső részén halad-e át! Állítsa be a polárszűrőt úgy, hogy a beeső fénysugár merőleges legyen a polárszűrő síkjára!
 +
 
 +
* ''Javaslat: Rakjon be egy lyukas papírt a fényútba, és ezen ellenőrizze, hogy a beeső és a visszavert sugár egybeesik-e!''
 +
 
 +
Forgassa körbe a polárszűrőt, és mérje meg az $\mathcal{I}_{max}$ maximális és az $\mathcal{I}_{min}$ minimális fényintenzitást!
 +
Határozza meg a lézerfényben a lineárisan polarizált fény $\beta$ arányát! $\beta \equiv \mathcal{I}_p/ ( \mathcal{I}_p + \mathcal{I}_u) = (\mathcal{I}_{max}-\mathcal{I}_{min})/(\mathcal{I}_{max}+\mathcal{I}_{min})$.
 +
 
 +
'''3.''' Állítsa be a polárszűrőt úgy, hogy a fényintenzitás maximális legyen! Szerelje fel a másik polárszűrőt is az optikai sínre és állítsa be ezt is a fénysugárra merőlegesen! Állítsa a második polárszűrő polarizációs irányát az elsővel párhuzamosra (forgassa addig, amíg a fényintenzitás maximális nem lesz)!
 +
<!--'''4.''' Szereljen fel egy harmadik polárszűrőt a két polárszűrő közé, és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan! Forgassa körbe 5-10°-os lépésekben az LC cellát! Mérje meg, foglalja táblázatba és ábrázolja az áthaladó fény intenzitását a forgatás $\theta$ szögének függvényében!
 +
 
 +
* ''Miért változik a fényintenzitás?''-->
 +
 
 +
===A 90° TN LC cella vizsgálata===
 +
 
 +
'''4.''' Szerelje fel az NB 90° TN LC cellát (sárga drótok) a két polárszűrő közé, és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan!
 +
* ''Ügyeljen arra, hogy a lézersugár a cella közepén haladjon át, mert csak itt tudjuk a ráadott feszültséggel orientálni a molekulákat!''
 +
 
 +
Forgassa körbe 5-10°-os lépésekben az LC cellát! Mérje meg, foglalja táblázatba és ábrázolja az áthaladó fény intenzitását a forgatás $\theta$ szögének függvényében!
 +
 
 +
* ''Miért változik a fényintenzitás?''
 +
 
 +
'''5.''' Állítsa be úgy az LC cellát, hogy az intenzitás minimális legyen (NB mód)! Kapcsoljon a cellára 100 Hz-es négyszögjelet, és változtassa a jel (effektív) feszültségét 0-tól 7 V-ig!
 +
 
 +
* ''Figyeljen arra, hogy a fontos, érdekes pontoknál megfelelően kis lépésekben változtassa a feszültséget!''
 +
 
 +
Mérje meg, foglalja táblázatba és ábrázolja az NB 90° TN LC cella elektro-optikai kapcsolási görbéjét ($\mathcal{I}$ az $U$ függvényében)!
 +
 
 +
Határozza meg a $\gamma \equiv (U_{90}–U_{10})/U_{10}$ kapcsolási meredekséget és az $U_c$ kritikus feszültséget! $U_c$ meghatározásánál vegye figyelembe, hogy $U > U_c$ feszültségnél az $\mathcal{I}$ fényintenzitás $U$ monoton növekvő függvénye!
 +
 
 +
'''6.''' Párhuzamos polarizátor állás mellett forgassa a NB 90° TN LC cellát olyan pozícióba, melyben maximális az intenzitás. Mérje meg a cellára kapcsolt 100 Hz-es négyszögjel effektív feszültségének függvényében az intenzitás változását a 0-7 V tartományban!
 +
 
 +
* ''Értelmezze a megfigyeléseket!''
 +
 
 +
===A párhuzamosan rendezett LC cella vizsgálata===
 +
 
 +
'''7.''' Cserélje ki az NB 90° TN LC cellát a párhuzamosan rendezett cellával (narancssárga drótok), és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan!
 +
 
 +
* ''A lézersugár ismét a cella közepén haladjon át! Egyelőre ne kapcsoljon feszültséget a cellára ($U = 0$)!''
 +
 
 +
Állítsa be a $\theta=$ 45°-os elrendezést! Ehhez állítsa az analizátort a polarizátorral merőleges állásba (forgassa el 90°-kal), majd forgassa a párhuzamosan rendezett LC cellát addig, amíg az átmenő fény intenzitása el nem éri a maximális értékét ($~T_\perp$)! Ez a helyzet valósítja meg a $\theta=$ 45°-os konfigurációt. Jegyezze fel a $~T_\perp$-sel arányos intenzitásértékét! Ezután mérje meg ugyanebben a $\theta=$ 45°-os állásban az áteresztő képességet abban az esetben is, ha az analizátor és a polarizátor polarizációs iránya párhuzamos ($~T_\parallel$)!
 +
 
 +
Tudjuk, hogy a lézerfény hullámhossza 650 nm, az LC réteg vastagsága $d$ = 7,7 μm és hogy $\Delta n \approx 0,25$. Felhasználva $~T_\perp$ és $~T_\parallel$ az előzőek szerint megmért arányát, számítsa ki a $\delta$ fáziskülönbség és a $\Delta n$ optikai anizotrópia pontos értékét az adott LC cellára, $U = 0$ esetében!
 +
 
 +
'''8.''' Az előzőekhez hasonlóan, továbbra is a $\theta=$ 45°-os konfigurációban mérjen! Kapcsoljon 100 Hz-es négyszögjelet a cellára és változtassa a feszültség (effektív) értékét 0-tól 7 V-ig! Mérje meg, foglalja táblázatba és ábrázolja a párhuzamos cella elektro-optikai kapcsolási görbéjét az analizátor és a polarizátor párhuzamos állásánál ($~T_\parallel$)!
  
 +
* ''A függvény szélsőértékeinek közelében vegye fel sűrűbben a pontokat (különösen a 0,5-4,0 V feszültségtartományban)!''
  
 +
Az elektro-optikai kapcsolási görbéből határozza meg a fázistolás mértékét $U = 0$ feszültségnél!
  
 +
* ''Vesse össze az eredményt a 7. feladatban kapott eredménnyel!''
  
 +
Az elektro-optikai kapcsolási görbéből határozza meg azokat az $U_\pi$ feszültségeket, amelyeknél az LC cellában a fázistolás $\pi$ (180°)$!
  
 +
* ''Ne felejtse el, hogy $\Delta n$ (és így $\delta$ is) az $U$ feszültség csökkenő függvénye!''
  
 +
Az elektro-optikai kapcsolási görbéből határozza meg azt a minimális $U$ feszültséget, ahol a cellából kilépő fény cirkulárisan polarizált!
  
 +
* ''A fény akkor válik cirkulárisan polarizálttá, ha a fázistolás $\pi/2$ páratlan többszöröse.''
  
 +
'''A mérés végén ne felejtse el kikapcsolni a lézert, és kivenni az elemet a fotodetektorból!'''
  
 
</wlatex>
 
</wlatex>

A lap jelenlegi, 2013. november 12., 19:04-kori változata


A mérés célja

  • megismerkedni a folyadékkristályok tulajdonságaival és egyszerű elektrooptikai mérésekkel.

Ennek érdekében

  • röviden bemutatjuk a nematikus folyadékkristály tulajdonságait,
  • optikai és elektrooptikai méréseket végzünk különböző folyadékkristály cellákkal,
  • kiértékeljük a mérési eredményeket.


Tartalomjegyzék


Elméleti összefoglaló

Folyadékkristály

1. ábra


2. ábra

A folyadékkristály (LC = Liquid Crystal) olyan állapota az anyagnak, ami a kristályos szilárd állapot és az amorf folyadék állapot között van. A nematikus LC-k szerves vegyületek, melyek hosszúkás, tűszerű molekulákból állnak. A molekulák orientációja (irányítottsága) könnyen egy irányba rendezhető és szabályozható elektromos erőtér segítségével. Az LC eszközökhöz azonos vagy jól meghatározott orientációjú LC molekulákra van szükség. A méréshez használt LC cella felépítése az 1. ábrán látható. Az üveg hordozólemezeket először egy vékony, elektromosan vezető, de optikailag átlátszó indium-ón-oxid (ITO = Indium-Tin-Oxide) réteggel vonják be, majd egy vékony polyimid (PI) rendező réteget alakítanak ki. Ezután a PI réteg felszínét megcsiszolják, és ezzel mikroszkopikus árkokat alakítanak ki rajta. Ezek az árkok rendezik egy irányba az LC molekulákat, melyeket szendvicsszerűen két hordozó közé helyeznek. Ezzel a csiszolásos módszerrel a kívánt irányba orientált, jól rendezett LC-molekulák kerülnek a hordozók felszínére, és a molekulák közt ható erők hatására az egész LC-hasáb azonos orientációjú lesz. Egy adott helyen a molekula-orientációt az LC adott helyen lévő direktorának nevezik.

Az LC cellában megfigyelhető az ún. kettőstörés jelensége, amikor az anyagnak kétféle fő törésmutatója van. Ha a fény a direktor irányában terjed, akkor az összes polarizációs összetevő ugyanakkora 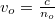\setbox0\hbox{$v_o=\frac{c}{n_o}$}% \message{//depth:\the\dp0//}% \box0% sebességgel terjed, ahol 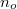\setbox0\hbox{$n_o$}% \message{//depth:\the\dp0//}% \box0% az ordinárius (rendes) törésmutató. Ezt a terjedési irányt (a direktor irányát) nevezik a cella optikai tengelyének. Ha a fény az optikai tengelyre merőleges irányba terjed, akkor két terjedési sebesség van. A fény elektromos mezejének az optikai tengelyre merőlegesen polarizált része ekkor is 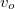\setbox0\hbox{$v_o$}% \message{//depth:\the\dp0//}% \box0% sebességgel halad, az optikai tengellyel párhuzamosan polarizált rész sebessége viszont 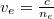\setbox0\hbox{$v_e=\frac{c}{n_e}$}% \message{//depth:\the\dp0//}% \box0%, ahol 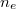\setbox0\hbox{$n_e$}% \message{//depth:\the\dp0//}% \box0% az extraordinárius (különleges) törésmutató. 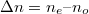Az optikai anizotrópia (pontosabban annak mértéke) az extraordinárius és az ordinárius törésmutató különbsége: \setbox0\hbox{$\Delta n= n_e – n_o$}% \message{//depth:\the\dp0//}% \box0%.

Az LC cella optikai viselkedése a cella elé helyezett polarizátor és a cella mögé helyezett analizátor polárszűrők segítségével vizsgálható.

90°-kal elcsavart nematikus LC cella

3. ábra

A 90°-kal elcsavart nematikus cellában (3. ábra) (TN = Twisted Nematic) a hátsó felület LC direktora 90°-kal el van forgatva az első felülethez képest. Elől a helyi direktor párhuzamos a polarizátor (első polárszűrő) polarizációs irányával. A belépő polarizálatlan fény az első polárszűrőben lineárisan polarizált fénnyé változik.

Ha egy lineárisan polarizált fény halad át egy 90° TN cellán, akkor polarizációs iránya követi az LC direktorának csavarodását (a polarizált fény csak 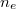\setbox0\hbox{$n_e$}% \message{//depth:\the\dp0//}% \box0%-t érzékeli), így a kilépő fénysugár is lineárisan polarizált marad, csak polarizációs iránya 90°-kal elfordul. (Ezt 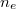\setbox0\hbox{$n_e$}% \message{//depth:\the\dp0//}% \box0% által okozott polarizációs forgató hatásnak nevezzük, ehhez hasonlóan van 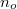\setbox0\hbox{$n_o$}% \message{//depth:\the\dp0//}% \box0% által okozott forgató hatás is.) Eszerint a 90° TN cella normál fekete (NB = Normal Black) üzemmódjához az analizátor (a második polárszűrő) polarizációs irányát párhuzamosra kell állítani a polarizátor (az első polárszűrő) polarizációs irányával.

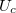Azonban ha az LC cellára kapcsolt \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% feszültség értéke elér egy kritikus \setbox0\hbox{$U_c$}% \message{//depth:\the\dp0//}% \box0% értéket, az LC molekulák igyekeznek beállni az alkalmazott külső elektromos tér irányába, ami itt megegyezik a fény terjedési irányával. Ennél fogva az LC cella polarizációs irányt elforgató hatása folyamatosan csökken, és a fény átjuthat az analizátoron (a második polárszűrőn). 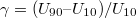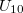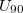A cella elektro-optikai kapcsolási meredekségét a \setbox0\hbox{$\gamma = (U_{90}–U_{10})/U_{10}$}% \message{//depth:\the\dp0//}% \box0% képlet definiálja, ahol \setbox0\hbox{$U_{10}$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$U_{90}$}% \message{//depth:\the\dp0//}% \box0% azok a feszültségek, ahol a cellán áthaladó fény intenzitása eléri a maximális fényintenzitás 10 %-át illetve 90 %-át.

Megjegyzendő, hogy egyenfeszültség alkalmazása esetén elektrolízis indulna be a cellában, mely a cella károsodásához vezetne. Emiatt a cella kapcsolásához váltófeszültséget használunk.

Homogén, párhuzamosan rendezett LC cella

A párhuzamosan rendezett LC cella esetében az elülső és a hátsó hordozón lévő direktorok párhuzamosak egymással. Ha egy polarizált fénysugár úgy esik a párhuzamosan rendezett cellára, hogy polarizációs iránya párhuzamos az LC cella direktorával (a csiszolt vájatok irányával), akkor semmi lényeges változás nem történik, mivel a fény tisztán extraordinárius sugárként viselkedik.

4. ábra

Másrészt, ha egy lineárisan polarizált fénysugár merőlegesen esik a párhuzamosan rendezett cellára, de polarizációs iránya 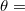\setbox0\hbox{$\theta=$}% \message{//depth:\the\dp0//}% \box0% 45° szöget zár be a cella direktorának irányával (4. ábra), akkor fáziskülönbség (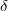\setbox0\hbox{$\delta$}% \message{//depth:\the\dp0//}% \box0%) lép fel az extraordinárius és az ordinárius sugarak különböző terjedési sebessége miatt. Ebben a 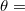\setbox0\hbox{$\theta=$}% \message{//depth:\the\dp0//}% \box0% 45°-os elrendezésben, ha a két polárszűrő egymással párhuzamos ill. merőleges, akkor a rendszer fényáteresztő képességét a következő összefüggések írják le:

\[ T_\parallel = 1-\sin^2 2\theta \sin^2 \frac{\delta}{2} = \cos^2 \frac{\delta}{2}, \]
\[ T_\perp= \sin^2 2\theta \sin^2 \frac{\delta}{2} = \sin^2 \frac{\delta}{2}, \]

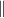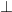ahol \setbox0\hbox{$\parallel$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\perp$}% \message{//depth:\the\dp0//}% \box0% az analizátor és a polarizátor polarizációs irányának párhuzamos ill. merőleges állására utal.

A 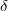\setbox0\hbox{$\delta$}% \message{//depth:\the\dp0//}% \box0% fáziskülönbség kifejezhető:

\[ \delta = \frac{2\pi d \Delta n(U,\lambda)}{\lambda}, \]

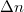ahol \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0% az LC réteg vastagsága, \setbox0\hbox{$\lambda$}% \message{//depth:\the\dp0//}% \box0% a fény hullámhossza levegőben, \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% a váltakozó feszültség effektív értéke, és \setbox0\hbox{$\Delta n$}% \message{//depth:\the\dp0//}% \box0% (ami \setbox0\hbox{$\lambda$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% függvénye) az LC cella optikai anizotrópiájának mértéke. 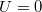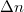Azt is meg kell jegyezni, hogy ha \setbox0\hbox{$U = 0$}% \message{//depth:\the\dp0//}% \box0%, akkor \setbox0\hbox{$\Delta n$}% \message{//depth:\the\dp0//}% \box0% maximális, és így 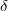\setbox0\hbox{$\delta$}% \message{//depth:\the\dp0//}% \box0%-nak is ekkor van maximuma. Tehát 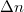\setbox0\hbox{$\Delta n$}% \message{//depth:\the\dp0//}% \box0% csökken, ha \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% növekszik.

A méréshez használt egyéb optikai eszközök

Lézerdióda

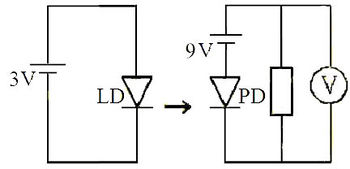
A méréshez használt fényforrás egy 650 nm hullámhosszúságú félvezető lézer. Ha a lézerdióda (LD) árama nagyobb egy küszöbáramnál (threshold current), a dióda monokromatikus, részlegesen polarizált, koherens fényt bocsát ki. Ha a lézerdióda árama kisebb a küszöbértéknél, a kibocsátott fény intenzitása nagyon kicsi. A küszöbáram felett a fényerősség az áramerősség növekedésével rohamosan nő, és a két mennyiség között lineáris kapcsolat van, egészen egy 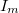\setbox0\hbox{$I_m$}% \message{//depth:\the\dp0//}% \box0% áramértékig. Ha az áram tovább nő, a fényerősség növekedési üteme a lézerdióda melegedése miatt (kis mértékben) csökken. A lézerdióda optimális működési tartománya az, ahol a fényerősség lineárisan függ az áramerősségtől. 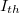Az \setbox0\hbox{$I_{th}$}% \message{//depth:\the\dp0//}% \box0% küszöbáram definíció szerint az áramerősség tengely és a lineáris tartományra illesztett egyenes meghosszabbításának metszéspontja. A lézerfény csak részlegesen polarizált. 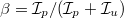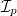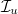A polarizáció mértékét a \setbox0\hbox{$\beta= \mathcal{I}_p/ ( \mathcal{I}_p + \mathcal{I}_u)$}% \message{//depth:\the\dp0//}% \box0% aránnyal lehet jellemezni, ahol \setbox0\hbox{$\mathcal{I}_p$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\mathcal{I}_u$}% \message{//depth:\the\dp0//}% \box0% a lézerfény polarizált és polarizálatlan összetevőjének intenzitása.

5. ábra
6. ábra


Fotodetektor

A méréshez használt fotodetektor egy fotodiódából és egy áramerősítőből áll. Ha a fotodiódára tápfeszültség van kapcsolva, akkor a diódára eső fény hatására áram generálódik (fotoáram). Állandó hőmérsékleten, monokromatikus fény estében a fotoáram egyenesen arányos a fényintenzitással. Az áramerősítő ezt a fotoáramot egy kimenő feszültségjellé alakítja. A fotodetektor kétféle erősítéssel működhet: "high" és "low". Azonban a fotodióda tulajdonságai miatt, ha a fényerősség nagyon nagy, a kimenő feszültség 8 V tájékán telítődik (nem nő tovább), ilyenkor a fotodióda már nem működik helyesen. Emiatt a fotodetektor akkor működik megfelelően, amikor a lineáris tartományban van. Ha a fényerősség olyan nagy, hogy a fotodióda eléri a telítődést, akkor a fotodetektor már nem mutatja helyesen a fényintenzitást.

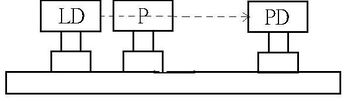
A lézerdióda (LD) és a fotodetektor (PD) elrendezése és elektromos kapcsolása az 5. és a 6. ábrán látható.

Polárszűrők

7. ábra

A forgatható foglalatba szerelt polárszűrők az áthaladó fényt lineárisan polarizálják. Az első polárszűrőt polarizátornak, a másodikat analizátornak szokás nevezni, de felépítésük azonos. A polárszűrő (P) optikai elrendezése a 7. ábrán látható.




8. ábra

Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.

FIGYELEM! Ne nézzen bele közvetlenül a lézersugárba! Tönkreteheti a szemét!

A mérés végén ne felejtse el kikapcsolni a lézert, és kivenni az elemet a fotodetektorból!

A lézerdióda és a fotodetektor beállítása és vizsgálata

1. Szerelje fel a lézerdiódát és a fotodetektort egy vízszintes egyenes mentés az optikai sínre, ahogy a 5. ábrán látható!

  • Tegye be a fotodetektorba az elemet, csatlakoztassa a kézi multimétert (DC voltmérő állásban), és kapcsolja be a lézerdiódát!
  • Állítsa be a lézerdióda és a fotodetektor magasságát úgy, hogy a lézersugár vízszintes legyen.

A lézerdiódán lévő csavarok segítségével állítsa be, hogy a lézerfény a detektoron lévő kis lyukba jusson, és a fotodetektor maximális értéket mutasson!

2. Szereljen fel egy polárszűrőt a lézerdióda és a fotodetektor közé, ahogy az a 7. ábrán látható! Győződjön meg róla, hogy a lézersugár a polárszűrő középső részén halad-e át! Állítsa be a polárszűrőt úgy, hogy a beeső fénysugár merőleges legyen a polárszűrő síkjára!

  • Javaslat: Rakjon be egy lyukas papírt a fényútba, és ezen ellenőrizze, hogy a beeső és a visszavert sugár egybeesik-e!

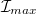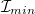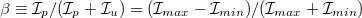Forgassa körbe a polárszűrőt, és mérje meg az \setbox0\hbox{$\mathcal{I}_{max}$}% \message{//depth:\the\dp0//}% \box0% maximális és az \setbox0\hbox{$\mathcal{I}_{min}$}% \message{//depth:\the\dp0//}% \box0% minimális fényintenzitást! Határozza meg a lézerfényben a lineárisan polarizált fény \setbox0\hbox{$\beta$}% \message{//depth:\the\dp0//}% \box0% arányát! \setbox0\hbox{$\beta \equiv \mathcal{I}_p/ ( \mathcal{I}_p + \mathcal{I}_u) = (\mathcal{I}_{max}-\mathcal{I}_{min})/(\mathcal{I}_{max}+\mathcal{I}_{min})$}% \message{//depth:\the\dp0//}% \box0%.

3. Állítsa be a polárszűrőt úgy, hogy a fényintenzitás maximális legyen! Szerelje fel a másik polárszűrőt is az optikai sínre és állítsa be ezt is a fénysugárra merőlegesen! Állítsa a második polárszűrő polarizációs irányát az elsővel párhuzamosra (forgassa addig, amíg a fényintenzitás maximális nem lesz)!

A 90° TN LC cella vizsgálata

4. Szerelje fel az NB 90° TN LC cellát (sárga drótok) a két polárszűrő közé, és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan!

  • Ügyeljen arra, hogy a lézersugár a cella közepén haladjon át, mert csak itt tudjuk a ráadott feszültséggel orientálni a molekulákat!

Forgassa körbe 5-10°-os lépésekben az LC cellát! Mérje meg, foglalja táblázatba és ábrázolja az áthaladó fény intenzitását a forgatás \setbox0\hbox{$\theta$}% \message{//depth:\the\dp0//}% \box0% szögének függvényében!

  • Miért változik a fényintenzitás?

5. Állítsa be úgy az LC cellát, hogy az intenzitás minimális legyen (NB mód)! Kapcsoljon a cellára 100 Hz-es négyszögjelet, és változtassa a jel (effektív) feszültségét 0-tól 7 V-ig!

  • Figyeljen arra, hogy a fontos, érdekes pontoknál megfelelően kis lépésekben változtassa a feszültséget!

Mérje meg, foglalja táblázatba és ábrázolja az NB 90° TN LC cella elektro-optikai kapcsolási görbéjét (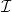\setbox0\hbox{$\mathcal{I}$}% \message{//depth:\the\dp0//}% \box0% az \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% függvényében)!

Határozza meg a 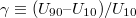\setbox0\hbox{$\gamma \equiv (U_{90}–U_{10})/U_{10}$}% \message{//depth:\the\dp0//}% \box0% kapcsolási meredekséget és az 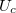\setbox0\hbox{$U_c$}% \message{//depth:\the\dp0//}% \box0% kritikus feszültséget! 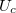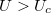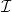\setbox0\hbox{$U_c$}% \message{//depth:\the\dp0//}% \box0% meghatározásánál vegye figyelembe, hogy \setbox0\hbox{$U > U_c$}% \message{//depth:\the\dp0//}% \box0% feszültségnél az \setbox0\hbox{$\mathcal{I}$}% \message{//depth:\the\dp0//}% \box0% fényintenzitás \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% monoton növekvő függvénye!

6. Párhuzamos polarizátor állás mellett forgassa a NB 90° TN LC cellát olyan pozícióba, melyben maximális az intenzitás. Mérje meg a cellára kapcsolt 100 Hz-es négyszögjel effektív feszültségének függvényében az intenzitás változását a 0-7 V tartományban!

  • Értelmezze a megfigyeléseket!

A párhuzamosan rendezett LC cella vizsgálata

7. Cserélje ki az NB 90° TN LC cellát a párhuzamosan rendezett cellával (narancssárga drótok), és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan!

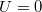  • A lézersugár ismét a cella közepén haladjon át! Egyelőre ne kapcsoljon feszültséget a cellára (\setbox0\hbox{$U = 0$}% \message{//depth:\the\dp0//}% \box0%)!

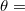Állítsa be a \setbox0\hbox{$\theta=$}% \message{//depth:\the\dp0//}% \box0% 45°-os elrendezést! Ehhez állítsa az analizátort a polarizátorral merőleges állásba (forgassa el 90°-kal), majd forgassa a párhuzamosan rendezett LC cellát addig, amíg az átmenő fény intenzitása el nem éri a maximális értékét (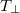\setbox0\hbox{$~T_\perp$}% \message{//depth:\the\dp0//}% \box0%)! Ez a helyzet valósítja meg a 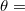\setbox0\hbox{$\theta=$}% \message{//depth:\the\dp0//}% \box0% 45°-os konfigurációt. Jegyezze fel a 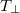\setbox0\hbox{$~T_\perp$}% \message{//depth:\the\dp0//}% \box0%-sel arányos intenzitásértékét! 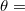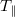Ezután mérje meg ugyanebben a \setbox0\hbox{$\theta=$}% \message{//depth:\the\dp0//}% \box0% 45°-os állásban az áteresztő képességet abban az esetben is, ha az analizátor és a polarizátor polarizációs iránya párhuzamos (\setbox0\hbox{$~T_\parallel$}% \message{//depth:\the\dp0//}% \box0%)!

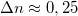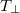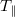Tudjuk, hogy a lézerfény hullámhossza 650 nm, az LC réteg vastagsága \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0% = 7,7 μm és hogy \setbox0\hbox{$\Delta n \approx 0,25$}% \message{//depth:\the\dp0//}% \box0%. Felhasználva \setbox0\hbox{$~T_\perp$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$~T_\parallel$}% \message{//depth:\the\dp0//}% \box0% az előzőek szerint megmért arányát, számítsa ki a 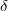\setbox0\hbox{$\delta$}% \message{//depth:\the\dp0//}% \box0% fáziskülönbség és a 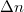\setbox0\hbox{$\Delta n$}% \message{//depth:\the\dp0//}% \box0% optikai anizotrópia pontos értékét az adott LC cellára, 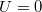\setbox0\hbox{$U = 0$}% \message{//depth:\the\dp0//}% \box0% esetében!

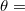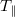8. Az előzőekhez hasonlóan, továbbra is a \setbox0\hbox{$\theta=$}% \message{//depth:\the\dp0//}% \box0% 45°-os konfigurációban mérjen! Kapcsoljon 100 Hz-es négyszögjelet a cellára és változtassa a feszültség (effektív) értékét 0-tól 7 V-ig! Mérje meg, foglalja táblázatba és ábrázolja a párhuzamos cella elektro-optikai kapcsolási görbéjét az analizátor és a polarizátor párhuzamos állásánál (\setbox0\hbox{$~T_\parallel$}% \message{//depth:\the\dp0//}% \box0%)!

  • A függvény szélsőértékeinek közelében vegye fel sűrűbben a pontokat (különösen a 0,5-4,0 V feszültségtartományban)!

Az elektro-optikai kapcsolási görbéből határozza meg a fázistolás mértékét 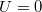\setbox0\hbox{$U = 0$}% \message{//depth:\the\dp0//}% \box0% feszültségnél!

  • Vesse össze az eredményt a 7. feladatban kapott eredménnyel!

Az elektro-optikai kapcsolási görbéből határozza meg azokat az 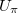\setbox0\hbox{$U_\pi$}% \message{//depth:\the\dp0//}% \box0% feszültségeket, amelyeknél az LC cellában a fázistolás 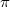\setbox0\hbox{$\pi$}% \message{//depth:\the\dp0//}% \box0% (180°)$!

  • Ne felejtse el, hogy 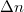\setbox0\hbox{$\Delta n$}% \message{//depth:\the\dp0//}% \box0% (és így 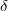\setbox0\hbox{$\delta$}% \message{//depth:\the\dp0//}% \box0% is) az \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% feszültség csökkenő függvénye!

Az elektro-optikai kapcsolási görbéből határozza meg azt a minimális \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% feszültséget, ahol a cellából kilépő fény cirkulárisan polarizált!

  • A fény akkor válik cirkulárisan polarizálttá, ha a fázistolás 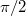\setbox0\hbox{$\pi/2$}% \message{//depth:\the\dp0//}% \box0% páratlan többszöröse.

A mérés végén ne felejtse el kikapcsolni a lézert, és kivenni az elemet a fotodetektorból!


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Folyadékkristályok_vizsgálata&oldid=13428”