„Spektrumanalízis heterodin méréstechnikával” változatai közötti eltérés
(→Bevezetés és történeti háttér) |
(→Bevezetés és történeti háttér) |
||
| 19. sor: | 19. sor: | ||
ahol $k_{\text{B}}$ a Boltzmann-állandó, $T$ az abszolút hőmérséklet és $\Delta f$ a sávszélesség. | ahol $k_{\text{B}}$ a Boltzmann-állandó, $T$ az abszolút hőmérséklet és $\Delta f$ a sávszélesség. | ||
| − | |||
*A ''Méréstechnika'' tárgyban tanultak szerint egy $R$ ellenálláson eső feszültség szórásnégyzete egy $\Delta f$ sávszélességű frekvenciaablakban mérve a termikus zaj miatt $\left< V^2 \right>=4 k_{\text{B}}T\Delta f$, így a termikus zaj teljesítménye $P=\left< V^2 \right>/R=4 k_{\text{B}}T\Delta f$. A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon. | *A ''Méréstechnika'' tárgyban tanultak szerint egy $R$ ellenálláson eső feszültség szórásnégyzete egy $\Delta f$ sávszélességű frekvenciaablakban mérve a termikus zaj miatt $\left< V^2 \right>=4 k_{\text{B}}T\Delta f$, így a termikus zaj teljesítménye $P=\left< V^2 \right>/R=4 k_{\text{B}}T\Delta f$. A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon. | ||
| − | + | Eszerint minél nagyobb az elvárt sávszélesség, annál nagyobb lesz a zaj teljesítménye is. A telekommunikációban a termikus zajteljesítmény nagyságára $P_{\text{vett zaj}}=k_{\text{B}}T\Delta f$ képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint 300 K hőmérsékleten a zajteljesítmény nagyságára $P_{\text{vett zaj}}(300\text{K})=k_{\text{B}}T\Delta f=4.1\cdot 10^{-21}\,\text{J} \cdot \Delta f$ adódik, ami egy 50 Ohmos ellenálláson körülbelül 1 nV feszültségnek felel meg 1 Hz sávszélesség mellett, illetve dBm egységekben $-174\,\text{dBm}\cdot 1\,\text{Hz}$. | |
| − | Eszerint minél nagyobb az elvárt sávszélesség, annál nagyobb lesz a zaj teljesítménye is. A telekommunikációban a termikus zajteljesítmény nagyságára $P_{\text{vett zaj}}=k_{\text{B}}T\Delta f$ képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint | + | *A dBm egység definíciója: $P[\text{dBm}]=10\cdot \log_{10}(P/1\text{mW}).$ |
A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés. | A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés. | ||
</wlatex> | </wlatex> | ||
A lap 2015. április 3., 05:42-kori változata
A mérési feladatot összeállította: Simon Ferenc és Halbritter András, BME Fizika Tanszék (2015)
A jegyzettel kapcsolatos javításokat, javaslatokat köszönettel kérjük az címre.
Bevezetés és történeti háttér
A laborgyakorlat célja, hogy a nagyfrekvenciás méréstechnikában széleskörben alkalmazott Fourier-analízis és heterodin méréstechnika alapjait bemutassa. A laborgyakorlat nagyban támaszkodik a korábbi Méréstechnika tárgyra, ezért az ott elsajátított ismeretek átismétlése elvárás.
Az adatátvitel alapfeladata, hogy a lehető legtöbb információt juttassunk el két pont között az információt minél jobban megtartva. Napjainkban amikor a környezetünk zsúfolva van különböző információtovábbító elektromágneses sugárzással, különösen fontos ez a kérdés. Az egyik elterjedt megoldás a különböző információk különböző frekvenciákhoz való rendelése (ún. frekvenciaosztásos multiplexelés). Ez eredményezi a manapság ismert különböző frekvenciájú rádióadások jelenlétét, ahol mindegyik rádiócsatorna adott (vivő)frekvencián sugározza az adását. Az adások információtartalma különböző módon van a vivőhullámba belekódolva. Itt a két legfontosabbat említjük csak, amivel a gyakorlaton is megismerkedünk: AM (amplitúdómoduláció) és FM (frekvenciamoduláció).
Belátható, hogy a továbbított információ mennyisége és az adott jelhez tartozó sávszélesség (
) egymással egyenesen arányos. Például egy állandó frekvenciájú sugárzással - melynek sávszélessége nulla - semmilyen információt nem tudunk továbbítani, de például egy 1 kHz frekvenciával modulált 100 MHz-es vivőhullámmal már tudunk 1 kbit/s információtovábbítást elérni. (Képzeljük el, hogy egy állandó frekvenciájú, időben állandó nagyságú elektromágneses jellel próbálunk információt közvetíteni. Ennek Fourier-transzformáltja egy Dirac-delta függvény, azaz nulla sávszélessége van. Azonban ennek a jelnek az információtartalma is nulla. A legegyszerűbb Morse-adatátvitelhez is már ki-be kell kapcsolgatnunk ezt a jelet, ami már természetesen nem lesz egy állandó frekvenciájú időben állandó nagyságú jel, és így a Fourier-transzformáltja sem lesz Dirac-delta.) Nem véletlen, hogy a hétköznapi gyakorlatban mindeki csak sávszélességről beszél mialatt a továbbított információ mennyiségére utal, miközben ez a fogalom alapvetően a továbbított jel frekvenciaspektrumának szélességére utal. Ebben a jegyzetben mi a hagyományos értelmeben vett (frekvencia-)sávszélességre utalunk.
Az emberi hang torzításmentes továbbításához (mono adás esetén) kb. 20 kHz sávszélességre van szükség. A gyakorlatban az egyes rádióadók frekvenciáját a zavaró interferencia elkerülésére végett ennél távolabbra állítják be, ezért találunk a mindenki által ismert FM sávban (87,5-108 MHz között) kb. 100 kHz-enként rádióállomásokat.
Egy másik gyakorlati megfontolás ami korlátozza az átvihető információ és így a sávszélesség nagyságát, az a zaj kérdése. A Méréstechnika tárgyban ismertetett módon az ún. Johnson-Nyquist vagy termikus zaj teljesítménye és a sávszélesség közötti kapcsolat:
![\[P_{\text{JN-zaj}}=4 k_{\text{B}}T\Delta f\]](/images/math/6/3/4/634a973a440068cc792e939eb2d83b23.png)
ahol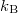 
a Boltzmann-állandó, 
az abszolút hőmérséklet és a sávszélesség.
- A Méréstechnika tárgyban tanultak szerint egy
ellenálláson eső feszültség szórásnégyzete egy sávszélességű frekvenciaablakban mérve a termikus zaj miatt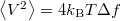 
, így a termikus zaj teljesítménye 
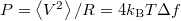. A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon.
Eszerint minél nagyobb az elvárt sávszélesség, annál nagyobb lesz a zaj teljesítménye is. A telekommunikációban a termikus zajteljesítmény nagyságára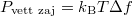 
képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint 300 K hőmérsékleten a zajteljesítmény nagyságára 
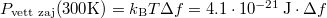adódik, ami egy 50 Ohmos ellenálláson körülbelül 1 nV feszültségnek felel meg 1 Hz sávszélesség mellett, illetve dBm egységekben 
.
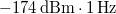- A dBm egység definíciója:
![\setbox0\hbox{$P[\text{dBm}]=10\cdot \log_{10}(P/1\text{mW}).$}% \message{//depth:\the\dp0//}% \box0%](/images/math/c/a/d/cada73ee7df8a16390c26128fefd9511.png)
A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés.
