„Zaj mint jel” változatai közötti eltérés
(→A zaj definíciója) |
(→Spektrumanalízis) |
||
| 61. sor: | 61. sor: | ||
A spektrumanalízisről szükséges részletes tudnivalók összefoglalója elérhető a Méréstechnika c. tárgy [[Spektrumanalízis szerkesztőlap]] fejezetéről készített szöveges összefoglalóban. | A spektrumanalízisről szükséges részletes tudnivalók összefoglalója elérhető a Méréstechnika c. tárgy [[Spektrumanalízis szerkesztőlap]] fejezetéről készített szöveges összefoglalóban. | ||
</wlatex> | </wlatex> | ||
| + | |||
===Aliasing jelenség=== | ===Aliasing jelenség=== | ||
<wlatex> | <wlatex> | ||
A lap 2019. február 7., 08:57-kori változata
A mérés célja
Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség "zaja" több információt hordoz a rendszerről, mint maga a várható érték [1]. A mérési gyakorlatok alkalmával különböző zajjelenségeket vizsgálunk egy mérőrendszer segítségével. Az első mérési alkalom során megismerkedünk a jelfeldolgozás alapjaival, majd ellenállások termikus zajának mérése alapján meghatározzuk a Boltzmann-állandó értékét. A második mérési alkalmon egy félvezető dióda zajának méréséből az elektrontöltés értékét határozzuk meg, majd megvizsgálunk egy 1/f jellegű zajspektrumot mutató rendszert.
Elméleti összefoglalás
A zaj definíciója
 |
| 1. ábra |
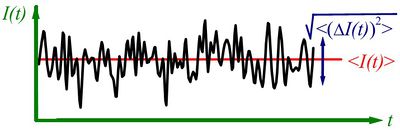
Egy időben változó mennyiség (pl.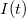 
áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, 
, illetve az átlagtól vett eltérést,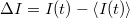 
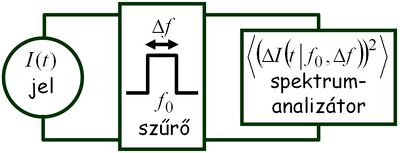
. A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével,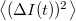 
, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az 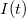jelet egy 
középfrekvencia körüli 
szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző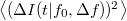 
szórásnégyzetet mérünk.
 |
| 2. ábra |
Az így kapott szórásnégyzet kis esetén arányos a sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
![\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]](/images/math/3/3/f/33ff88a562de7a830d972009efd5d850.png)
Áramzaj esetén az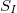 
spektrális sűrűség mértékegysége 
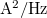. A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját 
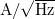mértékegységgel.
![\[\left<(\Delta V(t|f_0,\Delta f))^2\right>=S_V(f_0)\Delta f.\]](/images/math/8/9/a/89add176c6c234d68ca1a7b6097619e0.png)
Egy egyszerű ellenállás esetén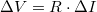 
, azaz 
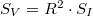. Egy nemlineáris eszköznél, pl. egy diódánál 
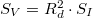, ahol 
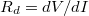az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
A fenti definíciók megismerése után érdemes megnézni a mérésnél használt Femto DLPVA 100-F-S típusú erősítő specifikációit, melyek szerint a műszer bemeneti zaja 80dB erősítés esetén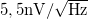 
. Ez azt jelenti, hogy az erősítő bemenetét rövidre zárva a várt zérus feszültség helyett az erősítő feszültségzaját látjuk, melynek a szórása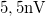 
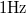-es sávszélességű mérés esetén.
Spektrumanalízis
Egy jel Fourier-transzformáltjának abszolútérték négyzetét a jel teljesítményspektrumának (Power Spectrum) nevezzük. A mérést 
diszkrét ponton végezve (Diszkrét Fourier-transzformáció, DFT), illetve beszorozva azt egy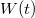 
ablakfüggvénnyel a kifejezés a következőképpen módosul:
![\[PS=|f_W(\omega)|^2=|\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.\]](/images/math/5/0/f/50f366f3f72a866eebfab2a5c8074cc3.png)
A feszültség szórásnégyzete a fentebb definiált zajsűrűség teljes frekvenciatartományra vett integráljával egyenlő.
![\[\langle(\Delta V(t))^2 \rangle=\int_{0}^{\infty} df s_V(f).\]](/images/math/4/e/5/4e5f54e003163e2b26ac0e5c132ede8d.png)
Másrészt megmutatható, hogy a feszültség átlagtól való eltérésének (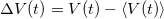
) a Fourier-transzformáltja abszolútértékének négyzete arányos a zajsűrűséggel. Mindez diszkrét mérési pontok esetén a következő formát ölti:
![\[s_V(\omega)\approx\frac{2}{N\Delta t}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2=\frac{2\Delta t}{N}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/6/0/3/603ab5b3fd96cfbcbb85edb29268c6af.png)
A fentiekben sikerült megállapítanunk, hogy a vizsgált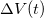 
jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk.
Nézzük meg, hogy egy tetszőleges ablakfüggvény esetén hogyan származtatható a zajsűrűség. Sajnos tetszőleges spektrumú zajra és tetszőleges ablakfüggvényre általános összefüggés nem adható, viszont ha 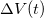fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor. Ekkor a zajsűrűség számolása:
![\[s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.\]](/images/math/9/1/7/917c7b49524f91ef5d3aee98385f13b5.png)
Diszkrét pontokon ugyanez a következő formában írható fel:
![\[s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}|\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.\]](/images/math/c/7/9/c798b690d1d9023a3a2741285d12ca1c.png)
A spektrumanalízisről szükséges részletes tudnivalók összefoglalója elérhető a Méréstechnika c. tárgy Spektrumanalízis szerkesztőlap fejezetéről készített szöveges összefoglalóban.
Aliasing jelenség
A DFT a mért jel spektrumát 
és 
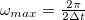frekvenciák közötti diszkrét pontokon értékeli ki. Felmerül a kérdés, hogy egy 
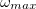-nál nagyobb frekvenciakomponenseket tartalmazó jelnél mi történik a magas frekvenciakomponensekkel.
Vizsgáljunk egy 
frekvenciájú tiszta szinuszos jelet:
![\[F(t)=A_0e^{i\omega_0t}.\]](/images/math/2/4/5/245b0442ddc0df9d07406191c01c8389.png)
Vegyük ennek a jelnek a Fourier-transzformáltját:
![\[f(\omega)=\int_{-\infty}^{\infty}A_0e^{i\omega_0t}e^{-i\omega t}dt=A_02\pi\delta(\omega-\omega_0).\]](/images/math/8/8/7/88791b26a657f44c0a4a149987bb78bc.png)
A jel Fourier-transzformáltja tehát a várakozásnak megfelelően egy Dirac-delta. Most nézzük meg, hogy a DFT számolása során hogyan változik a spektrum meghatározása a gyakorlatban.
![\[DFT(\omega_k)=\sum_{n=0}^{N-1}A_0e^{i\omega_0n\Delta t}W(n\Delta t)e^{-i\omega_k n\Delta t}\Delta t.\]](/images/math/7/7/4/77454b64a192deb67b7e8ea793f4485d.png)
Vegyük észre, hogy
![\[DFT(\omega_k)=DFT\left(\omega_k+\frac{2\pi m}{\Delta t}\right),\]](/images/math/f/d/3/fd376985dc4b0bb692451f12d2b4dc6c.png)
ahol 
egész szám. Másrészt
![\[DFT(\omega_k)=DFT^*(-\omega_k),\]](/images/math/5/e/6/5e6d6b14e0209e2955a599f2e5c37a67.png)
azaz
![\[\left|DFT(\omega_k)\right|=|DFT(-\omega_k)|.\]](/images/math/8/0/d/80ddbb4ed0ee9ca1958dfae37b6c7c3e.png)
Így belátható, hogy tetszőleges magas körfrekvenciájú jelet úgy látunk, mint ha az a ![\setbox0\hbox{$\left[0,\omega_{max}=\dfrac{2\pi}{2\Delta t}\right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/1/d/5/1d5edc142dda0da53e19be6704cd946e.png)
tartományban lévő jel lenne a saját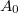 
amplitúdójával.
A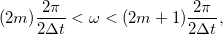 
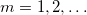frekvenciatartományokban lévő komponensek az 
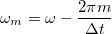frekvencián jelennek meg a spektrumban, míg a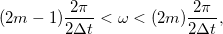 
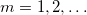tartományokban lévők a 
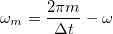frekvencián.
A fentiekkel beláttuk, hogy minden 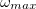-nál nagyobb frekvenciatag megjelenik a DFT-t követően a diszkrét frekvenciákat tartalmazó ![\setbox0\hbox{$[0,\omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/5/8/9/589da9a19c34b829d19740c9873851cf.png)
tartományban. Gondoljuk át, hogy a végeredményben kapott DFT spektrum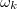 
pontjában összeadódnak-e a 
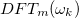tagok amplitúdói 
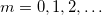értékekre. Mivel ezen frekvenciatagok fázisai nem azonosak, így a különböző értékekhez tartozó amplitúdók nem adhatóak össze.
Később látni fogjuk, hogy a zajsűrűség számításához a DFT abszolútérték négyzetére van szükség, amely azonban a véletlenszerű, egymástól független fázisok miatt egyenlő a különböző értékekre vett amplitúdók négyzeteivel:
![\[|DFT(\omega_k)|^2=\left(\sum_{m}^{} DFT_m(\omega_k)\right)\left(\sum_{m}^{} DFT^*_m(\omega_k)\right)=\sum_{m}^{}|DFT_m(\omega_k)|^2.\]](/images/math/1/7/b/17bbdbf920eb8fad23dd47b01b2d3d7f.png)
A leképezés leginkább úgy képzelhető el, mint a magas frekvenciás tartományok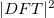 
-einek a intervallumra történő visszahajtogatása. Az 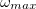fölötti részt visszahajtjuk ![\setbox0\hbox{$[-\infty; \omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/7/e/1/7e1583c668f4dc9fea3cf73d3c7fb0ab.png)
intervallumra. Majd ezt a visszahajtott spektrumot 0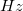 
-nél előrehajtjuk, stb. Ezt mindaddig folytatjuk, amíg minden jelentős frekvenciakomponenst be nem hajtottunk a intervallumba.
Beláttuk, hogy a magas komponensű jelek fals spektrumot okozhatnak, így gondoskodni kell kiszűrésükről egy aluláteresztő szűrővel. Ezt a jelenséget aliasingnak, azaz magas frekvenciájú komponensek beszűrődésének nevezzük. Fontos megjegyezni, hogy az aliasing kialakulásának az oka a DFT diszkrét mintavételezése, és független a mérési pontok számától. A gyakorlatban a legtöbbször az erősítők, vagy a mérőkártyák rendelkeznek anti-aliasing szűrővel, ami a maximális frekvencia fölött rendszerint élesen levágja a spektrumot.
Puskalövések zaja
A zaj fogalma egy klasszikus példával is jól szemléltethető, nézzük meg hogy mi történik ha egy puskából véletlenszerűen lövöldözünk, úgy hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő 
akkor 
idő alatt a lövések átlagos száma értelemszerűen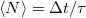 
. A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a 
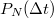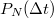valószínűséget, azaz annak a valószínűségét, hogy idő alatt lövés dördül. Ha értékét ismerjük, akkor 
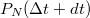értéke a
![\[P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)\]](/images/math/3/f/4/3f4062d58cc637d85054d98f2b6b3f49.png)
egyenlettel írható fel, azaz a kezdeti és az utána következő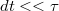 
idő alatt vagy 
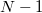ill. 
vagy ill. lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
![\[\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}\]](/images/math/b/6/4/b64ef404ea69d3816419cfebef01952b.png)
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a
![\[P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}\]](/images/math/f/b/b/fbb852541ecee469bb9e8e91c30241fe.png)
Poisson eloszlás elégíti ki. A Poisson eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz
![\[\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.\]](/images/math/c/9/2/c925d13d542008c08786e26fc2259b03.png)
Elektronok sörétzaja
A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot időbeli felbontással tudjuk mérni. Egy szélességű mintavételezési intervallum alatt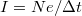 
áramot detektálunk ahol a idő alatt áthaladó eletronok számának eloszlását a fenti Poisson eloszlás adja meg. Így a mért áram várható értéke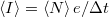 
, míg az áram szórásnégyzete 
.
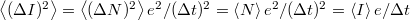Az eddigiekben feltettük, hogy a az az időtartomány, amelyen belül az elektronok számának várható értékes és szórásnégyzete megegyezik. Ha egy ilyen időablakra átlagolunk egy jelet, az a konvolúció egy olyan szűrőként viselkedik a frekvenciatérben, melyen keresztül fehér zajt mérve az áram szórásnégyzete egyenlő lesz egy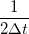 
tökéletes sávszűrőn mért szórásnégyzettel. Ennek a részletes levezetése a Méréstechnika tárgy Poisson zaj szerkesztőlap jegyzetében található.
Ez alapján az áram szórásnégyzete:
![\[\left< (\Delta I)^2 \right>=\int_0^{f_\mathrm{max}}S_I(f)df=2e\left< I \right>\cdot f_\mathrm{max},\]](/images/math/0/2/d/02d4546bad22d8b92bbfec96ba35ed53.png)
azaz:
![\[S_I=2e\left< I \right>.\]](/images/math/1/a/c/1ac0f27491897d7a5c456a1b44bb8271.png)
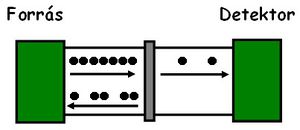
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt sörétzajnak szokták nevezni. Fontos megemlíteni, hogy a fenti képlet alapján a sörétzaj fehér zaj, azaz a spektrális sűrűség frekvenciafüggetlen. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli elv szerint két elektron nem lehet ugyan abban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkópikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább sorban egymást követve érkeznek az árammérőhöz, így a fenti zajformula nem érvényes. Azonban a Poisson zaj feltételét megvalósíthatjuk akkor, ha az elektronok útjába egy olyan akadályt helyezünk, melyen véletlenszerűen az elektronoknak csak egy kis része tud keresztüljutni (3a. ábra).
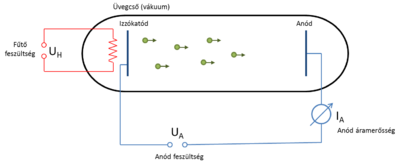
Az első sörétzaj-mérést Walter Schottky végezte 1918-ban [2]: híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 3b. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson zaj formulája alapján meghatározható.
 |
 |
| 3a. ábra | 3b. ábra |
Poisson zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén.
Termikus zaj
Az előbbiekben bemutatott sörétzaj egy nemegyensúlyi zaj, melyet csak akkor tapasztalunk, ha a vizsgált áramköri elemen áramot folyatunk keresztül. Zajt azonban egyensúlyi állapotban is tapasztalhatunk pusztán az elektronok termikus fluktuációi miatt. A termikus zaj megértése komolyabb elméleti hátteret igényel (részletes levezetés a Méréstechnika tárgy Termikus zaj szerkesztőlap jegyzeténél megtekinthető), azonban maga a jelenség egy nagyon egyszerű formulával leírható: egy 
elektromos ellenállással rendelkező áramköri elemen
![\[S_V=4k_B T\cdot R\]](/images/math/8/5/0/8500771d360277ebaf7f4f7c0a6fef77.png)
feszültségzaj-sűrűséget mérhetünk attól függetlenül, hogy pontosan milyen fizikai rendszer adja az ellenállást.
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
Ezen jelenség segítségével a 
hőmérséklet és az ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható.
1/f zaj
A termikus zaj és a sörétzaj mellett érdemes megemlékezni az 1/f zajról, mely a zajsűrűség tipikus 1/f jellegű frekvenciafüggéséről kapta a nevét. Ezen zajtípus számos fizikai folyamatból származhat, például a szennyezők és rácshibák véletlen mozgásából adódó ellenállásfluktuációkból. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség növelésével nő. Az 1/f zaj tipikusan alacsonyfrekvenciás (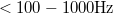
) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás.
Egyéb zajforrások
Az eddigiekben csak a vizsgált rendszerünk belső zajáról beszéltünk, azonban zajmérésnél mindig fontos a külső forrásokból adódó elektromágneses zavarokra is gondolni. Egy áramkör kapacitív vagy induktív csatolással könnyen felvesz zajt a környezetből például az elektromos hálózat 50 Hz-es frekvenciájánál, monitorok képernyőjének frissítési frekvenciájánál, kapcsoló üzemű tápok működési frekvenciájánál, vagy akár rádióállomások, mobiltelefonok sugárzási frekvenciájánál. Ezen zavaró tényezők kiküszöbölésének alapvető módszere a vizsgált áramkör árnyékolása: alacsony jelszintű méréseknél mindig árnyékolt kábeleket, illetve fém dobozba zárt áramköröket érdemes használni.
Mérési elrendezés
A méréshez használt eszközök
A méréshez egy NI myDAQ adatgyűjtő kártyát használunk használunk. A kártya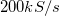 
sebességgel képes mintavételezni, illetve a továbbiak szempontjából fontos tulajdonsága, hogy nem rendelkezik anti-aliasing szűrűvel. Részletes specifikációk és leírás a műszer adatlapjában érhető el. A műszer analóg bemenetére egy BNC csatlakozót rögzítettünk a vizsgált rendszerek egyszerűbb csatlakoztatása céljából.
Az adatgyűjtő kártya USB porton keresztül csatlakozik a számítógéphez, ahol a jelet az NI ELVISmx programcsomagban található spektrumanalizátor (Dynamic Signal Analyzer) segítségével dolgozzuk fel. A program részletes használati útmutatása lentebb olvasható.
A magas komponensű jelek kiszűrése érdekében egy lezárható alumínium dobozban található harmadrendű RLC szűrőt használunk. A doboz oldalán lévő két BNC csatlakozó a be-, illetve kimenetet biztosítja.
Az alacsony zajszintek felerősítéséhez egy Femto DLPVA 100-F-S erősítőt használunk. Az erősítő kelezőfelülete a 4. ábrán látható. Az erősítő mindenképp erősít 20dB-t, majd AC/DC coupling között választhat a felhasználó, további 60dB (40dB+20dB) erősítés opcionális. Az erősítési tartomán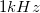y 
vagy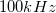 
közül választható. Méréseink során 80dB-es erősítést használjunk, és mindig figyeljünk oda, hogy ne kerüljön az erősítő overload-ba. Ezt egy piros LED égő kigyulladása jelzi..
 |
| 4. ábra |
Több mérési feladat során vizsgálunk, vagy használunk harmonikus jeleket, melyeket egy Agilent függvénygenerátorral adunk ki.
A termikus és a sörétzaj méréséhez egy lezárható alumínium dobozba helyezett panel áll rendelkezésre. A panelen levő csatlakozókba lehet bekötni a termikus zaj méréséhez használt R ellenállásokat és a sörétzaj méréséhez szükséges R1 és R2 ellenállásokat. (5. ábra). A dobozon három BNC csatlakozó és a tápfeszültség bekapcsolására szolgáló kapcsoló található. Rendelkezésre áll még egy további lezárható alumínium doboz az 1/f zaj mérésére. A dobozban található panelekbe kell bekötni a mérni kívánt rendszert és az áramérték meghatározására szolgáló feszültségosztó ellenállást. A dobozon a kivezetést biztosító BNC csatlakozó, illetve a tápfeszültség bekapcsolására szolgáló kapcsoló található. Kérjük győzödjön meg arról, hogy a mérőgyakorlat befejeztével a tápkapcsolókat kikapcsolt állapotban hagyta.
A méréshez különböző áramköri elemek állnak rendelkezésre: ellenállások, jumper, kondenzátorok, BNC-BNC toldó, BNC csatlakozós koax kábel.
A mérési összeállításban a mérni kívánt rendszert tartalmazó doboz megfelelő kimenetét közvetlenül az erősítőhöz csatlakoztatjuk egy BNC-BNC toldó segítségével, majd a felerősített jelet az aluláteresztő szűrőn keresztül a mérőkártyához csatlakoztatjuk a lehető legkevesebb BNC csatlakozós koax kábel segítségével. Bizonyos méréseknél az erősítőt és/vagy az aluláteresztő szűrőt kihagyjuk a mérési összeállításból, azonban ezt minden alkalommal jelezni fogjuk.
 |
| 5. ábra |
A termikus zaj mérésének elve
A termikus zaj mérésénél a doboz egyik BNC csatlakozójának belső pontja és földpontja közé egy ellenállást kötünk, a BNC csatlakozót pedig egy BNC-BNC toldó segítségével (lásd 4. ábra felső csatlakozó) közvetlenül az erősítő bemenetére kötjük és ebben az elrendezésben mérjük az ellenállás feszültségzaját. Mivel a mért termikus zaj összemérhető az erősítő bemeneti zajával (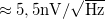
) ezért a mért zaj a termikus zaj és az erősítő bemeneti zajának összege lesz:
![\[S_V=4k_B T\cdot R + S_0.\]](/images/math/a/b/d/abd2e7c79dbc44dd178c08da8a388ecc.png)
Ha a mérést több ellenálláson is megismételjük akkor az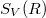 
függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann-állandó értékét, a tengelymetszetéből pedig az erősítő bemeneti zaját.
A sörétzaj mérésének elve
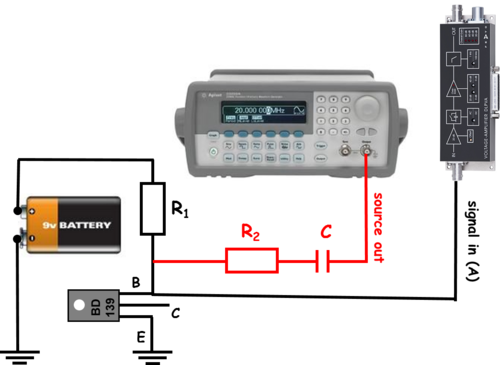
A sörétzaj mérésekor az 6. ábrán bemutatott kapcsolást érdemes alkalmazni. Tápegységként használjunk egy 9V-os elemet, így a meghajtó feszültségünk zaja kisebb lesz mint ha bármilyen elektromos hálózatra kötött tápegységet használnánk. A teleppel kössünk sorba egy nagy ellenállást (
) és egy félvezető diódát. Diódaként érdemes egy alacsony zajszintű tranzisztort használni úgy, hogy azt az 6. ábra szerint nyitó irányban a bázis és emitter kontaktusokon keresztül kötjük az áramkörbe és a kollektor elektródát nem használjuk.
 |
| 6. ábra |
A körben folyó egyenáramot könnyen meghatározhatjuk az ellenálláson eső feszültség mérése alapján (a biztonság kedvéért érdemes az ellenállás értékét is pontosan megmérni, és ezzel számolni a névleges érték helyett). A feszültség- és ellenállás-méréshez használjunk 4.5 digites Goodwill digitális multimétert.
Az áram meghatározása után mérjük meg a diódán jelentkező feszültségzajt. (Ennél a mérésnél az ábrán pirossal jelölt 
ellenállást és 
kondenzátort ne kössük az áramkörbe!) Az így mért feszültségzaj
![\[S_V=2e\left< I \right> \cdot R_d^2 +S_0,\]](/images/math/c/b/b/cbb0b32f6c711a3163b5c6a7e91a8bc6.png)
ahol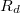 
a dióda differenciális ellenállása a beállított munkapontban, 
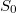pedig az erősítő bemeneti zaja.
A következő lépés a dióda differenciális ellenállásának* a meghatározása. Ehhez egy Agilent függvénygenerátorból egy ellenálláson és egy kondenzátoron keresztül váltóáramot keverünk a telepből jövő egyenáramhoz, és a mérőrendszerrel megmérjük a vátóáramú feszültségesést a meghajtó jellel azonos frekvencián. A függvénygenerátorból kiadott jel feszültségszintjét és az ellenállást úgy kell megválasztani hogy a diódán folyó váltóáram az egyenáramnál két nagyságrenddel kisebb legyen. A kapacitás azt a célt szolgálja, hogy a telepből jövő egyenáramból semennyi ne tudjon a függvénygenerátor kimenete felé elfolyni. Célszerű értékét úgy megválasztani hogy a meghajtó frekvencián vett impedancia lényegesen kisebb legyen -nél. Így a differenciális ellenállást
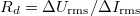képlet szerint számoljuk, ahol 
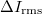a függvénygenerátorból kiadott váltófeszültség rms értékének (szórásának) és ellenállásnak a hányadosa,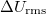 
pedig a diódán mért váltóáramú feszültség rms értéke.
Ha különböző ellenállásokkal megmérjük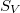 
, 
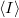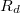és értékét akkor az 
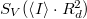függvényre egyenest illesztve megkapjuk az elektron töltésének értékét, míg az egyenes tengelymetszete megadja az erősítő bemeneti zajának értékét.
- A diódára kapcsolt egyenfeszültség egy állandó átfolyó áramot határoz meg, vagyis meghatározza a karakterisztika egy pontját, ezt nevezzük munkapontnak. A munkapontban tudjuk definiálni a dióda egyenáramú ellenállását, ami a rákapcsolt egyenfeszültség és az átfolyó áram hányadosa. A feszültség kis változtatásának (modulálás) hatása az áramra attól függ, hogy hol van a munkapont, hiszen a karakterisztika nemlineáris. A dióda differenciális (dinamikus) ellenállásának az adott munkaponti feszültség kis változását és a kialakuló áramváltozás hányadosát nevezzük.
Az 1/f zaj mérésének elve
A Dynamic Signal Analyzer használata és beállítása
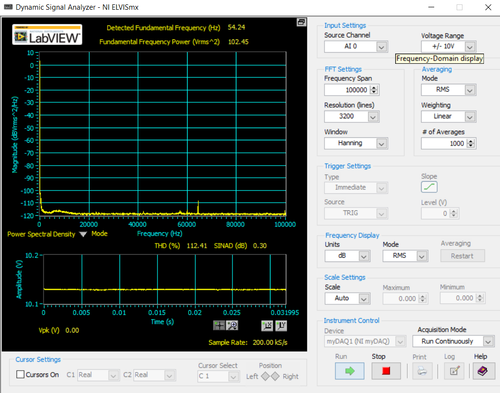
A Dynamic Signal Analyzer program az adatgyűjtő kártya bemenetén mért jel Fourier-spektrumát határozza meg. Kezelőfelületét a 7. ábrán láthatjuk.
 |
| 7. ábra |
- A program kijelzőjén láthatjuk a mért spektrumot dB-skálán, míg a frekvenciatengely felosztása lineáris. Ez alatt a kisebb kijelzőn a feszültség időfelbontása látható.
- A kijelző alatti legördülő menüben állítható be, hogy a jel komplex Fourier transzformáltját (teljesítményspektrum, Power Spectrum) vagy a zajsűrűség (PSD, Power Spectral Density) négyzetgyökét akarjuk mérni. Belátható hogy a PSD a Fourier transzformált abszolút érték négyzete megfelelő normálással.
- Az Input Settings menüben állítható be mintavételezési csatorna, illetve a mintavételezési tartomány. Ezek változtatására a laborgyakorlat során nincs szükség.
- Az FFT Settings menüben állítható be a maximális mintavételezési frekvencia (legfeljebb 100 kHz), a frekvenciapontok száma (Resolution), illetve a használni kívánt ablakfüggvény. PSD mérésnél a kis spektrális szivárgást adó Hanning ablakot, míg teljesítményspektrum mérésénél a jó amplitúdópontosságot mutató Flat Top ablakot célszerű használni.
- Az Averaging menüben állítható be az átlagolás módja, illetve az átlagolt eredmények súlyozása. Előbbi esetén négyzetes középértéket (rms), utóbbi esetén lineáris súlyozást használjunk. Szintén itt állíthatjuk be az átlagolt görbék számát, ezt celszerű legalább 1000-re választani.
- A Frequency Display menüben állíthatjuk be a kapott spektrum megtekintésének módját, itt javasoljuk a dB skálán való ábrázolást, illetve az RMS mód használatát.
- A Instrument Control menüben az Acquisition mode legördülő sávban választhatjuk ki, hogy folyamatos legyen a mintavételezés, vagy a beállított görbeszámot követően álljon le.
- A mintavételezést a Run gombbal indíthatjuk, míg a Stop gombbal állíthatjuk le. A Log gomb megnyomásával kiválaszthatjuk, hogy mely fájlba írja ki a program a legutóbb befejeződött mérés eredményét.
Mérési feladatok
1. Amplitúdópontosság meghatározása (első mérési alkalom)
Adjon a függvénygenerátorból rendre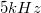 
, 
, 
, 
, 
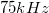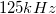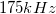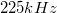és végül 
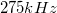frekvenciájú, 
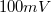amplitúdójú harmonikus jelet közvetlenül a mérőkártyára. Vizsgálja a teljesítményspektrumot (Power Spectrum) Flat Top ablakkal 
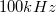-ig 3200 frekvenciaponton. Mit tapasztal? Számítással ellenőrizze, hogy a mért 
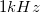-es komponens amplitúdója megegyezik a jelgenerátorból kiadott jel amplitúdójával!
2. Amplitúdópontosság mérése a mérési paraméterek függvényében (első mérési alkalom)
Állítsuk át az N frekvenciapontok számát az összes lehetséges értékere, és mérjük vissza ezekkel a beállításokkal egy 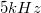frekvenciájú, 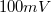amplitúdójú jel amplitúdópontosságát. Most állítsuk át a programunkat PSD mérésre, és használjunk Hanning ablakot. Ismételten vizsgáljuk, hogy különböző frekvenciafelbontásoknál milyen amplitúdót mérünk!
Szorgalmi feladat: Ismerve a Hanning-ablak ablakfüggvényét (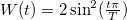
) számítsa ki a PSD mérés eredményéből a függvénygenerátorból kiadott jel amplitúdóját!
3. Az aluláteresztő szűrő átviteli karakterisztikájának meghatározása (első mérési alkalom)
A nagykomponensű jelek kiszűrése céljából használja a rendelkezésre álló aluláteresztő szűrőt! Határozza meg az aluláteresztő szűrő karakterisztikáját! Adjon ki a függvénygenerátorból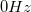 
és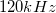 
között 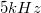-enként egy harmonikus jelet az aluláteresztő szűrőn keresztül a mérőkártyára. Határozza meg, hogy milyen tartományon értékelhetőek ki az eredményeink 1%-os pontossággal!
4. Az erősítő bemeneti zajának kísérleti meghatározása (első mérési alkalom)
Zárja az erősítő bemenetét rövidre, a kimenetét pedig az aluláteresztő szűrőn keresztül vezesse a mérőkártyára! Mérje meg az erősítő bemeneti zaját!
5. Külső zajok azonosítása (első mérési alkalom)
Azonosítsuk a spektrumban jelentkező nagyobb csúcsok forrását! Ehhez az áramkört körülvevő fém dobozt levett tetővel egy hosszabb koax kábelen keresztül csatlakoztassuk a spektrumanalizátorhoz, és a doboz mozgatása közben figyeljük meg, hogy hol nő illetve csökken a spektrumban megjelenő csúcsok amplitudója. A 0-100kHz-es frekvenciatartományban, N=3200 mellett egy mérési pont 31,25Hz szélességű tartománynak felel meg. Ilyen felbontású mérésnél bizonyos csúcsok beleolvadhatnak a fehérzaj háttérbe. Emiatt érdemes a spektrum különböző szűkebb tartományait lényegesen jobb frekvenciafelbontással is felvenni. Keressünk jellemző zaj-frekvenciákat a számítógép tápegységénél. a monitora körül, a multiméter közelében és értelmezzük azokat!
6. A Boltzmann-állandó meghatározása (első mérési alkalom)
Mérjük meg különböző ellenállások feszültségzaját, majd határozzuk meg a Boltzmann-állandó és az erősítő bemeneti zajának értékét!
A méréshez használjunk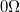 
-os ellenállást (rövidzár), illetve 
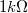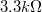-os, 
-os,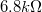 
-os és 
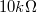-os ellenállásokat.
A spektrumot vegyük fel a teljes frekvenciatartományban (0-100kHz), és számoljunk egy átlagos spektrális sűrűséget. A mért spektrumból csak azokat a tartományokat vegyük figyelembe, ahol egyértelműen termikus zajra utaló fehérzajt látunk. Alacsony frekvencián ettől eltérést okozhat az 1/f zaj, magas frekvencián pedig a szűrő levágása. A spektrumban a környezetben elhelyezett műszerekre jellemző frekvenciáknál csúcsok jelenhetnek meg, ezeket ki kell hagyni az átlagos zajsűrűség számolásánál. A mérés során érdemes kiszámolni az adott ellenállásra várt zajsűrűség értékét, hiszen így rögtön észrevesszük ha például egy érintkezési hiba miatt téves értékeket mérünk.
7. Az elektron töltésének mérése (második mérési alkalom)
Állítsuk össze az 5. ábrán szemléltetett kapcsolást, és mérjük meg a BD139 tranzisztor feszültségzaját különböző ellenállásoknál, úgy hogy a diódán keresztül kb. 1, 3 és 10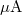
áram folyjon. (PSD mérés, Hanning ablak.) Az áram értékét mindig pontosan határozzuk meg az ellenálláson eső feszültség mérése alapján. A spektrumot 0-100kHz frekvenciatartományban mérjük. Válasszuk ki azt a frekvenciatartományt ahol már lecseng az alacsonyfrekvenciás 1/f zaj de még nem kezd el levágni a zajsűrűség az RC időállandók, vagy a szűrő levágása miatt.
Minden ellenállás-értéknél mérjük meg a dióda differenciális ellenállását. Ehhez a függvénygenerátorból kiadott ~1kHz-es váltóáramot keverjükk a 9V-os elemből jövő egyenáramhoz. A csatoló kondenzátor értéke 100nF, számítással igazoljuk, hogy az ellenállása elhanyagolható a kör összes ellenállása mellett. Az áramkör összeállítása előtt érdemes a kiadott jelet közvetlenül a mérőkártyára bemenetére kötni, és megmérni a kimeneti feszültséget. Ehhez a programmal PSD helyett Power Spectrum-ot mérjünk Flat Top ablakkal. Érdemes arra figyelni, hogy a kimeneti jel beállításánál amplitudót állítunk be, míg a Fourier spektrumban rms értéket mérünk.
Ha ezen tesztméréssel meggyőződtünk a műszer helyes beállításáról, akkor csatlakoztassuk az 5. ábrán pirossal jelölt áramköri részt és mérjük meg a differenciális ellenállások értékét. Figyeljünk arra, hogy a váltóáram kicsi maradjon az egyenáramhoz képest, érdemes a tranzisztoron jelentkező váltóáramú feszültséget 5mVrms alatt tartani.
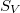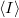A különböző értékeknél mért , és 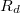értékek alapján határozzuk meg az elektron töltését és az erősítő bemeneti zaját.
8. 1/f zaj mérése (második mérési alkalom)
Kitekintés
A mérési gyakorlat keretében két - más mérésből jól ismert - fizikai állandó értékét mérjük meg zajmérés segítségével. Kutató laboratóriumokban azonban a zajmérést gyakran olyan területen alkalmazzák, ahol más mérési módszer csak korlátozottan, vagy egyáltalán nem áll rendelkezésre [1]. A következőkben ilyen mérésekből adunk rövid ízelítőt.
- A pontos hőmérsékletmérés - különösen extrém körülmények között - sokszor nehézséget jelent, hiszen számos fizikai folyamat (pl. fémek ellenállásváltozása, higanyszál megnyúlása) alkalmas a hőmérsékletváltozás detektálásra, azonban ezek a hőmérők az abszolút hőmérséklet mérésére csak pontos kalibráció után alkalmasak. Ezzel szemben a zajmérés segítségével közvetlenül az abszolút hőmérsékletet lehet meghatározni [3], így zajmérés megfelelő (a laborgyakorlat mérésénél lényegesen nagyobb) pontosság esetén akár hőmérsékletstandardként is használható.
- Az elektron töltését jól ismerjük, azonban számos olyan rendszer ismert ahol a kvázirészecskék az elektrontöltés többszörösét vagy tört részét hordozzák. Ezen rendszereknél a zajmérés kiválóan alkalmas a kvázirészecske-töltés meghatározására [4,5].
- Az elemi részecskék speciális statisztikákat követnek. Az elektronok például fermionként viselkednek, és a Pauli elv miatt két elektron nem lehet azonos kvantummechanikai állapotban, ezzel szemben a fotonok bosonként viselkednek, és szeretnek olyan állapotba szóródni amiben már több foton is található (lásd indukált emisszió a lézerekben). Ezen különbségek zajméréssel kiválóan kimutathatók, hiszen megfelelően megválasztott rendszerekben a fermionok a Poisson zajnál kisebb, míg a bosonok a Poisson zajnál nagyobb zajt mutatnak [6-8].
- A klasszikus és kvantumos kaotikus rendszerek jelentősen különböznek egymástól. A klasszikus káosz esetén ugyan a rendszer viselkedése érzékenyen függ a kezdeti feltételektől azonban mégis teljesen determinisztikus mozgást kapunk. Ezzel szemben kvantumkáosz esetén a részecskék viselkedése alapvetően véletlenszerű. A klasszikus és a kvantumkáosz közötti átmenet jól megmutatható zajmérésekkel, hiszen az előbbi esetben zérus, míg az utóbbiban véges sörétzajt várunk [9].
Zajmérésekkel részletesebben az Új kísérletek a nanofizikában tárgy keretében ismerkedhetünk meg.
Hivatkozások
[1] C. W. J. Beenakker, C. Schönenberger: Quantum shot noise, Physics Today 56, p37 (2003)
[5] R. de-Picciotto et al.: Direct observation of a fractional charge, Nature 389, p162 (1997)
[7] W.D. Oliver et al.: Hanbury Brown and Twiss-Type Experiment with Electrons, Science 284, p299 (1999)
[8] M. Henny et al.: The Fermionic Hanbury Brown and Twiss Experiment, Science 284, p296 (1999)
