„Rend és rendetlenség” változatai közötti eltérés
| 1. sor: | 1. sor: | ||
| − | [[Kategória: | + | [[Kategória:Szerkesztő:Vankó]] |
<wlatex> | <wlatex> | ||
Newton törvényeivel leírhatjuk makroszkopikus tárgyak mozgását a bolygóktól a biliárdgolyókig. Viszont egy kisebb szobában található mintegy <math>10^{27}</math> gázmolekula mozgását reménytelen, és értelmetlen egyenként követni. Szerencsére a statisztikus fizika segítségével a nagyszámú részecske átlagos jellemzői (pl. hőmérséklet, nyomás) közötti összefüggéseket pontosan megérthetjük. A statisztikus fizika számos komplex rendszer leírására is alkalmas, a természetben előforduló érdekes mintaképződésektől az internet vagy pénzügyi folyamatok modellezésén keresztül a kollektív mozgások (pl. közlekedési dugók) megértéséig. Ezen komplex folyamatok megértésében a statisztikus fizikán alapuló számítógépes szimulációknak kiemelkedő jelentősége van. | Newton törvényeivel leírhatjuk makroszkopikus tárgyak mozgását a bolygóktól a biliárdgolyókig. Viszont egy kisebb szobában található mintegy <math>10^{27}</math> gázmolekula mozgását reménytelen, és értelmetlen egyenként követni. Szerencsére a statisztikus fizika segítségével a nagyszámú részecske átlagos jellemzői (pl. hőmérséklet, nyomás) közötti összefüggéseket pontosan megérthetjük. A statisztikus fizika számos komplex rendszer leírására is alkalmas, a természetben előforduló érdekes mintaképződésektől az internet vagy pénzügyi folyamatok modellezésén keresztül a kollektív mozgások (pl. közlekedési dugók) megértéséig. Ezen komplex folyamatok megértésében a statisztikus fizikán alapuló számítógépes szimulációknak kiemelkedő jelentősége van. | ||
A lap 2011. május 12., 15:53-kori változata
Newton törvényeivel leírhatjuk makroszkopikus tárgyak mozgását a bolygóktól a biliárdgolyókig. Viszont egy kisebb szobában található mintegy 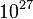 gázmolekula mozgását reménytelen, és értelmetlen egyenként követni. Szerencsére a statisztikus fizika segítségével a nagyszámú részecske átlagos jellemzői (pl. hőmérséklet, nyomás) közötti összefüggéseket pontosan megérthetjük. A statisztikus fizika számos komplex rendszer leírására is alkalmas, a természetben előforduló érdekes mintaképződésektől az internet vagy pénzügyi folyamatok modellezésén keresztül a kollektív mozgások (pl. közlekedési dugók) megértéséig. Ezen komplex folyamatok megértésében a statisztikus fizikán alapuló számítógépes szimulációknak kiemelkedő jelentősége van.
gázmolekula mozgását reménytelen, és értelmetlen egyenként követni. Szerencsére a statisztikus fizika segítségével a nagyszámú részecske átlagos jellemzői (pl. hőmérséklet, nyomás) közötti összefüggéseket pontosan megérthetjük. A statisztikus fizika számos komplex rendszer leírására is alkalmas, a természetben előforduló érdekes mintaképződésektől az internet vagy pénzügyi folyamatok modellezésén keresztül a kollektív mozgások (pl. közlekedési dugók) megértéséig. Ezen komplex folyamatok megértésében a statisztikus fizikán alapuló számítógépes szimulációknak kiemelkedő jelentősége van.
Tartalomjegyzék |
Mikroszkopikus és makroszkopikus leírás
A hőmérséklet kinetikus értelmezése
Egy egyensúlyban lévő rendszer állapotát jellemezhetjük a makroszkopikus állapotjelzőkkel. Az állapotjelzők csak a rendszer pillanatnyi állapotától függenek, függetlenek a rendszer előéletétől. Az extenzív állapotjelzők a rendszer méretével együtt nőnek, két rendszer egyesítésekor összeadódnak: ilyen pl. a térfogat, a tömeg, a mólszám, a belső energia és az entrópia. Az intenzív állapotjelzők – pl. a hőmérséklet, a nyomás, a kémiai potenciál és a sűrűség – a rendszer méretétől függetlenek, két rendszer egyesítésekor átlagolódnak.
A hőmérséklet értelmezéséhez több lépésben juthatunk el. A fogalom a hétköznapi tapasztalatból származik: érzékszerveinkkel meg tudunk különböztetni hideg és meleg testeket. Az érzékelés azonban meglehetősen szubjektív: például ugyanazt a langyos vizet melegnek vagy hidegnek fogjuk érezni attól függően, hogy előtte a kezünk hideg vagy forró vízben volt-e. A hőmérséklet objektív mérését az teszi lehetővé, hogy az anyagok számtalan tulajdonsága hőmérsékletfüggő. A hagyományos higanyos vagy alkoholos hőmérőkben a folyadékok hőtágulása, az elektromos hőmérőkben pedig legtöbbször az anyagok hőmérsékletfüggő fajlagos ellenállása alapján mérjük a hőmérsékletet.
A hétköznapi életben a hőmérséklet méréséhez a Celsius-skálát használjuk, melynek két rögzített pontja a víz fagyáspontja (0 °C) és a víz forráspontja normál légköri nyomáson (100 °C). A fizikában a hőmérséklet mértékegysége a kelvin (K): a termodinamikai (vagy abszolút) hőmérsékleti skála egysége megegyezik a Celsius-skála egységével, de nullpontja az un. abszolút nulla fok (-273,15 °C = 0 K).
Az állapotjelzők nem függetlenek egymástól, különböző rendszereknél más-más kapcsolat írható fel közöttük. A valóságos rendszereket különböző modellekkel lehet leírni. Egyszerűsége, elméleti és gyakorlati jelentőssége miatt is kiemelkedő fontosságú modell az ideális gáz. Az ideális gáz modellben a molekulák között – az ütközéseket kivéve – nincs kölcsönhatás, és a molekulák össztérfogata sokkal kisebb, mint a tartály térfogata. A hétköznapi életben a nem túl nagy sűrűségű gázok jó közelítéssel ideális gáznak tekinthetők.
Az ideális gáz makroszkopikus állapotjelzői között a tapasztalat szerint a![\[pV=nRT\]](/images/math/c/6/3/c634efd95a0753d59c8f23bd97bb3ee6.png)
kapcsolat írható fel, ahol  a gáz nyomása,
a gáz nyomása,  a térfogata,
a térfogata,  a mólszám,
a mólszám,  az abszolút hőmérséklet és
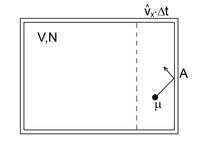
az abszolút hőmérséklet és  = 8,314 J/molK az egyetemes gázállandó. A gáz nyomása (a tartály falának egységnyi területű darabjára ható erő) a tartály falának ütköző, és onnan visszaverődő molekulák impulzusváltozásából ered. A gáz homogén és izotróp, így a molekulák egyforma valószínűséggel haladnak minden irányba. A gázmolekulák nem egyforma sebességgel mozognak (sebességeloszlásukat a Maxwell-eloszlás adja meg), de számításunkban csak a sebességek négyzetes középértékére (
= 8,314 J/molK az egyetemes gázállandó. A gáz nyomása (a tartály falának egységnyi területű darabjára ható erő) a tartály falának ütköző, és onnan visszaverődő molekulák impulzusváltozásából ered. A gáz homogén és izotróp, így a molekulák egyforma valószínűséggel haladnak minden irányba. A gázmolekulák nem egyforma sebességgel mozognak (sebességeloszlásukat a Maxwell-eloszlás adja meg), de számításunkban csak a sebességek négyzetes középértékére (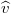 ) van szükség.
) van szükség.
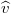 négyzetes középsebességgel mozogna. A Pitagorasz-tétel alapján
négyzetes középsebességgel mozogna. A Pitagorasz-tétel alapján ![\[\widehat{v}^2=\widehat{v}_x^2+\widehat{v}_y^2+\widehat{v}_z^2=3\widehat{v}_x^2\]](/images/math/d/a/f/daf4a204af75256dfa452ed5dcf4cd2a.png)
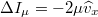 , ahol
, ahol  a molekula tömege. A falat
a molekula tömege. A falat  idő alatt azok a részecskék érik el, amelyek legfeljebb
idő alatt azok a részecskék érik el, amelyek legfeljebb 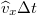 távolságra vannak a faltól, és a fal felé mozognak. Ezek száma
távolságra vannak a faltól, és a fal felé mozognak. Ezek száma ![\[\Delta N=\frac{N}{2}\frac{\widehat{v}_x\Delta t A}{V}\]](/images/math/9/e/2/9e295b66542b1ee3c4630ae5e9826021.png)
 az összes részecske száma (a szimmetria miatt ezek fele mozog a fal felé). A falra ható erő
az összes részecske száma (a szimmetria miatt ezek fele mozog a fal felé). A falra ható erő ![\[F=-\frac{\Delta I}{\Delta t}=\frac{N}{2}\frac{\widehat{v}_x\Delta t A}{V}\frac{2\mu\widehat{v}_x}{\Delta t}=\frac{\mu\widehat{v}_x^2 N A}{V}=\frac{\mu\widehat{v}^2 N A}{3V}\]](/images/math/b/6/5/b65ffd64fcdc3ac7a961b2046a62df1b.png)
![\[p=\frac{F}{A}=\frac{2}{3}\frac{1}{2}\mu\widehat{v}^2\frac{N}{V}=\frac{2}{3}\bar{\varepsilon}_h\frac{N}{V}\]](/images/math/9/d/8/9d80cfca9375164b38b099aaf8c079a8.png)
![\[\bar{\varepsilon}_h=\frac{1}{2}\mu\widehat{v}^2\]](/images/math/a/3/c/a3cc12549265436ac91a0acecb5fb5de.png)
a molekulák átlagos haladó mozgási energiája.
Az eredményt összevethetjük az ideális gáz állapotegyenletével:![\[pV=\frac{2}{3}\bar{\varepsilon}_h N=nRT\]](/images/math/a/d/8/ad8e795c8757311e2e05574ba26cec42.png)
![\[\bar{\varepsilon}_h=\frac{3}{2}\frac{n}{N}RT=\frac{3}{2}\frac{R}{L}T=\frac{3}{2}kT\]](/images/math/9/4/4/9442d8cd1feaef1f9e51a2d4be55471d.png)
![\[L=6,02\cdot 10^{23}\,{\rm 1/mol}\]](/images/math/2/6/3/263eb3fef80105903acab2ab40171089.png)
![\[k=\frac{R}{L}=1,38\cdot 10^{-23}\,{\rm J/K}\]](/images/math/5/8/d/58dbdb3f9f2086af58c698d1a275c4c7.png)
![\[\widehat{v}=\sqrt{\frac{3kT}{\mu}}=\sqrt{\frac{3RT}{M}}\]](/images/math/4/7/0/4705d932eefe330cc87b800362647ca8.png)
ahol  a moláris tömeg. Szobahőmérsékletű nitrogén esetében az átlagos sebesség kb. 500 m/s.
a moláris tömeg. Szobahőmérsékletű nitrogén esetében az átlagos sebesség kb. 500 m/s.
Ezek az összefüggések kapcsolatot teremtenek a mikroszkopikus állapotjelzők (molekulák átlagos sebessége, átlagos mozgási energiája) és a makroszkopikus állapotjelzők (nyomás, hőmérséklet) között.
A hőtan I. főtétele
Belső energia
Egy rendszer belső energiája a benne lévő részecskék tömegközépponthoz viszonyított mozgási energiájának és a részecskék közti erőkből származó potenciális energiának az összege. Mozgási energia a szabadon mozgó részecskék haladó mozgásából, a molekulák forgásából és belső rezgéséből, illetve szilárd anyagoknál az atomok és molekulák rácshely körüli rezgéséből származik.
Az ideális gázban a molekulák közt (az ütközéseket kivéve) nincs kölcsönhatás, így a potenciális energia nulla. A mozgási energia az egyes atomok mozgási energiájának összege. Egyatomos molekulák (nemesgázok) esetében a molekuláknak csak haladó mozgási energiája van. (Az atomok tömegének 99,8 %-a az atomnál 5 nagyságrenddel kisebb átmérőjű atommagban van, így az pontszerűnek tekinthető.) Kétatomos (és többatomos lineáris molekulák) a molekula tengelyére merőleges két tengely körül, többatomos térbeli molekulák pedig három tengely körül foroghatnak, amelyhez szintén mozgási energia („forgási energia”) tartozik.
Az ekvipartíció tétele szerint minden szabadsági fokra átlagosan ugyanakkora energia jut. Az egyatomos gázban a molekuláknak 3 szabadsági foka van (3 dimenzióban mozoghat), a kétatomos gázban 5 (3 a haladó mozgásból + 2 a két tengely körüli forgásból), a többatomos gázokban pedig 6 (3 haladó + 3 forgó mozgásból). Nagyobb molekuláknál, vagy magasabb hőmérsékleten a molekulák rezgéseihez is tartozhat szabadsági fok. Az ekvipartíció tétele nem csak gázokra, hanem más rendszerekre is igaz: a szilárd testek rezgő atomjainak például 6 szabadsági foka van (3 mozgási energia + 3 potenciális energia tagból).
Az egyatomos gázban a molekulák átlagos mozgási energiája![\[\bar{\varepsilon}_m=\bar{\varepsilon}_h=\frac{3}{2}kT\]](/images/math/e/e/d/eed7ad06af88f21415585c39b3ebef04.png)
![\[\bar{\varepsilon}_0=\frac{1}{2}kT\]](/images/math/4/0/e/40e3f6e494c30696b7f7f47b56e52543.png)
 szabadsági foka van, akkor a molekula átlagos mozgási energiája
szabadsági foka van, akkor a molekula átlagos mozgási energiája ![\[\bar{\varepsilon}_m=\frac{f}{2}kT\]](/images/math/d/9/5/d9562fdb13904d66b71220ef6a3c4431.png)
![\[E=N\bar{\varepsilon}_m=\frac{f}{2}NkT=\frac{f}{2}nRT\]](/images/math/2/3/9/2395133c47abd5d0780c0b2271642389.png)
A belső energia az ideális gáznál tehát csak a hőmérséklettől függ. Más anyagoknál a belső energia a többi állapotjelzőtől is függhet (lásd pl. Van der Waals-gáz).
Munkavégzés és hőközlés
A rendszer belső energiája csak akkor változhat meg, ha a rendszer a környezettől energiát kap vagy a környezetnek energiát ad le. Az energiaátadásnak két lényegesen különböző módja van: a munkavégzés és a hőközlés.
Ha a rendszer kitágul, akkor a környezetén munkát végez. A rendszer összenyomásához viszont külső munkavégzés szükséges (ilyenkor a rendszer munkavégzése negatív). Az elemi munkavégzés![\[{\rm d}W=p{\rm d}V\]](/images/math/f/0/d/f0d84d5395aaa08a4f319f15a3a5078b.png)
![\[W=\int_1^2 p{\rm d}V\]](/images/math/1/0/3/1039180fecc7eb62bb73720cedfaa51f.png)
A munkavégzés az energiaátadás „rendezett” módja: pl. a tartályt elzáró dugattyú valamilyen irányban elmozdul. (A munkavégzés az elmozdulás irányától függően pozitív vagy negatív lehet.) Bár mechanikai elmozdulás nem történik, termodinamikai szempontból munkavégzés a termoelemben keletkező elektromos munka, illetve a Peltier-elemben a rendszerrel közölt elektromos munka is.
A hőközlés az energiaátadás „rendezetlen” módja: úgy jön létre energiaátadás, hogy a két rendszer (vagy a rendszer és környezete) hőmozgásban lévő részecskéi véletlenszerű ütközésekkel adnak át energiát egymásnak. A tapasztalat szerint azonban a magasabb hőmérsékletű rendszer (átlagosan nagyobb energiájú) részecskéi az ütközések során átlagosan több energiát adnak át az alacsonyabb hőmérsékletű (átlagosan kisebb energiájú) részecskéinek, mint viszont. Emiatt ez az energiaátadási forma meghatározott irányú: mindig a melegebb test ad át energiát a hidegebb testnek. A hőközléskor a rendszer által felvett energiát (a „hőt”)  -val jelöljük.
-val jelöljük.
![\[\Delta E=Q-W\]](/images/math/2/3/0/2307dd275da59a1f960d1cfeaf3d3e7e.png)
Az I. főtétel azt is kifejezi, hogy az energiaátadásnak két lényegesen különböző módja van. (A munkavégzés előtt azért van negatív előjel, mert 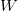 a rendszer által végzett munka.)
a rendszer által végzett munka.)
A hőtan II. főtétele
Hőerőgép, hőszivattyú, hűtőgép
Az I. főtétel szerint egy rendszer belső energiája hőközléssel és munkavégzéssel is megváltoztatható. Ez lehetővé teszi olyan berendezések készítését, melyek hőközlés hatására mechanikai munkát végeznek (hőerőgép), illetve mechanikai munka segítségével hidegebb helyről a melegebb felé hoznak létre hőtranszportot (hőszivattyú, hűtőgép).
A járművekben használt benzin- és dízelmotorok, a gőzgépek, az atom- és hőerőművekben használt gőz- és gázturbinák, a repülőgépek sugárhajtóműve mind hőerőgépek: különböző anyagok elégetése vagy az urán hasadása közben felszabaduló hőt alakítják (részben) mechanikai munkává – amely a járművekben közvetlenül hasznosul, az erőművekben pedig az elektromos energiát előállító generátorokat működteti. A különböző hőerőgépekben különböző termodinamikai folyamatok játszódnak le, és más-más technikai megoldásokat alkalmaznak, de a hőerőgépek lényegét egyszerűbb modelleken is megérthetjük.
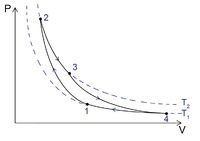
Ha vizet forralunk (hőt közlünk vele), akkor a felszabaduló vízgőz térfogata megnő, és eközben munkát végez. Ez egy nagyon egyszerű hőerőgép. Azonban ahhoz, hogy a berendezés folyamatosan működjön, a vizet is folyamatosan pótolni kell, vagy a keletkező és kitáguló vízgőzt kell visszaalakítani vízzé. Ilyen módon ciklikusan működő berendezést hozhatunk létre. A víz-vízgőz rendszer viselkedésének leírása a halmazállapot-változás miatt bonyolultabb, azonban hőerőgép ideális gázon végzett körfolyamatok segítségével is létrehozható. Ezek közül elméleti szempontból a Carnot-ciklus a legfontosabb. A 2. ábrán p-V állapotsíkon ábrázolt körfolyamat négy részből áll:
Az 1-2 folyamat egy adiabatikus összenyomás. A külvilágtól hőszigeteléssel elválasztott gázt külső munkavégzéssel összenyomjuk – ennek hatására a belső energiája, és így a hőmérséklete is megnő.
A 2-3 folyamat egy izoterm kitágulás. A gáz a (legalább) 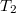 hőmérsékletű környezettől („kazán”) hőt vesz fel, eközben kitágul, és munkát végez. A belső energiája (és így a hőmérséklete) nem változik, mert a felvett hő és a munkavégzés nagysága megegyezik.
hőmérsékletű környezettől („kazán”) hőt vesz fel, eközben kitágul, és munkát végez. A belső energiája (és így a hőmérséklete) nem változik, mert a felvett hő és a munkavégzés nagysága megegyezik.
A 3-4 folyamat egy adiabatikus kitágulás. A gáz ismét a külvilágtól elzárt (hőcsere nincs), a munkavégzés miatt csökken a belső energia és a hőmérséklet. Bebizonyítható, hogy a gáz munkavégzése éppen ugyanakkora, mint az 1-2 folyamatban a gázon végzett munka, így ez a két folyamat egymást kiegyenlíti, a további számításokból kihagyható. (Csak azért van rájuk szükség, hogy a gáz átjusson egyik izotermáról a másikra.)
A 4-1 folyamatban a gázt vissza kell juttatni a kiinduló állapotba, hogy a folyamat zárt, ciklikusan ismételhető legyen. Ez egy izoterm összenyomás: a gázt külső munkavégzéssel össze kell nyomni, miközben az így nyert belső energiát a (legfeljebb)  hőmérsékletű környezetnek („hűtő”) leadja.
hőmérsékletű környezetnek („hűtő”) leadja.
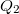 hőt, a hidegebb környezetnek (a „hűtő”-nek) pedig lead
hőt, a hidegebb környezetnek (a „hűtő”-nek) pedig lead 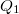 hőt. A kettő különbsége a hőerőgép által végzett hasznos munka (a kitágulás közben végzett munka és az összenyomáshoz felhasznált munka különbsége):
hőt. A kettő különbsége a hőerőgép által végzett hasznos munka (a kitágulás közben végzett munka és az összenyomáshoz felhasznált munka különbsége): ![\[W=Q_2-Q_1\]](/images/math/0/1/f/01f246c576b3992d212a4f9d8c19ecc5.png)
![\[\eta=\frac{W}{Q_2}=\frac{Q_2-Q_1}{Q_2}=1-\frac{Q_1}{Q_2}\]](/images/math/e/7/a/e7a2fe9dbecefb08a12197a517652ec8.png)
![\[\frac{Q_1}{Q_2}=\frac{T_1}{T_2}\]](/images/math/6/a/e/6ae0d68a20a3bde772b561e2e297e5b8.png)
![\[\eta=1-\frac{T_1}{T_2}\]](/images/math/9/4/c/94cf63c242eee8b0948ea8d1c2ee0340.png)
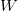 ) hatására
) hatására 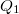 hőt von el a hidegebb (
hőt von el a hidegebb ( ) hőmérsékletű környezettől, és
) hőmérsékletű környezettől, és 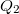 hőt ad le a melegebb (
hőt ad le a melegebb (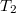 ) hőmérsékletű környezetnek. A magasabb hőmérsékleten leadott hő a hidegebb környezettől felvett hő és a befektetett munka összege:
) hőmérsékletű környezetnek. A magasabb hőmérsékleten leadott hő a hidegebb környezettől felvett hő és a befektetett munka összege: ![\[Q_2=Q_1+W\]](/images/math/f/9/7/f97b2b01482926768a5758d9b199cec6.png)
Ez a folyamat a hőszivattyú és a hűtőgép modellje (a valódi berendezések ennél bonyolultabb folyamatokkal működnek).
Hőszivattyúval a külső (hidegebb) környezettől elvont hő felhasználásával lehet fűteni, így a berendezés teljesítménytényezője 1-nél nagyobb:![\[\varepsilon=\frac{Q_2}{W}=\frac{Q_1+W}{W}=1+\frac{Q_1}{W}\]](/images/math/6/1/4/61423de2ebce90a14157466f0fa7c19e.png)
A hűtőgép hőt von el egy a környezeténél hidegebb helyről, és azt (a befektetett munkával együtt) leadja a melegebb környezetnek. Ezért meleg a hűtőgép hátulja.
A II. főtétel néhány megfogalmazása
Az I. főtétel kimondja, hogy energia nem keletkezhet (és nem tűnhet el). Ezzel korlátozza a lehetséges folyamatok körét, például kizárja az örökmozgó – az elsőfajú perpetuum mobile, egy olyan berendezés, amely a környezettől elzárva folyamatosan energiát termel – létét. Ugyanakkor az I. főtétel semmit nem mond a lehetséges folyamatok irányáról.
A tapasztalat szerint viszont bizonyos folyamatok csak kitüntetett irányban mennek végre. Ha például forró vízbe jeget dobunk, akkor az „magától” elolvad, és langyos víz keletkezik. Ugyanakkor a magára hagyott langyos vízből nem lesz külső behatás nélkül újra jég és forró víz (annak ellenére, hogy az I. főtétel ezt nem tiltaná).
A termodinamika II. főtétele a folyamatok irányát határozza meg. Sokféleképp megfogalmazható, ezek közül néhány (és majd kicsit később egy további is):
A hőátadás spontán (külső hatás nélkül) mindig a melegebb testről a hidegebb felé történik.
Az intenzív állapotjelzők különbségei (hőmérsékletkülönbség, nyomáskülönbség, kémiai potenciál különbség) idővel mindig a kiegyenlítődés felé változnak.
Egy (ciklikus folyamattal működő) hőerőgép termikus hatásfoka soha nem lehet 1, azaz egy rendszer belső energiája nem alakítható teljes egészében mechanikai munkává. (Nem készíthető másodfajú perpetuum mobile sem.) A valóságos hőerőgépek hatásfoka nem lehet jobb, mint a Carnot-gép termikus hatásfoka. Így![\[\eta\leq 1-\frac{T_1}{T_2}<1\]](/images/math/d/f/6/df60cbe4f5233e794ec252a971ab6882.png)
ahol  és
és 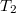 a gép működéséhez használt hideg és meleg környezet („hőtartály”) hőmérséklete. A hőerőgép működtetéséhez két különböző hőmérsékletű hőtartály szükséges.
a gép működéséhez használt hideg és meleg környezet („hőtartály”) hőmérséklete. A hőerőgép működtetéséhez két különböző hőmérsékletű hőtartály szükséges.
Peltier-elem: a számítógépben használt hűtőgép
Hőerőgépek és hűtőgépek nem csak gázok összenyomásával és kitágulásával működhetnek. A termoelektromos jelenségek lehetővé teszik mozgó alkatrésze nélküli, közvetlenül elektromos energiát termelő, illetve elektromos energiával működő eszközök készítését.
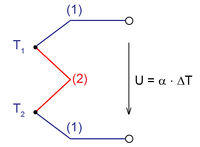
Két különböző fém, vagy különböző félvezető anyag érintkezésénél potenciálkülönbség alakul ki. Ez a potenciálkülönbség hőmérsékletfüggő, ezért ha a 3. ábrán látható elrendezésben a két érintkezési pont hőmérséklete különböző, a kimeneteken elektromos feszültség jelenik meg (Seebeck-effektus). A feszültség arányos a két érintkezési pont hőmérsékletkülönbségével:
elektromos feszültség jelenik meg (Seebeck-effektus). A feszültség arányos a két érintkezési pont hőmérsékletkülönbségével: ![\[U=\alpha\Delta T\]](/images/math/b/b/3/bb3f8aad6e0e5ab6b40565c8dc34be42.png)
ahol  az anyagpárra jellemző Seebeck-együttható.
az anyagpárra jellemző Seebeck-együttható.
A jelenség jól használható hőmérsékletmérésre: ha az egyik érintkezési pont hőmérsékletét állandó értéken tartjuk (pl. olvadó jégben, vagy forrásban lévő cseppfolyós nitrogénben), akkor a Seebeck-együttható ismeretében a feszültség mérésével meghatározható a másik pont hőmérséklete.
Ha a kimenetet egy ellenállással terheljük, akkor az áramkörben áram fog folyni. Az érintkezési pontokon átfolyó áram egy másik termoelektromos jelenség, a Peltier-effektus következtében a meleg érintkezési pontot hűteni, a hideg pontot pedig melegíteni fogja. Az elnyelődő, illetve felszabaduló hőteljesítmény
áram fog folyni. Az érintkezési pontokon átfolyó áram egy másik termoelektromos jelenség, a Peltier-effektus következtében a meleg érintkezési pontot hűteni, a hideg pontot pedig melegíteni fogja. Az elnyelődő, illetve felszabaduló hőteljesítmény ![\[\frac{{\rm d}Q}{{\rm d}t}=\pi I=\alpha TI\]](/images/math/b/e/b/beb6bb50bc5cbb288095719722c19237.png)
ahol 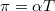 a az adott érintkezési pont abszolút hőmérsékletével arányos Peltier-együttható,
a az adott érintkezési pont abszolút hőmérsékletével arányos Peltier-együttható,  pedig a Seebeck-együttható.
pedig a Seebeck-együttható.
Ha ezeket a pontokat folyamatosan melegen ill. hidegen tartjuk, akkor egy közvetlenül elektromos energiát termelő hőerőgépet kapunk. A hatásfoka ugyan kicsi, de speciális körülmények között mégis célszerű a használata. Ilyen eszköz a radioizotópos termoelektromos generátor, ahol a meleg oldal fűtését az eszközben elhelyezett közepesen hosszú felezési idejű radioaktív izotópok bomlása biztosítja. Ezt az elektromos energiaforrást elsősorban olyan űreszközökben használják, amelyekben az energiaellátás napelemekkel nem megoldható (pl. a Naprendszer távoli részeiben).
Ha az eszközre külső feszültségforrásból kapcsolunk áramot, akkor hűtőgépként (hőszivattyúként) fog működni: a befektetett elektromos energia segítségével az egyik (hidegebb) érintkezési pontból hőt von el, a másikon pedig hőt szabadít fel. A gyakorlatban használt Peltier-elemekben különböző adalékolású (n- és p-típusú) félvezetőkből készülő termopárok vannak elektromosan sorba, míg hőtani szempontból párhuzamosan kapcsolva. Ha a fűtött oldalon felszabaduló hőt hűtőbordákkal, szellőztetéssel vagy vízhűtéssel elvezetjük, akkor a hűtött oldal a környezetnél jóval alacsonyabb hőmérsékletre hűthető. A hűtés hatékonyságát azonban a Peltier-elemben felszabaduló Joule-hő és a hővezetés is korlátozza.
Az eszközt széles körben használják számítógép alkatrészek és más elektromos berendezések hűtésére, valamint hordozható (kis egyenfeszültségről működtethető) hűtőgépekhez.
Az entrópia termodinamikai értelmezése, a II. főtétel megfogalmazása entrópiával
A belső energia egy (extenzív) állapotjelző, ezért két állapot közötti megváltozása független attól, hogy milyen folyamatokkal jutott a rendszer az egyik állapotból a másikba. A belső energia kétféleképpen változhat: hőközléssel és munkavégzéssel. A rendszer által felvett hő függ attól, hogy milyen folyamattal jutott a rendszer az egyik állapotból a másikba (épp ezt használják ki a ciklikus folyamatokkal működő gépek), ezért a felvett hő nem állapotjelző.
Clausius bevezetett egy olyan mennyiséget, az entrópiát, amely szoros kapcsolatban van a hőközléssel, de ugyanakkor állapotjelző. A klasszikus termodinamikában az entrópia megváltozása definiálható, reverzibilis (megfordítható) folyamatoknál :
entrópia megváltozása definiálható, reverzibilis (megfordítható) folyamatoknál : ![\[{\rm d}S=\frac{\delta Q}{T}\]](/images/math/9/d/1/9d1e57c107302781ad950770bfc3682b.png)
A kifejezésben  az abszolút hőmérséklet, az elemi hőközlésben használt
az abszolút hőmérséklet, az elemi hőközlésben használt 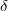 jel (a
jel (a 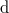 helyett) arra utal, hogy
helyett) arra utal, hogy  nem állapotjelző.
nem állapotjelző.
![\[\Delta S=\int_1^2{\rm d}S=\int_1^2\frac{\delta Q}{T}\]](/images/math/9/e/8/9e8df9ae0596605136de57257e4ddcb4.png)
A definíció csak az entrópia megváltozását határozza meg, egy egyelőre szabadon választott kezdőértékhez viszonyítva. (Az entrópia abszolút értékét a termodinamika III. főtétele segítségével lehet meghatározni.) Az entrópia mértékegysége J/K.
Irreverzibilis (nem megfordítható) folyamatokban az entrópia megváltozása![\[\Delta S\geq\int\frac{\delta Q}{T}\]](/images/math/a/f/e/afe62bddd91e3e694744fd42c1800cb6.png)
![\[Q=0\Rightarrow\Delta S\geq 0\]](/images/math/2/5/1/2514bf25d0145363ff99d1ebb78bc279.png)
Azaz zárt rendszer entrópiája nem csökkenhet. Ez a II. főtétel újabb megfogalmazása.
Ahogy láttuk, a tapasztalat szerint egy magára hagyott rendszerben a kezdeti hőmérséklet-, nyomás- és kémiai potenciál különbségek idővel kiegyenlítődnek. A kezdeti „rendezettség” (pl. forró és hideg víz, kis és nagy nyomás, szétválasztott komponensek) idővel irreverzibilisen (megfordíthatatlanul) a „rendezetlenség” (langyos víz, kiegyenlített nyomás, összekeveredett komponensek) irányába halad. Eközben viszont nő az entrópiája. Eszerint a (klasszikus termodinamikában szemléletes jelentés nélküli) entrópiát nevezhetjük a „rendezetlenség mértékének”.
Az entrópia statisztikus értelmezése alátámasztja ezt a megállapítást. A makroszkopikus állapotjelzők meghatározzák a rendszer egy makroállapotát. Ugyanakkor egy makroállapotot nagyon sok különböző mikroállapot valósíthat meg, ahol egy mikroállapot a rendszer részecskéinek egy adott konfigurációja a hely- és sebességkoordinátákból álló fázistérben. Feltesszük, hogy minden mikroállapot egyenlő valószínűséggel fordul elő. Ha egy makroállapotot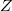 számú mikroállapot valósíthat meg, akkor a rendszer entrópiája
számú mikroállapot valósíthat meg, akkor a rendszer entrópiája ![\[S=k\ln Z\]](/images/math/4/1/d/41d931021bbcc7bc622e9e3e696c4c25.png)
ahol  a Boltzmann-állandó. (Egy adott makroállapothoz tartozó mikroállapotok leszámolása nem könnyű, és a klasszikus fizikában ellentmondásokra is juthatunk. A megoldást kvantumstatisztikák jelentik.) Kombinatorikai megfontolásokkal könnyen belátható, hogy „rendezetlen” makroállapotokat sokkal több mikroállapot valósít meg, és így a hozzá tartozó entrópia is nagyobb.
a Boltzmann-állandó. (Egy adott makroállapothoz tartozó mikroállapotok leszámolása nem könnyű, és a klasszikus fizikában ellentmondásokra is juthatunk. A megoldást kvantumstatisztikák jelentik.) Kombinatorikai megfontolásokkal könnyen belátható, hogy „rendezetlen” makroállapotokat sokkal több mikroállapot valósít meg, és így a hozzá tartozó entrópia is nagyobb.
Információ és entrópia
A Maxwell-démon és néhány híres feloldási kísérlete
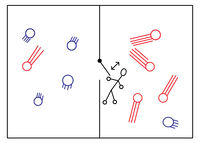
A Maxwell-démon egy híres gondolatkísérlet szereplője. A Maxwell által felvetett gondolatkísérletben egy gáztartályt hőszigetelő fallal kettéosztunk, amin egy kicsiny nyitható-csukható ajtó van. Egy apró lény (ő a „démon”) az ajtót attól függően nyitja vagy csukja, hogy melyik irányból milyen sebességű molekula érkezik. Ha az átlagosnál gyorsabb molekulákat pl. csak balról jobbra engedi át, akkor az eredetileg azonos hőmérsékletű két fél közül a jobboldali – külső hatás nélkül – felmelegszik, míg a baloldali lehűl. Ezzel egy zárt rendszer entrópiája csökkenne, ami viszont ellentmond a termodinamika II. főtételének.
A paradoxon feloldására sok kísérlet született, az egyik Szilárd Leó gondolatmenete. Egy „valódi” démonnak valahogy meg kell mérnie a molekulák sebességét (a méréshez például egy apró zseblámpával meg kell világítania a molekulákat). Ehhez a démonnak energiát kell felhasználnia, ami viszont megnöveli az entrópiáját. A démon entrópianövekedése nagyobb, mint a gáz entrópiacsökkenése, így az egész rendszer (gáz + démon) entrópiája nem fog csökkenni.
Landauer ellenvetése szerint viszont a mérési folyamatnak nem feltétlenül kell növelnie a rendszer entrópiáját, ha a folyamat reverzibilis (megfordítható). A reverzibilitáshoz viszont a démonnak minden mérési adatot fel kell jegyeznie, és meg kell őriznie. A memóriakapacitása nem lehet végtelen, ezért előbb-utóbb törölnie kell a régebbi mérési adatokat, ami viszont a mérést irreverzibilissé (meg nem fordíthatóvá) teszi. Az irreverzibilis folyamat viszont entrópianövekedéssel jár, tehát az információ törlése növeli a rendszer entrópiáját. 1 bit információ törlése![\[\Delta S\geq k\ln 2\]](/images/math/c/a/b/cabab03fb0b96eab48f82032b0a0efcb.png)
![\[Q\geq kT\ln 2\]](/images/math/4/6/3/463cb55256369dd2751f26e4deab29fd.png)
A Maxwell-démontól így eljutottunk az információs entrópia fogalmához. Az információelméletben az entrópia egy üzenet bizonytalanságát, azaz várható információtartalmát méri. Egy előre ismert, pl. csupa azonos karakterből álló üzenet bizonytalansága – és így információtartalma nulla. Egy véletlenszerű karaktersorozatnak viszont maximális az információtartalma, és így az entrópiája is.
A zaj
A zaj jellemzése, néhány oka
A zaj a mért jelre, továbbított információtartalomra különböző okokból „rárakódó” zavar. A zaj eredetileg az akusztikában használt fogalom, de általánosabb értelemben bármely (elektromos, optikai, stb.) analóg vagy digitális jelnél fellépő véletlenszerű ingadozás zaj.
Analóg jeleknél a zaj a spektrumával jellemezhető. A fehérzajban a jel intenzitása a vizsgált tartományban minden frekvencián egyforma, az 1/f zaj spektrális intenzitása pedig fordítva arányos a frekvenciával.
A zajnak nagyon sok oka lehet. Az elektromos jelekben mindig fellépő termikus zaj a töltéshordozók hőmozgásából adódik. A p-n átmenetekben fellépő sörétzajt pedig az elektromos töltés kvantáltsága okozza: az átmeneten időegységenként átlépő töltéshordozók száma fluktuál.
Az információ kinyerése erősen zajos jelekből: a Hold-radar kísérlet
A II. világháborúban új technika született: a radar. A háború alatt az Egyesült Izzóban is folytak radarfejlesztések. A háború végén felmerült a lehetősége, hogy a földi tárgyakról visszaverődő radarjelekhez hasonlóan a Holdról visszaverődő jeleket is detektálni lehet. A fő nehézséget az okozza, hogy a Hold nagy távolsága miatt a visszaverődő jel sok nagyságrenddel gyengébb, és így a jel-zaj viszony is sokkal kisebb, mint a földi célpontok esetében.
A berendezések tökéletesítésével, 0,05 s hosszú impulzusokkal és 20 Hz sávszélességű vevővel a jel-zaj viszonyt a kor technikájával legfeljebb 1/10-re lehetett javítani – ez azt jelenti, hogy a jelek még mindig egy nagyságrenddel kisebbek a zajnál. A megoldást az jelentette, hogy a kibocsátott jeleket periodikusan ismételték, és a beérkező jeleket összegezték. A zaj az összegzés során részben kiátlagolódik, a jel viszont folyamatosan növekszik, így kellően hosszú összegzés után a jel érzékelhetően a zaj fölé nő.
A méréstechnikában ma már széles körben használt lock-in erősítők ugyanezen elven alapulnak, de akkoriban még sokkal nehezebb volt ötlet gyakorlati megvalósítása. A jel N impulzus összegzésekor  -szeresére nő, a zaj viszont csak
-szeresére nő, a zaj viszont csak 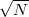 -szeresére, így a jel-zaj viszony is
-szeresére, így a jel-zaj viszony is 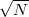 -szeresére javul. A Holdról kb. 2,5 másodperc alatt érkeznek vissza a radarhullámok, így 3 másodpercenként lehetett a jeleket kibocsátani. 1000 impulzus kibocsátása (a jel-zaj viszony kb. 30-szoros javítása) 50 percig tart. Akkoriban nem volt olyan elektromos eszköz, amivel a jeleket ilyen hosszú ideig lehetett összegezni.
-szeresére javul. A Holdról kb. 2,5 másodperc alatt érkeznek vissza a radarhullámok, így 3 másodpercenként lehetett a jeleket kibocsátani. 1000 impulzus kibocsátása (a jel-zaj viszony kb. 30-szoros javítása) 50 percig tart. Akkoriban nem volt olyan elektromos eszköz, amivel a jeleket ilyen hosszú ideig lehetett összegezni.
Összegzésre az elektrolízist használták: az elbontott víz mennyisége – amit egy vékony csőben a folyadékszint eltolódásából lehetett leolvasni – arányos az áram integráljával. A vevő felerősített jelét 0,3 másodperces késleltetéssel 10 egymás utáni csövecskéhez kapcsolták. Ugyanez a mechanikus kapcsoló indította 3 másodpercenként a kibocsátott jeleket is, így az egyes csövecskékhez meghatározott időkésleltetés kapcsolódott. A Holdról visszaverődött jel így mindig ugyanabban a csövecskében bontotta a vizet, a többi csőben fejlődő gáz viszont csak a zajt mérte.
Előzetes számítások és a háborús viszontagságok után Bay Zoltán vezetésével 1945 nyarán kezdték építeni azt a berendezést, amellyel végül 1946. február 6-án – a sokkal jobb eszközökkel dolgozó amerikaiak után néhány héttel, a világon másodikként – sikerült detektálni a Holdról visszaverődő radarjeleket: a megfelelő csövecskében a folyadékszint egyértelműen a többi fölé emelkedett.
A kísérletből kiderült, hogy a radar 2,5 m hullámhosszú jele átjut a légkörön, és kijut a világűrbe, a Hold visszaverőképessége pedig kb. 1/10 ezen a hullámhosszon. A kísérlet a világűrkutatás új, „aktív” korszakát nyitotta meg.
Zaj és önszerveződés
Szegregáció és mintázatképződés granulált anyagoknál
A granulált anyagok különböző alakú és méretű szemcsékből állnak. A szemcsék nagysága a mikrométeres mérettől (pl. festékporok) a több méteresig (pl. sziklagörgetegek) terjedhet. Alakja lehet sima felületű gömb vagy szögletes, szabálytalan formájú szemcse. Tipikus, jól ismert, és gyakran vizsgált granulált anyag a homok.
A granulált anyagok viselkedése sok furcsaságot mutat. Folyadékokhoz hasonlóan önthetők, de ugyanakkor a kiöntött anyag nem terül szét teljesen, hanem egy anyagra jellemző rézsűszögű kupacot alkot. Még különösebben viselkednek a granulált anyagok keverékei: rázás, mozgatás, kiöntés hatására a várakozásokkal ellentétben nem összekeverednek, hanem szétválnak. Ez a spontán szegregáció jelensége. Az 5. ábrán párhuzamos falak közé öntött mák-homok keverék látható. Az egyes rétegek véletlenszerű fluktuációk hatására meginduló kis lavinák hatására alakulnak ki.
Egy másik meglepő jelenség a granulált anyagok rázásakor megfigyelhető mintázatképződés. Ha egy hengeres edénybe öntött vékony réteg homokot, vagy más granulált anyagot függőleges irányban rázni kezdünk, akkor az edény 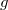 -nél nagyobb maximális gyorsulása esetén a szemcsék ugrálni kezdenek, az ugráló részecskék pedig egymással és az edény aljával ütköznek. Azt várnánk, hogy a sok véletlenszerű ütközésből egy teljesen rendezetlen mozgás alakul ki, azonban az anyag különböző – a frekvenciától és a maximális gyorsulástól függő – mintázatokat alakít ki. A 6. ábrán három különböző mintázat látható, melyek 0,15 mm átmérőjű üveggyöngyök rázásakor alakultak ki. Bizonyos körülmények között a rezgetett rétegben hosszabb ideig stabil, lokalizált hullámok un. oszcillonok is kialakulhatnak.
-nél nagyobb maximális gyorsulása esetén a szemcsék ugrálni kezdenek, az ugráló részecskék pedig egymással és az edény aljával ütköznek. Azt várnánk, hogy a sok véletlenszerű ütközésből egy teljesen rendezetlen mozgás alakul ki, azonban az anyag különböző – a frekvenciától és a maximális gyorsulástól függő – mintázatokat alakít ki. A 6. ábrán három különböző mintázat látható, melyek 0,15 mm átmérőjű üveggyöngyök rázásakor alakultak ki. Bizonyos körülmények között a rezgetett rétegben hosszabb ideig stabil, lokalizált hullámok un. oszcillonok is kialakulhatnak.
Fraktálok
A kristályok növekedése a magképződéssel (nukleáció) kezdődik, majd ezt követi a kristályszemcse növekedése. A növekedési sebességet a lokális hőmérséklet és koncentráció befolyásolja, amelyekre viszont visszahat a kristályosodás. Emiatt a kristály növekedési sebessége erősen helyfüggő lesz, és a véletlen fluktuációk (zajok) hatására kialakuló kis „dudorok” sokkal gyorsabban nőnek. Ezeken a gyorsan növő részeken újabb véletlen fluktuációk hatására elágazások alakulnak ki, amely végül egy faágakra emlékeztető kristály kialakulásához vezet. A jelenség hókristályok és a zúzmara kialakulásakor is megfigyelhető.
A kialakuló forma fraktálos szerkezetet mutat: azaz a kristály egyre kisebb méretekben ismétlődő önhasonló formákból épül fel.
Kollektív mozgások, közlekedési dugók
Izgalmas határtudomány a madár- és halrajok vagy tömegből menekülő emberek kollektív mozgásának vizsgálata. A számítógépes modellek szerint ezek a látszólag nagyon bonyolult mozgások három egyszerű elv hatására alakulnak ki: minden egyed lehetőleg ugyanarra akar haladni, mint a szomszédai; mindegyik a szomszédai közelében akar maradni; de az összeütközést el akarja kerülni.
A kicsiny fluktuációk felerősödése jól megfigyelhető a közlekedésben is: az autópályákon kialakuló közlekedési dugókban gyakran megfigyelhető, hogy az autóoszlop többé-kevésbé periodikusan teljesen megáll, majd aránylag gyorsan mozog. A teljesen telített úton egyetlen véletlen fékezés is fékezések egész sorát okozhatja, amitől akár teljesen leáll a forgalom. Az így lelassuló autók előtt viszont üres útszakasz alakul ki, tehát a meginduló autók hirtelen sokkal gyorsabban haladhatnak – egészen addig, amíg utol nem érik a lassabb kocsioszlopot. Ez újabb fékezésekhez, és a folyamat ismétlődéséhez vezethet.
Vissza a Fizika 1i nyitóoldalára
1. Tér és idő
3. Megmaradási törvények a mechanikában
4. Rezgések
5. Rend és rendetlenség
6. Hideg-meleg