„Piezoelektromos állandók mérése” változatai közötti eltérés

A lap 2013. augusztus 3., 19:32-kori változata (lapforrás) LaszloV (vitalap | szerkesztései) ← Régebbi szerkesztés		A lap 2013. augusztus 4., 08:23-kori változata (lapforrás) LaszloV (vitalap | szerkesztései) Újabb szerkesztés →
210. sor:		210. sor:
	===Mérés a direkt piezoelektromos effektus alapján===		===Mérés a direkt piezoelektromos effektus alapján===
		+
		+	Ez a piezoelektromos állandók meghatározásának talán legkorábban alkalmazott módszere. A mérés eredeti változatánál a megfelelő elektródokkal ellátott vizsgálandó mintára meghatározott súlyú testet helyeztek (vagy emeltek le) és közben megmérték a töltés mennyiség megváltozását az elektródokon. Ennek az eljárásnak legfőbb hibaforrásai egyrészt az erőátadás bizonytalanságából, másrészt a töltésmennyiség mérésének nehézségéből adódnak. Sokkal megbízhatóbb a mérés, ha a vizsgálandó mintát periodikusan változó erőhatásnak tesszük ki. Az általunk alkalmazott mérés során periodikus terhelést alkalmazunk.
		+
		+	A vizsgálandó piezoelektromos kerámia esetén a mérés alapját a LINK (18) egyenletek képezik. Ezzel a módszerrel a $d_{33}$  együtthatót fogjuk meghatározni, vagyis a LINK (18) egyenletek közül az utolsót kell alkalmaznunk. Ennek megfelelően a mintát úgy kell kialakítani, hogy a nyomóerőt a 3 irányban lehessen működtetni ($T_{33}$), és a keletkező töltést a 3 irányra merőleges lapokon lehessen megmérni (ilyent okoz a $P_3$ megváltozása). Ezt a LINK 2. ábrán látható módon elkészített minta segítségével érhetjük el. Ekkor a mechanikai feszültség és a létrejött polarizáció között az alábbi összefüggés áll fenn:
		+
		+	{{eq| P_3 {{=}} d_{33}T |eq:20| (20) }}
		+
		+	2. ÁBRA
		+
		+	Feltételezve, hogy a mérés során a töltésveszteség (pl. átvezetés miatt) elhanyagolható, a piezoelektromos polarizáció ($P_3$) a mintán megjelenő feszültség mérésével határozható meg:
		+
		+	{{eq| P_3 {{=}} \sigma {{=}} \frac{Q_p}{A_p} {{=}} \frac{CU_p}{A_p}  |eq:21| (21) }}
		+
		+	ahol ($U_p$)  az elektródokon a polarizáció változása által okozott feszültség, $C$ a minta kapacitásának és a feszültségmérő bemenetén levő kapacitásnak az eredője, $A_p$ pedig a piezoelektromos mintán elhelyezett elektródok felülete.
		+	A mintában létrejött feszültséget ($T_{33}$) egy, az általa egy mérőrugóban létrehozott alakváltozásból határozzuk meg (l. alább).
		+
		+	====A mérőberendezés használata====
		+
		+	A mérésnél alkalmazott berendezés blokkvázlatát a LINK 3. ábrán mutatjuk be. A vizsgálandó piezokerámia lapot nyomótalpak közé helyezzük. A nyomótalpak felületei a testtől elszigetelt elektródokká vannak kiképezve, így a mérés során megjelenő töltések a mérőkondenzátorba töltődnek. A mintát terhelő periodikus erőhatást a szolenoid változó mágneses tere által rezgésbe hozott vasmag hozza létre. Az erő mértékének meghatározására a mérőrugó szerepét betöltő konzol deformációját használjuk. A deformációt nyúlásmérő bélyegekkel mérjük.
		+	A mérés elvégzéséhez az erőmérőt és a töltésmérő eszközt hitelesíteni kell, amit az alábbi módon végezhetünk el.
		+
		+	====Az erőmérő hitelesítése és a nyomófeszültség mérése====
		+
		+	Bár a mérés során periodikus erőhatást alkalmazunk, az erőmérő hitelesítését elegendő statikus módszerrel (súlyok felhelyezésével) elvégezni. Ehhez a mérőhíd kimenetére kapcsoljunk digitális multimétert. A mérés megkezdése előtt a nyúlásmérő bélyeg mérőhídját a minta terheletlen állapotában egyenlítsük ki. Ezután zárjuk össze a nyomótalpakat (akár úgy, hogy a piezokerámia már közte van), és a megbízható erőhatás érdekében a beállító csavarral kb.  10 N erővel feszítsük elő a rendszert, és olvassuk le a kimenőfeszültség értékét. Ezután megkezdhetjük a hitelesítést  úgy, hogy különböző súlyokat helyezünk el a szolenoid lengő vasmagjához rögzített – erre a célra kiképezett – felületre, és leolvassuk a mérőhíd kimenetén megjelenő feszültséget. A kimenőfeszültséget ( $U_{ki}$ ) ábrázolva az alkalmazott súly által kifejtett erő függvényében, jó közelítéssel lineáris összefüggést kapunk, és meghatározzuk a pontokhoz illesztett egyenes meredekségét:
		+
		+	{{eq| k {{=}} \frac{ \Delta F}{ \Delta U_{ki} } |eq:22| (22) }}
		+
		+	Ezzel a mért feszültségből a mintára ható $F$ erőt az
		+
		+	{{eq| F {{=}} F_0 +k \left( U_{ki} - U_0 \right) |eq:23|  (23) }}
		+
		+	összefüggésből számíthatjuk ki ( $F_0$ az előfeszítést adó erő, $U_0$ pedig az ehhez tartozó kimenőfeszültség). A LINK (20) egyenletben szereplő mechanikai feszültséget a
		+
		+	{{eq| T_{33} {{=}} \frac{F}{A_p} |eq:24|  (24) }}
		+
		+	egyenlet adja meg.
		+
		+	====A töltés hitelesítése és a piezoelektromos polarizáció meghatározása====
		+
		+	A piezokerámia anyagok általában jelentős relatív permittivitással rendelkező dielektrikumok, így ha egy mintán elektródokat alakítunk ki, számottevő kapacitású piezoelektromos „kondenzátor” jön létre. Elvileg a mechanikai feszültség által létrehozott töltést ezen a „kondenzátoron” is megmérhetnénk, ez a kapacitás azonban általában erősen függ a hőmérséklettől, sőt az alkalmazott feszültségtől is, így a töltést célszerű – a 4. ábrán látható módon – a piezokerámia $C_0$ kapacitásánál lényegesen nagyobb $C_1$  mérőkapacitáson fellépő feszültség alapján meghatározni.
		+
		+	4.  ÁBRA
		+
		+	A mért $U-p$  feszültségből ekkor a piezoelektromos polarizáció a LINK (21) egyenlet alapján számítható ki
		+
		+	{{eq| P_3 {{=}} \frac{CU_p}{A_p}  |eq:25|  (25) }}
		+
		+	ahol $A_p$ a mintán elhelyezett elektródok felülete, és $C = C_0 + C_1$ . A $C_1$ mérőkapacitás vagy ismert (gyári adat) vagy értékét méréssel határozzuk meg. A $C_0$ kapacitás értékét vagy megmérjük, vagy – ha a minta anyagának permittivitását ismerjük – a síkkondenzátor kapacitására vonatkozó ismert összefüggés segítségével kiszámítjuk.
		+
		+	====Mérés periodikus mechanikai feszültség alkalmazásával====
		+
		+	A periodikus erő nagyságának változtatása a LINK 3. ábrán vázolt szolenoidra kapcsolt jel amplitúdójának változtatásával történik, és ekkor a nyúlásmérő híd kimenetén váltófeszültség jelenik meg. A polarizáció meghatározására szolgáló mérőkondenzátoron ekkor ugyancsak váltófeszültséget mérünk. A $d_{33}$ piezomodulus a mért $U_p$ és $U_{ki}$ feszültségekből a LINK (20), (23), (24) és (25) egyenletek segítségével kapható meg:
		+
		+	{{eq| d_{33} {{=}} \frac{CU_p}{F_0+k \left( U_{ki} - U_0 \right) }    |eq:26| (26) }}
		+
		+	====Mérési feladatok====
		+
		+	* LINK 2.1.5.1 Végezze el a mérőrendszer hitelesítését.
		+	* LINK 2.1.5.2 Határozza meg a kerámia minta  piezomodulus értékét két különböző terhelőerő alkalmazásával.
		+
		+
		+	===Piezoelektromos állandók mérése az inverz piezoelektromos effektus alapján statikus módszerrel===
		+
		+	Az inverz effektus alapján történő mérés egyik lehetséges módja az, hogy a piezoelektromos mintára időben állandó elektromos feszültséget kapcsolunk, és megmérjük a létrejött deformációt. Ez a mérési eljárás a piezomodulusok meghatározására a LINK (19) egyenletek alapján ad módot. Mérésünk során a $d_{31}$ állandót fogjuk meghatározni, ezért a LINK (19) egyenletek közül a legelsőt,
		+
		+	{{eq| S_1 {{=}} d_{31}E_3 |eq:27| (27) }}
		+
		+	használjuk.
		+	A mintát most úgy kell kialakítanunk, hogy ''3'' irányú elektromos teret alkalmazhassunk (az elektródok a ''3'' irányra merőlegesek legyenek), és mérni tudjuk az ''1'' irányú megnyúlást (összehúzódást). Mivel a mintában létrejövő térerősség adott elektromos feszültség esetén annál nagyobb, minél vékonyabba minta, a létrejött deformáció pedig arányos a mintának a deformáció irányába eső hosszával, mintaként célszerű a ''3'' irányban vékony, az ''1'' irányban pedig hosszú lemezt alkalmazni LINK (5. ábra).
		+
		+	5. ÁBRA
		+
		+
		+
		+
		+

---

A lap 2013. augusztus 4., 08:23-kori változata

szerkeszt/-va/-ve/-ván/-vén alatt

A mérés célja:

• megismertetni a hallgatókat a piezoelektromos effektusokkal, a piezoelektromos állandók értelmezésével, illetve azok kísérleti meghatározási módszereivel.

A cél érdekében:

• értelmezzük a piezoelektromos állandókat,
• ismertetjük a kísérleti meghatározás lehetőségeit,
• ismertetjük a mérés során alkalmazott vizsgálati módszereket, a mérőkészülék felépítését és működését,
• megmérjük kerámia minták piezoelektromos állandóit.

Tartalomjegyzék 1 Elméleti összefoglaló 2 A piezoelektromos állandók meghatározása 2.1 Mérés a direkt piezoelektromos effektus alapján 2.1.1 A mérőberendezés használata 2.1.2 Az erőmérő hitelesítése és a nyomófeszültség mérése 2.1.3 A töltés hitelesítése és a piezoelektromos polarizáció meghatározása 2.1.4 Mérés periodikus mechanikai feszültség alkalmazásával 2.1.5 Mérési feladatok 2.2 Piezoelektromos állandók mérése az inverz piezoelektromos effektus alapján statikus módszerrel

Elméleti összefoglaló

Ha egy anyagot valamilyen külső hatás ér, akkor abban különböző változások jönnek létre, az anyag valamilyen módon „reagál” a külső hatásokra, amit megfigyelőként a hatástól függő jelenségként észlelünk. Mind az anyagot ért hatások, mind pedig az anyagban ilyenkor észlelhető jelenségek fizikai szempontból valamilyen fizikai mennyiséggel – illetve annak megváltozásával – jellemezhetők. Az, hogy meghatározott körülmények között egy hatás milyen erősségű változást (jelenséget) hoz létre, függ a vizsgált anyagtól, pontosabban az anyagnak az adott jelenség szempontjából fontos tulajdonságától.

Például: ha egy anyagot melegítünk, akkor az anyagot ért hatás a hőmérséklet változásával jellemezhető, a hőmérsékletváltozás által kiváltott egyik lehetséges jelenség pedig az, hogy megváltozik az anyag térfogata. Ugyanolyan hőmérsékletváltozás azonban különböző anyagokban különböző térfogatváltozást okoz, vagyis a jelenség „mértéke” az anyagi minőségtől függ és az anyag egy tulajdonságával – a térfogati hőtágulási együtthatóval – jellemezhető. Egy másikismert példa, hogy egy szigetelőanyag elektromos tér hatására polarizálódik. Itt a hatás az elektromos térerősség-vektorral, a jelenség a polarizáció-vertorral, a jelenségnek az anyagi minőségtől való függése pedig egy tenzorral, a dielektromos szuszceptibilitás tenzorával jellemezhető. Hasonlóan: egy test erőhatás következtében létrejövő alakváltozása esetén a hatás a feszültségtenzorral, a jelenség az alakváltozási tenzorral, az anyag tulajdonságai pedig a rugalmas együtthatókkal (amelyek ugyancsak tenzort alkotnak) jellemezhető.

A jelenségek számszerű leírásának alapvető feltétele az, hogy a vizsgált esetre vonatkozóan ismerjük a hatást, a jelenséget és a tulajdonságot jellemző fizikai mennyiségek közötti összefüggést. Szerencsére számos olyan jelenséget ismerünk amelynél – nem túl nagy hatások esetén – ez az összefüggés igen egyszerű formában írható fel. A pontos megfogalmazást egyelőre mellőzve, azt mondhatjuk, hogy a hatást és a jelenséget jellemző mennyiségek között egyfajta lineáris összefüggés áll fenn, amely szimbolikusan az alábbi alakban írhatunk fel:

Itt a „jelenség”, „tulajdonság”, „hatás” elnevezés fizikai mennyiségeket jelöl, amelyek matematikai szempontból skaláris- vektor- vagy tenzormennyiségek lehetnek. Ennek megfelelően a „ ” jel is különböző műveleteket jelenthet. Az említet példák közül az állandó nyomás (P) mellett végbemenő hőtágulás esetében a hatás a 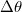hőmérsékletváltozás, a jelenség a 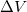térfogatváltozás, a tulajdonság pedig az 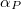térfogati hőtágulási együttható. Az említett mennyiségek között az egyszerű

tapasztalati összefüggés áll fenn (itt mindhárom mennyiség skalár). A másik példában a hatást jellemző E térerősség-vektor és a jelenséget jellemző P polarizáció-vektor kapcsolata – a vektorok derékszögű koordinátarendszerbeli komponenseit 1, 2, 3-mal jelölve – az alábbi lineáris egyenletekkel adható meg

Az egyenletben szereplő 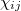mennyiségek egy másodrendű tenzor komponensei, amelyet a

szimbólummal jelölhetünk. Ezzel a jelöléssel a LINK (3) egyenleteket sűrített formában gyakran az alábbi módón írják fel:

Ez az írásmód egy ilyen – másodrendű tenzort – tartalmazó egyenletnél még egyértelmű, magasabb rendű tenzorok esetén azonban nem derül ki belőle a szereplő tenzorok rendje, ezért helyette rendszerint az egyenleteket – bizonyos megállapodásokkal – rövidített indexes alakban használják. A LINK (3) egyenlet ilyen indexes alakja:

azzal a megállapodással, hogy az egyenletben ugyanazon tagban előforduló, megegyező indexekre (a LINK (6) egyenletben tehát j-re) összegezni kell, a magában álló index (i) helyébe pedig az 1, 2, vagy 3 érték helyettesítendő be ( így kapunk 3 egyenletet). Ugyanilyen alakban írható fel a másodrendű tenzorral jellemezhető mechanikai feszültség (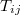) és a deformáció (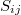) közötti kapcsolatot megadó általános Hooke-törvény is:

ahol a 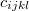mennyiségek egy negyedrendű tenzor komponensei, amelyeket rugalmas állandóknak neveznek. Ugyanez a törvény úgy is felírható, hogy a deformációkat fejezzük ki a feszültségekkel, azaz

Az itt szereplő mennyiségek szintén egy negyedrendű tenzort alkotnak, amelyeket merevségi együtthatóknak neveznek.

Mivel gyakran előfordul, hogy ugyanazt a jelenséget többféle hatás is létrehozhatja, fontos megadni, hogy a jelenség milyen feltételek között ment végbe. Ennek megfelelően a fenti egyenletek csak akkor érvényesek, ha a jelenséget a vizsgált esetekben csak az egyenletekben szereplő egyetlen hatás váltja ki. A továbbiakban vizsgálandó jelenségek éppen azzal kapcsolatosak, hogy bizonyos anyagokban elektromos polarizációt nem csak az elektromos tér, hanem más hatások is létrehozhatnak, illetve hogy egy anyag deformációja nem csak mechanikai feszültség, hanem más hatások eredménye is lehet, és ilyenkor a LINK (6) és a (8) egyenletet módosítani kell.

A tapasztalat azt mutatja, hogy polarizáció-változást – az elektromos tér mellett - létrehozhat hőmérsékletváltozás és mechanikai feszültség is. Azt a jelenséget, melynek során egy anyag polarizációja megváltozik, piroelektromos effektusnak nevezik. A hőmérsékletváltozás (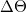) által létrehozott polarizáció a már említett lineáris séma szerint fejezhető ki a hőmérsékletváltozással:

ahol a 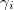mennyiségek a piroelektromos együtthatók, amelyek egy vektor (elsőrendű tenzor) komponensei. Bizonyos anyagokban polarizáció-változást mechanikai feszültség is eredményezhet. Ezt a jelenséget piezoelektromos effektusnak nevezik, és a mechanikai feszültség által létrehozott polarizációra szintén a fentiekhez hasonló lineáris törvény érvényes:

A 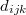mennyiségek egy harmadrendű tenzort alkotnak, amelyeket piezoelektromos modulusoknak neveznek. A piezoelektromos effektust mutatóanyagok a piezoelektromos anyagok.

Az elektromos tér, hőmérsékletváltozás és mechanikai feszültség együttes hatása miatt létrejött polarizációt a szuperpozíció elvének alkalmazásával a LINK (6), (9), és (10) egyenletekből kapjuk meg:

A három effektus közül a továbbiakban a piezoelektromos effektussal foglalkozunk, és feltételezzük, hogy a másik két hatás által okozott polarizáció elhanyagolható, vagyis a LINK (11) általános egyenlet helyett a LINK (10) egyenlet használható.

Tapasztalatból tudjuk, hogy egy test deformációja nem csak mechanikai feszültség, hanem hőmérsékletváltozás és – bizonyos anyagokban – elektromos tér hatására is létrejöhet. A hőtágulás jelensége eléggé ismert, anizotróp anyagokban azonban a hőtágulás is irányfüggő lehet, így a jelenséget leíró egyenlet az alábbi alakban írható fel:

Az 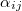konstansok hőtágulási együtthatók, amelyek egy másodrendű tenzort alkotnak. Piezoelektromos anyagokban deformáció létrejöhet elektromos tér hatására is. Ez a jelenség az inverz piezoelektromos effektus, amelynek leírása a szokásos lineáris egyenletekkel történik:

Ebben az egyenletben ugyanazok az állandók szerepelnek, mint a piezoelektromos effektust leíró LINK (10) egyenletben. A három hatás együttes eredményeként létrejött deformációt az alábbi összefüggés adja meg

A továbbiakban ezek közül a jelenségek közül csak az inverz piezoelektromos effektussal foglalkozunk, és feltételezzük, hogy a deformáció egyedüli oka az elektromos tér, vagyis használhatjuk a speciális estre vonatkozó LINK (13) összefüggést.

A piezoelektromos effektusok (piezoelektromos- és inverz piezoelektromos effektus) gyakorlati felhasználása azon alapul, hogy egy test felületén külső mechanikai hatás következményeként megváltozik az elektromos töltéseloszlás, illetve a külső elektromos tér a testet deformálja. A gyakorlatban az ilyen anyagok egyre nagyobb szerepet kapnak, mint erő- és elmozdulás érzékelők, rezgéskeltők, nagypontosságú mechanikai helyzetbeállítók, stb.

A kristályos anyagok jelentős része mutat piezoelektromos tulajdonságokat, gyakorlati alkalmazhatóságuk e jelenség mértékétől függ, ami számszerűen a piezomodulusokkal jellemezhető. A 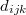piezoelektromos modulus-tenzornak 27 eleme van, de szerencsére egy anyag – még a legáltalánosabb esetben is – ennél jóval kevesebb számú piezomodulussal jellemezhető. Tudjuk, hogy a 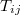feszültségtenzor és az 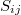alakváltozási tenzor szimmetrikus, azaz érvényes a 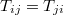és az 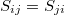összefüggés. Ez azt jelenti, hogy a test egy pontjában a feszültség és az alakváltozás jellemzésére csak 6-6 mennyiségre van szükség, ezért bevezették a következő indexelési konvenciót: a főátló elemei rendre 1, 2, 3, míg az azon kívüli elemek, tehát a vegyes indexű tagok a 4, 5, 6, indexeket kapják. Ezáltal a két tenzor az alábbi, 6-6 különböző elemet tartalmazó két mátrix formájában írható fel:

A mátrixokból az átindexelés pontos sémája leolvasható. Kimutatható, hogy a fenti két tenzor szimmetrikus volta miatt a piezomodulus-tenzor elemeire is fennáll egyfajta szimmetria (a második és harmadik indexek felcserélhetők):

aminek alapján az elemek száma itt is csökkenthető. A tenzorkomponensek második és harmadik indexeire alkalmazva a feszültség- és alakváltozási tenzornál megismert átindexelést (11→1, 22→2, 33→3, 23→4, 13→5, 12→6), a 27 elemet tartalmazó harmadrendű kétindexes mátrix formájába írható át:

A fenti mátrixok segítségével a piezoelektromos effektust leíró egyenletek az eredeti LINK (10) egyenleteknél egyszerűbb

alakba írhatók. Hasonló módon egyszerűsíthetők az inverz piezoelektromos effektus LINK (13) egyenletei is:

A LINK (16) és (17) egyenletek tovább egyszerűsödnek a vizsgált anyag kristálytani szimmetriái következtében. A kristály szimmetriáitól függően ugyanis a 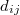mátrix egyes elemei nullává válhatnak, illetve bizonyos elemek egymással megegyezhetnek, ami tovább csökkenti az anyag piezoelektromos tulajdonságainak jellemzéséhez szükséges független állandók és az egyenletekben fellépő tagok (esetleg az egyenletek) számát.

A mai gyakorlatban a kristályos piezoelektromos anyagok közül leggyakrabban a kvarccal találkozunk (kvarcórák rezonátora), de a legnagyobb mennyiségben alkalmazott piezoelektromos anyagok az ólom-cirkonát-titanát (PZT) alapú kerámiák, amelyek bizonyos területeken az olcsóbb, tömeggyártásra alkalmas technológiájuknak köszönhetően, az egykristályokat szinte teljesen kiszorították. A piezokerámiák polikristályos anyagok, így szerkezetükben a krisztallitok rendezetlen irányítottsággal helyezkednek el. A gyártás során a kerámiai anyagot polarizálják, más szóval maradandó elektromos anizotrópiát alakítanak ki a szerkezetében. A polarizálás megfelelően nagy (az átütési szilárdságot megközelítő) elektromos térrel történik, aminek hatására a véletlenszerűen elhelyezkedő kristályszemcsék polarizációvektorai többé-kevésbé rendeződnek, és így az anyagban makroszkopikus elektromos polarizáció alakul ki. Ha a 3 tengely a polarizáció irányába mutat, akkor egy ilyen polarizált kerámiában a piezoelektromos modulus egyszerűsített mátrixa a következőképpen alakul:

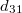A és 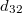, valamint a 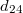és 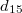elemek értékei egymással megegyeznek, ezért a kerámia piezoelektromos szempontból a 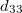, , 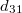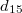három független állandóval jellemezhető. A piezoelektromos effektust leíró egyenletek ebben az esetben tehát így alakulnak:

Az első egyenlet a 3 irányra merőleges síkban működő irányú nyírófeszültség (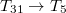 ) által az 1 irányban-, a második egyenlet a 3 irányra merőleges síkban működő irányú nyírófeszültség ( 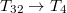) által a 2 irányban-, a harmadik egyenlet pedig a három tengely irányában ható normális feszültségek ( 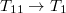, , 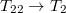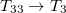) által a 3 irányban létrehozott polarizációt adja meg. A fentiekből látható, hogy a piezomodulus-mátrix elemeinek első indexe mindig az elektromos tér, a második pedig a mechanikai hatás irányát mutatja meg. A feszültségek és a létrehozott polarizáció közötti kapcsolatot az LINK 1. ábrán mutatjuk be.

1. ÁBRA

Hasonló módon kaphatók meg az inverz piezoelektromos effektus egyenletei, amelyek ebben az esetben az alábbi alakot öltik:

Mint látható, itt a piezomodulus-mátrix elemeiben az első index a térerősség-, a második pedig a deformáció irányát mutatja meg. A 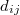állandók egysége C/N vagy az ezzel egyenértékű m/V, ami szemléletesen fejezi ki, hogy hány coulomb töltés jelenik meg 1N terhelőerő esetén egy hasáb alakú piezoelektromos test két szemben lévő felületén elhelyezett elektródokon, illetve az inverz piezoelektromos effektust kihasználva, mekkora deformációt szenved a test, ha az elektródokra 1V feszültséget kapcsolunk. Megjegyzendő, hogy a piezoelektromos anyagok egy részénél a fenti egyenletek nagy térerősségeknél nem használhatók, mert ilyenkor a polarizáció - mechanikai feszültség, illetve a deformáció – elektromos térerősség összefüggés nem lineáris, és a permittivitás függ a térerősségtől.

A piezoelektromos állandók meghatározása

A piezoelektromos állandók mind a direkt, mind pedig az inverz piezoelektromos effektus alapján meghatározhatók. A méréseket rendszerint hasáb alakú mintákon végzik, amelyeket a kristálytani irányokhoz képest úgy vágnak ki, ahogy a vizsgálandó 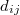együttható mérése megkívánja (kerámia esetén például úgy, hogy a LINK (18) egyenletek valamelyikének megfelelő mechanikai feszültség könnyen megvalósítható-, és a létrejött polarizáció könnyen mérhető legyen).

A direkt effektus alapján történő mérésnél a mintát olyan erőhatásnak teszik ki, aminek hatására megváltozik az anyagnak a hasáb az egyik élével párhuzamos polarizációja. Emiatt a polarizációra merőleges lapokon elhelyezett elektródokon polarizációs töltések (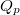 ) jelennek meg. A mérés során ezt a töltést mérik meg, aminek ismeretében a létrejött polarizáció a 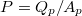összefüggésből kapható meg ( 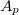az elektródok felületének nagysága). Az inverz piezoelektromos effektus alapján a piezoelektromos állanók a legkézenfekvőbb módon úgy határozhatók meg, hogy a mintát elektromos térbe tesszük (a szemben lévő lapjain elhelyezett elektródokra feszültséget kapcsolunk), és mérjük a mintának a tér hatására bekövetkező deformációját. Egy másik mérési lehetőség az, hogy a mintát egy váltóáramú áramkörbe kapcsoljuk – ekkor a minta a periodikusan változó elektromos térben az inverz piezoelektromos effektus hatására rezgésbe jön – és vizsgáljuk a minta impedanciájának a rezgési frekvenciától való függését.

Mérés a direkt piezoelektromos effektus alapján

Ez a piezoelektromos állandók meghatározásának talán legkorábban alkalmazott módszere. A mérés eredeti változatánál a megfelelő elektródokkal ellátott vizsgálandó mintára meghatározott súlyú testet helyeztek (vagy emeltek le) és közben megmérték a töltés mennyiség megváltozását az elektródokon. Ennek az eljárásnak legfőbb hibaforrásai egyrészt az erőátadás bizonytalanságából, másrészt a töltésmennyiség mérésének nehézségéből adódnak. Sokkal megbízhatóbb a mérés, ha a vizsgálandó mintát periodikusan változó erőhatásnak tesszük ki. Az általunk alkalmazott mérés során periodikus terhelést alkalmazunk.

A vizsgálandó piezoelektromos kerámia esetén a mérés alapját a LINK (18) egyenletek képezik. Ezzel a módszerrel a 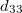együtthatót fogjuk meghatározni, vagyis a LINK (18) egyenletek közül az utolsót kell alkalmaznunk. Ennek megfelelően a mintát úgy kell kialakítani, hogy a nyomóerőt a 3 irányban lehessen működtetni (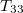), és a keletkező töltést a 3 irányra merőleges lapokon lehessen megmérni (ilyent okoz a 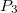megváltozása). Ezt a LINK 2. ábrán látható módon elkészített minta segítségével érhetjük el. Ekkor a mechanikai feszültség és a létrejött polarizáció között az alábbi összefüggés áll fenn:

2. ÁBRA

Feltételezve, hogy a mérés során a töltésveszteség (pl. átvezetés miatt) elhanyagolható, a piezoelektromos polarizáció (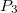) a mintán megjelenő feszültség mérésével határozható meg:

ahol (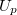) az elektródokon a polarizáció változása által okozott feszültség, a minta kapacitásának és a feszültségmérő bemenetén levő kapacitásnak az eredője, 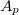pedig a piezoelektromos mintán elhelyezett elektródok felülete. A mintában létrejött feszültséget (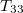) egy, az általa egy mérőrugóban létrehozott alakváltozásból határozzuk meg (l. alább).

A mérőberendezés használata

A mérésnél alkalmazott berendezés blokkvázlatát a LINK 3. ábrán mutatjuk be. A vizsgálandó piezokerámia lapot nyomótalpak közé helyezzük. A nyomótalpak felületei a testtől elszigetelt elektródokká vannak kiképezve, így a mérés során megjelenő töltések a mérőkondenzátorba töltődnek. A mintát terhelő periodikus erőhatást a szolenoid változó mágneses tere által rezgésbe hozott vasmag hozza létre. Az erő mértékének meghatározására a mérőrugó szerepét betöltő konzol deformációját használjuk. A deformációt nyúlásmérő bélyegekkel mérjük. A mérés elvégzéséhez az erőmérőt és a töltésmérő eszközt hitelesíteni kell, amit az alábbi módon végezhetünk el.

Az erőmérő hitelesítése és a nyomófeszültség mérése

Bár a mérés során periodikus erőhatást alkalmazunk, az erőmérő hitelesítését elegendő statikus módszerrel (súlyok felhelyezésével) elvégezni. Ehhez a mérőhíd kimenetére kapcsoljunk digitális multimétert. A mérés megkezdése előtt a nyúlásmérő bélyeg mérőhídját a minta terheletlen állapotában egyenlítsük ki. Ezután zárjuk össze a nyomótalpakat (akár úgy, hogy a piezokerámia már közte van), és a megbízható erőhatás érdekében a beállító csavarral kb. 10 N erővel feszítsük elő a rendszert, és olvassuk le a kimenőfeszültség értékét. Ezután megkezdhetjük a hitelesítést úgy, hogy különböző súlyokat helyezünk el a szolenoid lengő vasmagjához rögzített – erre a célra kiképezett – felületre, és leolvassuk a mérőhíd kimenetén megjelenő feszültséget. A kimenőfeszültséget ( 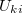) ábrázolva az alkalmazott súly által kifejtett erő függvényében, jó közelítéssel lineáris összefüggést kapunk, és meghatározzuk a pontokhoz illesztett egyenes meredekségét:

Ezzel a mért feszültségből a mintára ható erőt az

összefüggésből számíthatjuk ki ( 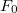az előfeszítést adó erő, pedig az ehhez tartozó kimenőfeszültség). A LINK (20) egyenletben szereplő mechanikai feszültséget a

egyenlet adja meg.

A töltés hitelesítése és a piezoelektromos polarizáció meghatározása

A piezokerámia anyagok általában jelentős relatív permittivitással rendelkező dielektrikumok, így ha egy mintán elektródokat alakítunk ki, számottevő kapacitású piezoelektromos „kondenzátor” jön létre. Elvileg a mechanikai feszültség által létrehozott töltést ezen a „kondenzátoron” is megmérhetnénk, ez a kapacitás azonban általában erősen függ a hőmérséklettől, sőt az alkalmazott feszültségtől is, így a töltést célszerű – a 4. ábrán látható módon – a piezokerámia 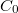kapacitásánál lényegesen nagyobb 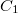mérőkapacitáson fellépő feszültség alapján meghatározni.

4. ÁBRA

A mért 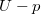feszültségből ekkor a piezoelektromos polarizáció a LINK (21) egyenlet alapján számítható ki

ahol 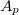a mintán elhelyezett elektródok felülete, és 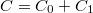. A 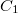mérőkapacitás vagy ismert (gyári adat) vagy értékét méréssel határozzuk meg. A 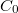kapacitás értékét vagy megmérjük, vagy – ha a minta anyagának permittivitását ismerjük – a síkkondenzátor kapacitására vonatkozó ismert összefüggés segítségével kiszámítjuk.

Mérés periodikus mechanikai feszültség alkalmazásával

A periodikus erő nagyságának változtatása a LINK 3. ábrán vázolt szolenoidra kapcsolt jel amplitúdójának változtatásával történik, és ekkor a nyúlásmérő híd kimenetén váltófeszültség jelenik meg. A polarizáció meghatározására szolgáló mérőkondenzátoron ekkor ugyancsak váltófeszültséget mérünk. A 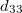piezomodulus a mért 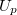és 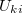feszültségekből a LINK (20), (23), (24) és (25) egyenletek segítségével kapható meg:

Mérési feladatok

• LINK 2.1.5.1 Végezze el a mérőrendszer hitelesítését.
• LINK 2.1.5.2 Határozza meg a kerámia minta piezomodulus értékét két különböző terhelőerő alkalmazásával.

Piezoelektromos állandók mérése az inverz piezoelektromos effektus alapján statikus módszerrel

Az inverz effektus alapján történő mérés egyik lehetséges módja az, hogy a piezoelektromos mintára időben állandó elektromos feszültséget kapcsolunk, és megmérjük a létrejött deformációt. Ez a mérési eljárás a piezomodulusok meghatározására a LINK (19) egyenletek alapján ad módot. Mérésünk során a 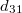állandót fogjuk meghatározni, ezért a LINK (19) egyenletek közül a legelsőt,

használjuk. A mintát most úgy kell kialakítanunk, hogy 3 irányú elektromos teret alkalmazhassunk (az elektródok a 3 irányra merőlegesek legyenek), és mérni tudjuk az 1 irányú megnyúlást (összehúzódást). Mivel a mintában létrejövő térerősség adott elektromos feszültség esetén annál nagyobb, minél vékonyabba minta, a létrejött deformáció pedig arányos a mintának a deformáció irányába eső hosszával, mintaként célszerű a 3 irányban vékony, az 1 irányban pedig hosszú lemezt alkalmazni LINK (5. ábra).

5. ÁBRA

• Piezoelektromos_anyagok_v2