A lap 2015. április 27., 15:32-kori változata (lapforrás) Magyarkuti (vitalap | szerkesztései) ← Régebbi szerkesztés		A lap 2018. február 28., 14:49-kori változata (lapforrás) Zolikk (vitalap | szerkesztései) Újabb szerkesztés →
42. sor:		42. sor:
	A jegyzőkönyvben szerepeljen a program felépítésének leírása, valamint a probléma diszkussziója. Vizsgáljuk meg a kezdeti paraméterek, az inverz hőmérséklet, valamint a paraméterek lépésközeinek hatását az illesztés gyorsaságára és jóságára, azaz adjuk meg, hogy átlagosan hány lépés után illeszkedik a generált függvény az eredetire, valamint mekkora a jellemző minimális energia!		A jegyzőkönyvben szerepeljen a program felépítésének leírása, valamint a probléma diszkussziója. Vizsgáljuk meg a kezdeti paraméterek, az inverz hőmérséklet, valamint a paraméterek lépésközeinek hatását az illesztés gyorsaságára és jóságára, azaz adjuk meg, hogy átlagosan hány lépés után illeszkedik a generált függvény az eredetire, valamint mekkora a jellemző minimális energia!
	Opcionálisan próbáljuk ki, hogy lehetséges-e jobb eredményt elérni, ha $\beta$-t, illetve a lépésközöket dinamikusan változtatjuk! A dokumentációhoz csatoljuk a program forráskódját!		Opcionálisan próbáljuk ki, hogy lehetséges-e jobb eredményt elérni, ha $\beta$-t, illetve a lépésközöket dinamikusan változtatjuk! A dokumentációhoz csatoljuk a program forráskódját!
		+	</wlatex>
		+
		+	= Syllabus in English =
		+
		+	The exercise sample data is available here: [[Média:Data.txt |Data.txt]].
		+
		+	== Introcution ==
		+	Monte Carlo algorithms have a widespread use in many fields, this exercise focuses on fitting a function to a series of data (such as what would be obtained by an experimental measurement). The exercise description presents the necessary theoretical background, and provides indications for the concrete implementation.
		+
		+	== Theoretical background ==
		+	<wlatex>
		+	Let the original series of points we desire to fit, be denoted as $ Y_\textrm{orig}(X_\textrm{i})$, where $i=1\ldots N$. The fitted data series is $Y_\textrm{fit}(X_\textrm{i}, \vec{A})$, where $\vec{A}=(A_1,A_2 \ldots A_\textrm{M})$ is the list of parameters that are varied to obtain the best correlation between the fitted series and the original series. The best fit is to be regarded as a minimization of the following "energy" expression: $$E(\vec{A})=\sum_{i=1}^{N} \left| Y_\textrm{orig}(X_\textrm{i}) - Y_\textrm{fit}(X_\textrm{i}, \vec{A})\right|
		+	\label{MCEnergyEq}
		+	$$
		+	The minimization of energy is obtained through the Monte Carlo - Metropolis algorithm: First, alter the fitting parameters with a random factor: $\vec{A}' = \vec{A}+ \vec{\delta A}$. Using the new randomly varied parameters, a new energy value is obtained: $E(\vec{A}) \rightarrow E(\vec{A}')$. The new parameters should be accepted and kept, if the new energy is closer to the energy minimum, that is, $E(\vec{A}') < E(\vec{A})$. The key to the algorithm is to avoid becoming stuck in a local minimum, thus we use an "annealing" method, where with $p=\textrm{exp}(-\beta(E(\vec{A}')-E(\vec{A})))$ probability we accept the new parameters, even if $E(\vec{A}') > E(\vec{A})$. Observe that using $\beta \rightarrow \infty$ the algorithm can only step downwards in energy, while in the limit $\beta \rightarrow 0$ the walk in the parameter space is entirely random. This gives a physical meaning to the $\beta$ value: it can be regarded as particle moving in the parameter space with $(kT)^{-1}$ inverse temperature.
	</wlatex>		</wlatex>

---

A lap 2018. február 28., 14:49-kori változata

Az alábbi leírás pdf formátumban is letölthető. Példa adatsor: Data.txt.

Tartalomjegyzék 1 Bevezetés 2 Elméleti háttér 3 Implementáció 4 Feladatok

Bevezetés

A Monte Carlo algoritmusok szerteágazó alkalmazási területei közül a függvényillesztés a számítógépes gyakorlat témája. A leírás áttekinti a szükséges elméleti hátteret, valamint segítséget ad a konkrét megvalósításhoz.

Elméleti háttér

Legyen az illesztendő adatsor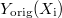 , ahol 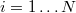. Az illesztett adatsor hasonlóan 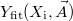, ahol 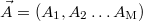a paraméterek listája, amelyek hangolásával érjük el, hogy az illesztett adatsor rásimuljon az eredetire. Ez a következő energiakifejezés minimalizálását jelenti:

A minimalizálást Monte Carlo--Metropolis algoritmussal végezzük: Változtassuk meg a paramétereket véletlenszerűen: 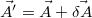. Ezzel a fentiek szerint kiszámolt energia is változik: 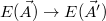. Az új paramétereket elfogadjuk, ha közelebb kerültünk a minimumhoz, tehát 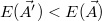. Célunk elkerülni, hogy az algoritmus befagyjon egy lokális minimumba, ezért 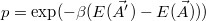valószínűséggel dolgozunk tovább az új paraméterekkel, ha 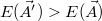. Vegyük észre, hogy 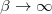esetben csak lefelé léphetünk, míg a 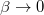határátmenetben véletlenszerű mozgást kapunk a paramétertérben. Ez adja a fizikai jelentését az algoritmusban szereplő értéknek: megfeleltethető egy, a paramétertérben mozgó részecske 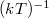inverz hőmérsékletének.

Implementáció

A fentiek megvalósításához a következő felépítést érdemes követni:

1. Készítsünk globális tömböt az eredeti, valamint az illesztett adatsornak;
2. Hasonlóan globális változókban tároljuk az inverz hőmérsékletet, az illesztési paramétereket, valamint azok lépésközét;
3. Deklaráljunk két véletlenszám-generátort: egyet a paraméterek megváltoztatásához és egyet az 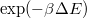valószínűségű lépéshez;
4. Hozzunk létre globális változókat a megváltoztatott paramétereknek, valamint egy tömböt a megváltoztatott paraméterekkel generált illesztőfüggvénynek.

Az illesztés inicializálásához hozzuk létre a szükséges változókat, és olvassuk be a kezdőértékeket a TextBoxokból.

Az illesztést az alábbiak szerint végezzük:

1. Számítsuk ki a 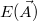szerinti energiát az aktuális változókkal;
2. Változtassuk meg az egyik paramétert a megadott határok között egyenletes eloszlással;
3. Számítsuk ki az így megváltozott energiát;
4. A régi és új energia különbsége alapján döntsünk arról, hogy elfogadjuk-e a változást: ha az új érték kisebb, akkor minden esetben, ha nem, akkor sorsoljunk egy véletlenszámot, és 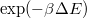valószínűséggel mégis elfogadjuk a változást;
5. Ha szükséges, írjuk ki az új értéket a TextBoxba, és ábrázoljuk a megváltozott illesztőfüggvényt;
6. A fentiek szerint járjunk el a többi paraméter esetében.

Feladatok

Készítsünk grafikus függvényillesztő felületet a data.dat file-ban található 500 elemű adatsor illesztéséhez a 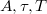függvénnyel, ahol a keresett paraméterek. A cél eléréséhez az alábbiak szerint haladjunk:

1. Olvassuk be és ábrázoljuk a data.dat állomány tartalmát!
2. Hozzunk létre TextBoxokat, amelyekkel állíthatóak a függvényillesztés kiinduló paraméterei, azok lépésköze, valamint az inverz hőmérséklet!
3. Hozzunk létre gombokat, amelyekkel elindíthatjuk a függvényillesztést: legyen lehetséges újraindítani az illesztést a TextBoxokban megadott kezdeti paraméterekkel, valamint 1, illetve 100 illesztési ciklust elindítani!
4. A program jelenítse meg az aktuális paramétereket, az 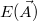szerinti energiát, valamint az illesztett függvényt!

A jegyzőkönyvben szerepeljen a program felépítésének leírása, valamint a probléma diszkussziója. Vizsgáljuk meg a kezdeti paraméterek, az inverz hőmérséklet, valamint a paraméterek lépésközeinek hatását az illesztés gyorsaságára és jóságára, azaz adjuk meg, hogy átlagosan hány lépés után illeszkedik a generált függvény az eredetire, valamint mekkora a jellemző minimális energia! Opcionálisan próbáljuk ki, hogy lehetséges-e jobb eredményt elérni, ha -t, illetve a lépésközöket dinamikusan változtatjuk! A dokumentációhoz csatoljuk a program forráskódját!

Syllabus in English

The exercise sample data is available here: Data.txt.

Introcution

Monte Carlo algorithms have a widespread use in many fields, this exercise focuses on fitting a function to a series of data (such as what would be obtained by an experimental measurement). The exercise description presents the necessary theoretical background, and provides indications for the concrete implementation.

Theoretical background

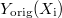Let the original series of points we desire to fit, be denoted as , where 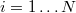. The fitted data series is 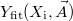, where 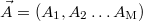is the list of parameters that are varied to obtain the best correlation between the fitted series and the original series. The best fit is to be regarded as a minimization of the following "energy" expression:

The minimization of energy is obtained through the Monte Carlo - Metropolis algorithm: First, alter the fitting parameters with a random factor: 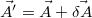. Using the new randomly varied parameters, a new energy value is obtained: 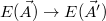. The new parameters should be accepted and kept, if the new energy is closer to the energy minimum, that is, 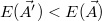. The key to the algorithm is to avoid becoming stuck in a local minimum, thus we use an "annealing" method, where with 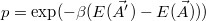probability we accept the new parameters, even if 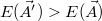. Observe that using 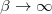the algorithm can only step downwards in energy, while in the limit 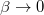the walk in the parameter space is entirely random. This gives a physical meaning to the value: it can be regarded as particle moving in the parameter space with 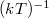inverse temperature.