3. Mérés: RC-körök vizsgálata
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bordacs (vitalap | szerkesztései) 2019. november 1., 20:56-kor történt szerkesztése után volt.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Időben harmonikusan változó jel
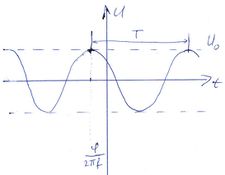
Lineáris áramkörök és harmonikusan változó áram és feszültség jelek részletes tárgyalását lásd a Kisérleti Fizika 1 kurzus rezgésekről szóló fejezetében [1]. A fontosabb mennyiségeket és összefüggéseket alább összefoglaljuk. Az ábrán egy  periodus idővel változó, periodus idővel változó,  =1/ =1/ frekvenciájú feszültség jel látható. Ha a jel amplitúdója frekvenciájú feszültség jel látható. Ha a jel amplitúdója  és fázisa és fázisa  , az időfüggést az alábbi alakban adhatjuk meg: , az időfüggést az alábbi alakban adhatjuk meg:
![\[ U(t)=U_0cos(2\pi ft+\varphi).\]](/images/math/9/6/e/96eab080ec8a57c04dc37fbab0d08b88.png) Hasznos még bevezetni a körfrekvenciát ![\[ U(t)=U_0e^{\omega t+\varphi}=U_0e^\varphi e^{\omega t}.\]](/images/math/c/5/1/c5147ba2c7e1990d294bddc43457b228.png) A harmonikusan változó feszültség a komplex síkon egy |
Lineáris áramköri elemek
Lineáris áramköri elemek esetén az áthajtott áramot és az elemen eső fezsültséget vagy azok deriváltjait lineáris összefüggés kapcsolja össze. Legegyszerűbb ilyen elem az ohmikus ellenállás:
![\[ U=RI \]](/images/math/0/6/3/063b550b153e506421bd709bd6808ca7.png) Az ellenálláson áthaladó áramot az alábbi komplex alakban adhatjuk meg ![\[ I=I_0e^{\omega t}, \]](/images/math/6/e/7/6e761e1350d4f9c0d6559b2100ec7193.png) melyból kiszámíthatjuk a rajta eső feszültsége: ![\[ U=RI_0e^{\omega t}. \]](/images/math/7/1/5/715ddd92f2566ef98d3c7626183d7fe6.png) Tehát az áram és a feszültség fázisa azonos az amplitúdokat pedig a |
Mérési feladatok
1. Feladat
 =2
=2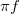 . Az időbeli változást leíró differenciál egyenletek könnyebb kezeléséhez érdemes bevezetni az alábbi komplex változót, melynek valós része adja a mérhető jelet:
. Az időbeli változást leíró differenciál egyenletek könnyebb kezeléséhez érdemes bevezetni az alábbi komplex változót, melynek valós része adja a mérhető jelet:
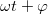 állandó szögsebességgel fordul körbe.
állandó szögsebességgel fordul körbe.
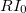 összefüggéssel számolhatjuk ki.
összefüggéssel számolhatjuk ki.