3. Mérés: RC-körök vizsgálata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Időben harmonikusan változó jel
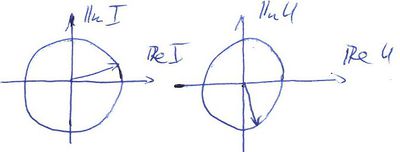
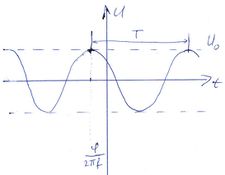
Lineáris áramkörök és harmonikusan változó áram és feszültség jelek részletes tárgyalását lásd a Kisérleti Fizika 1 kurzus rezgésekről szóló fejezetében [1]. A fontosabb mennyiségeket és összefüggéseket alább összefoglaljuk. Az ábrán egy  periodus idővel változó, periodus idővel változó,  =1/ =1/ frekvenciájú feszültség jel látható. Ha a jel amplitúdója frekvenciájú feszültség jel látható. Ha a jel amplitúdója  és fázisa és fázisa  , az időfüggést az alábbi alakban adhatjuk meg: , az időfüggést az alábbi alakban adhatjuk meg:
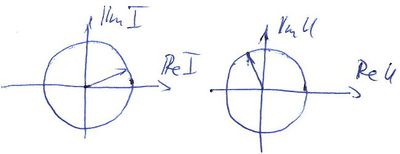
![\[ U(t)=U_0cos(2\pi ft+\varphi).\]](/images/math/9/6/e/96eab080ec8a57c04dc37fbab0d08b88.png) Hasznos még bevezetni a körfrekvenciát ![\[ U(t)=U_0e^{i(\omega t+\varphi)}=U_0e^i\varphi e^{i\omega t}.\]](/images/math/6/c/f/6cf8759b3c8131aeac9699b428fc98e7.png) A harmonikusan változó feszültség a komplex síkon egy |
Lineáris áramköri elemek
Lineáris áramköri elemek esetén az áthajtott áramot és az elemen eső fezsültséget vagy azok deriváltjait lineáris összefüggés kapcsolja össze. Legegyszerűbb ilyen elem az ohmikus ellenállás:
![\[ U=RI \]](/images/math/0/6/3/063b550b153e506421bd709bd6808ca7.png) Az ellenálláson áthaladó áramot az alábbi komplex alakban adhatjuk meg ![\[ I=I_0e^{i\omega t}, \]](/images/math/b/d/b/bdb488bc3e2778d55a33d3ef116d5107.png) melyből kiszámíthatjuk a rajta eső feszültsége: ![\[ Ue^{i\omega t}=RI_0e^{i\omega t}. \]](/images/math/0/d/8/0d8fb867d5d69c2aac8c45bdf2fdc5e9.png) Tehát az áram és a feszültség fázisa azonos az amplitúdokat pedig a |
Egy  induktivitással jellemezhető tekercs esetén a tekercs kapocsain mérhető feszültséget az alábbi képlet adja meg: induktivitással jellemezhető tekercs esetén a tekercs kapocsain mérhető feszültséget az alábbi képlet adja meg:
![\[ U=L\frac{dI}{dt} \]](/images/math/6/a/7/6a711b0266b0467282f7b557a011d032.png) Az időben harmonikusan változó áramot ismét komplex alakban adjuk meg ![\[ I=I_0e^{i\omega t}, \]](/images/math/b/d/b/bdb488bc3e2778d55a33d3ef116d5107.png) melyből a tekercs kapcsain mérhető feszültség: ![\[ Ue^{i\omega t}=i\omega LI_0e^{i\omega t}. \]](/images/math/3/6/a/36a36501bee526a2533ccf5e17cae0e5.png) Tehát a feszültség fázisa |
A  kapacitással jellemezhető kondenzátor esetén ismert, hogy kapacitással jellemezhető kondenzátor esetén ismert, hogy
![\[ Q=CU. \]](/images/math/e/c/3/ec33c1bde7608b580162804655742f21.png) Ezt az összefüggést deriválva és átrendezve a korábbiakhoz hasonló alakú kifejezést kapunk: ![\[ \frac{dU}{dt}=\frac{1}{C}I, \]](/images/math/9/3/a/93ad8959bee68c81cbf1f05351c1ae71.png) hiszen a kondenzátor eltolási árama a töltésváltozással egyenlő. A komplex feszültség-áram összefüggés az alábbi alakot ölti: ![\[ Ue^{i\omega t}=\frac{1}{i\omega C}I_0e^{i\omega t}. \]](/images/math/8/d/b/8db535ea01ab073f095b45769b5e1dea.png) Tehát a feszültség fázisa - |
Mérési feladatok
1. Feladat A próbapanelen állítsunk össze egy  =10 k
=10 k ellenállásból és az ismeretlen
ellenállásból és az ismeretlen  kapacitású kondenzártorból (barna áramköri elem) álló soros kapcsolást.
kapacitású kondenzártorból (barna áramköri elem) álló soros kapcsolást. 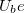 bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre f=1\,kHz frekvenciájú,
bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre f=1\,kHz frekvenciájú, 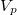 p=1\,V-os szinusz jelet. A bemeneti és a kondenzátoron eső Uki kimeneti feszültséget kapcsoljuk a mérőkártya AI 0+, AI 0- és AI 1+, AI 1- csatlakozói közé. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást valamint a triggert.
p=1\,V-os szinusz jelet. A bemeneti és a kondenzátoron eső Uki kimeneti feszültséget kapcsoljuk a mérőkártya AI 0+, AI 0- és AI 1+, AI 1- csatlakozói közé. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást valamint a triggert.
\begin{figure}[h!] \begin{center} \includegraphics[width=10 cm]{RC.png} \caption{} \end{center} \end{figure}
Rögzítsük mindkét csatornán a feszültség időfüggését, majd az oszcilloszkóp program STOP gombjának megnyomasa után, a LOG gomb segítségével mentsük el a mért jelalakokat. Az IGOR segítségével olvassuk be a jeleket. (A loadwaves/tweaks menu beállításai: az összes elválasztó jelet ki kell pipálni, date format: year.month.day, line containing column label: 2, first line containing data: 5.) A data/change wave scaling menüvel állítsuk be az időtengely lépésközét. (Figyelem az oszcilloszkóp időalapjának változtatásával változik a skálázás is!) Illesszünk szinusz görbét, és az illesztésből határozzuk meg a két jel amplitúdójának arányát, illetve a fázisuk különbséget. Számítsuk ki az ismeretlen C kapacitást és becsüljük meg a mérés hibáját. Végezzük el a fenti mérést 100 Hz-en, 330 Hz-en, 3.3 kHz-en és 10 kHz-en is. A mért amplitúdó arányokat és fáziskülönbségeket a frekvencia logaritmusának függvényében ábrázoljuk. Miért nevezik ezt a kapcsolást aluláteresztő szűrőnek?
 =2
=2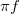 . Az időbeli változást leíró differenciál egyenletek könnyebb kezeléséhez érdemes bevezetni az alábbi komplex változót, melynek valós része adja a mérhető jelet:
. Az időbeli változást leíró differenciál egyenletek könnyebb kezeléséhez érdemes bevezetni az alábbi komplex változót, melynek valós része adja a mérhető jelet:
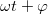 állandó szögsebességgel fordul körbe.
állandó szögsebességgel fordul körbe.
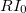 összefüggéssel számolhatjuk ki.
összefüggéssel számolhatjuk ki.
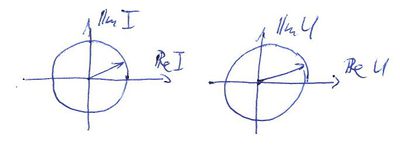
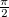 -vel eltolódik az áramhoz képest, az amplitúdokat pedig a
-vel eltolódik az áramhoz képest, az amplitúdokat pedig a 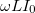 összefüggéssel számolhatjuk ki. Érdemes bevezetni az ellenálláshoz hasonló fogalmat, az impedanciát. Ez a komplex mennyiség lineáris áramkörökben megadja a feszülség és az áram komplex arányát. Induktivitás esetén
összefüggéssel számolhatjuk ki. Érdemes bevezetni az ellenálláshoz hasonló fogalmat, az impedanciát. Ez a komplex mennyiség lineáris áramkörökben megadja a feszülség és az áram komplex arányát. Induktivitás esetén 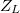 =
=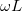 .
.
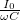 összefüggéssel számolhatjuk ki. A kondenzátorhoz tartozó impedancia
összefüggéssel számolhatjuk ki. A kondenzátorhoz tartozó impedancia 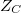 =
=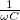 .
.