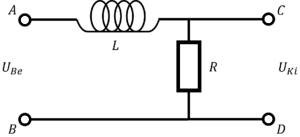Harmonikus rezgések vizsgálata
A mérés célja:
- elmélyíteni a hallgatók harmonikus rezgésekről szóló ismereteit,
- megtapasztalni a mechanikai és az elektromos rezgések közötti analógiát,
- megismerkedni a váltóáramú mérésekkel és a komplex jelöléssel,
- valamint egyszerű szűrőkapcsolások tulajdonságaival
Ennek érdekében:
- a mechanikai rezgések leírásán keresztül áttekintjük a harmonikus rezgések elméletét,
- megismerjük a különböző áramköri elemek váltóáramú viselkedését,
- áttekintjük a komlex jelölést
- megismerkedünk néhány egyszerű szűrőelrendezéssel,
- megvizsgáljuk a mechanikai rezgéseket,
- méréseket végzünk alul- és felüláteresztő szűrőkkel,
- megvizsgáljuk a feszültségviszonyokat soros RLC körökben,
- megfigyeljük az analógiát a soros RLC és a mechanikai rezgések között.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul. A harmonikus rezgés tulajdonságait a mechanikai rezgések példáján keresztül tárgyaljuk, majd megmutatjuk a soros RLC körökben megfigyelhető elektromos rezgések és a mechanikai rezgések közötti analógiát. Végül pedig bevezetjük a komplex jelölést és megvizsgálunk néhány egyszerű szűrőelrendezést.
Harmonikus mechanikai rezgések leírása
Csillapítatlan mechanikai rezgések
Ha egy  tömegű anyagi pontra a kitéréssel arányos, rugalmas erő hat, akkor a mozgásegyenlet
tömegű anyagi pontra a kitéréssel arányos, rugalmas erő hat, akkor a mozgásegyenlet
![\[ma=-Dx\]](/images/math/f/b/3/fb30b4da9009aab1cbabab9dff6513fa.png)
alakú, ahol  a rugóállandó,
a rugóállandó,  a tömegpont kitérése az egyensúlyi helyzetből,
a tömegpont kitérése az egyensúlyi helyzetből,  a tömeg, és
a tömeg, és  a gyorsulás.
A mozgásegyenlet megoldása
a gyorsulás.
A mozgásegyenlet megoldása
![\[x(t)=A\sin(\omega_0 t+\alpha)\]](/images/math/6/9/8/698d670dcace95562a59318f4bc511f6.png)
ahol  a (kitérési) amplitúdó,
a (kitérési) amplitúdó,  a
a  időpillanathoz tartozó fázis (mindkettőt a kezdeti feltételek határozzák meg),
időpillanathoz tartozó fázis (mindkettőt a kezdeti feltételek határozzák meg),
![\[\omega_0=\sqrt{\frac{D}{m}}\]](/images/math/6/2/b/62b794d7c5bd9b0793952f4288745739.png)
a csillapítatlan rezgő rendszer körfrekvenciája. (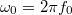 , ahol
, ahol  a megfelelő frekvencia.)
a megfelelő frekvencia.)
A harmonikus rezgőmozgás sebessége
![\[v(t)=\frac{\text{d} x}{\text{d} t}=A\omega_0\cos(\omega_0 t+\alpha)\]](/images/math/9/d/c/9dcad6f28870846c89ba112d12dd1f58.png)
ahol 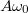 a maximális sebesség, az ún. sebességamplitúdó.
a maximális sebesség, az ún. sebességamplitúdó.
Csillapodó rezgések
A csillapodást okozó erők gyakran (jó közelítéssel) a sebességgel arányosak: 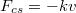 , ahol
, ahol  a csillapítás erősségére jellemző mennyiség. Ekkor a tömegpont mozgásegyenlete:
a csillapítás erősségére jellemző mennyiség. Ekkor a tömegpont mozgásegyenlete:
![\[ma=-Dx-kv\]](/images/math/b/7/0/b70cad48363b12ebe7c00c8de056d4b1.png)
ami a 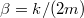 csillapítási tényező bevezetésével és
csillapítási tényező bevezetésével és  definíciójának felhasználásával az alábbi alakra hozható:
definíciójának felhasználásával az alábbi alakra hozható:
![\[\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=0\]](/images/math/3/3/f/33fca78ee06fe71af4452fd72c08965a.png)
A differenciálegyenlet megoldása 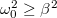 esetén időben csökkenő amplitúdójú lengéseket eredményez:
esetén időben csökkenő amplitúdójú lengéseket eredményez:
![\[x(t)=Ae^{-\beta t}\sin(\omega' t+\alpha)\]](/images/math/1/6/a/16aac187848ca1c99ebe5aaba1c45d99.png)
A rezgés körfrekvenciája
![\[\omega'=\sqrt{\omega_0^2-\beta^2}\]](/images/math/c/6/3/c630d6c795ef05121257c9d49adecb90.png)
Az amplitúdóváltozás jellemzésére különböző mennyiségeket használnak. A csillapodási hányados két, azonos irányban egymás után következő amplitúdó hányadosa
![\[K=\frac{x_n}{x_{n+1} }=e^{\beta T}\]](/images/math/d/7/5/d75e89c8fe55114bbb46e0c7a217c899.png)
ahol 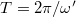 . Használatos még a K csillapodási hányados logaritmusa, az ún. logaritmikus dekrementum is:
. Használatos még a K csillapodási hányados logaritmusa, az ún. logaritmikus dekrementum is:
![\[\Lambda=\ln K=\beta T\]](/images/math/f/5/5/f55922b2e6f73cf0584aa6742023ae9d.png)
Kényszerrezgések
Egy  tömegre pl. motor és excenter segítségével időben periodikusan változó erőt alkalmazva egy átmeneti időszak után időben állandósult rezgés alakul ki, melynek frekvenciája megegyezik a kényszerítő erő frekvenciájával, míg amplitúdója függ az erőtől, a rugóállandótól, a tömegtől, a csillapítástól valamint a gerjesztő frekvenciától. Az anyagi pont mozgásegyenlete ekkor:
tömegre pl. motor és excenter segítségével időben periodikusan változó erőt alkalmazva egy átmeneti időszak után időben állandósult rezgés alakul ki, melynek frekvenciája megegyezik a kényszerítő erő frekvenciájával, míg amplitúdója függ az erőtől, a rugóállandótól, a tömegtől, a csillapítástól valamint a gerjesztő frekvenciától. Az anyagi pont mozgásegyenlete ekkor:
![\[ma=-Dx-kv+F_0\sin(\omega t)\]](/images/math/d/7/0/d700dd523f6789794008013701d4127e.png)
A korábban bevezetett jelöléseket alkalmazva másodrendű lineáris, inhomogén differenciálegyenletet kapunk:
![\[\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=\frac{F_0}{m}\sin(\omega t)\]](/images/math/a/3/6/a365b484e2e8bca8da1b9e33b1dc9748.png)
ahol 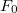 a kényszererő maximális értéke. Az egyenlet megoldása:
a kényszererő maximális értéke. Az egyenlet megoldása:
![\[x(t)=A_0e^{-\beta t}\sin(\omega' t+\alpha)+\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} }\sin(\omega t+\varphi),\]](/images/math/0/0/9/00954c33ce0f7e021cd0b585b36be497.png)
melynek második tagja írja le az állandósult állapotot. Az állandósult állapot amplitúdója:
![\[A(\omega)=\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} },\]](/images/math/7/7/2/7720f8a65b3abb6e065f1f3b8160c243.png)
melynek maximuma van az
![\[\omega_{max}=\sqrt{\omega_0^2-2\beta^2}\]](/images/math/9/1/5/915a5a394448e94f7f6df72c7607febb.png)
körfrekvenciánál. A  fázisállandó nem az időmérés kezdetétől függ, hanem a kényszerítő erő fázisától való eltérés, ennek tangense:
fázisállandó nem az időmérés kezdetétől függ, hanem a kényszerítő erő fázisától való eltérés, ennek tangense:
![\[\text{tg}\varphi=\frac{2\beta\omega}{\omega_0^2-\omega^2}.\]](/images/math/6/d/b/6dbbdd1f06cca90c8f59865a19ee8340.png)
Az amplitúdóhoz hasonlóan megadhatjuk a sebességamplitúdó kifejezését is:
![\[A\omega=\frac{F_0\omega}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}}\]](/images/math/a/c/4/ac40d1467d7453e71cd74c80e41715d4.png)
melynek maximuma – ellentétben a kitérési amplitúdó maximumával – éppen  -nál van, ahol
-nál van, ahol
![\[A\omega_0=\frac{F_0}{2m\beta}.\]](/images/math/3/c/3/3c369dfa228035d26cc0c23371ffe361.png)
A kényszerrezgés energiaviszonyainak jellemezésére az egy periódus alatt disszipált energia 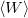 és a rendszerben tárolt átlagos energia
és a rendszerben tárolt átlagos energia 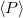 hányadosával arányos jósági tényezőt használjuk
hányadosával arányos jósági tényezőt használjuk
![\[Q=2\pi\frac{\langle W\rangle}{T\langle P\rangle}\approx\frac{\omega_0}{2\beta}\]](/images/math/0/0/b/00b44b97ac127fd01604257e56fe2fc0.png)
Váltakozó áramú kapcsolások
Áramköri elemek áram- és feszültségviszonyai
Ohmos ellenállás
Az ellenálláson eső feszültséget az
![\[u(t)=R i(t)\]](/images/math/5/b/3/5b3eacca33f2f21f61fce5be60d9610c.png)
összefüggés írja le. Szinuszos gerjesztés [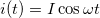 ] esetén
] esetén
![\[u(t) = R I \cos\omega t,\]](/images/math/5/6/0/56086c4fb6b9c471180784a7e7cc0c98.png)
azaz az ohmos ellenálláson a feszültség és az áram azonos fázisban van.
Tekercs
A tekercsben indukálódó feszültséget az
![\[u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}\]](/images/math/7/0/d/70d81694316981734d9306478ac2b228.png)
egyenlet írja le. Szinuszos gerjesztés [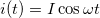 ] esetén
] esetén
![\[u(t) = -L \omega I \sin\omega t = L \omega I \cos( \omega t + 90^\circ),\]](/images/math/2/7/8/27847fbdff5ee243ad40e044038bd4ab.png)
tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest.
Kondenzátor
A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:
![\[i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}.\]](/images/math/2/a/d/2ad4b9dbaa6debb8b51c07b374b84fdf.png)
Szinuszos gerjesztés [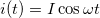 ] esetén:
] esetén:
![\[u(t) = \frac{I}{C\omega}\sin\omega t = \frac{I}{C\omega}\cos(\omega t - 90^\circ),\]](/images/math/c/4/8/c482906f41df3b5cf8a9c151f6eb53ff.png)
azaz a kondenzátor feszültsége 90°-kal késik az áramhoz képest.
Soros rezgőkör - a mechanikai kényszerrezgés elektromos megfelelője
Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (1. ábra). Az alábbiakban láthatjuk, hogy ez az áramkör a korábban ismertetett kényszerrezgés elektromos megfelelője, amennyiben a tömegpont kitérését megfeleltetjük a kondenzátor töltésének, a rugóállandót a kondenzátor kapacitásának, a tömegpont tömegét a tekercs induktivitásának és a csillapítást az ellenállásnak. Ha az RLC körben a kondenzátort feltöltenénk, majd a bemenetet rövidre zárnánk, akkor egy csillapodó rezgést figyelhetnénk meg. A nagy frekvencia és a gyors csillapodás miatt azonban ezt nehezebb megfigyelni, mint egy kitérített, és magára hagyott mechanikai rezgő rendszert. Ha a bemenetre szinuszos gerjesztő feszültséget kapcsolunk, akkor viszont a kényszerrezgéssel teljesen analóg viselkedést figyelhetünk meg.
Viszgáljuk meg a rezgőkör differenciálegyenletét a kondenzátor időfüggő töltésére (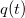 ) felírva, amikor a rezgőkörre
) felírva, amikor a rezgőkörre 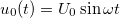 feszültséget kapcsolunk:
feszültséget kapcsolunk:
![\[u_{\rm C}=q(t)/C\]](/images/math/6/e/5/6e557c5a7c02f41f9e8b70185a9b0687.png)
![\[i(t)=\dot{q}(t)\]](/images/math/3/4/5/345f04f2a83cf0399cf9dc740f7a3cc0.png)
![\[u_{\rm R}=Ri(t)=R\dot{q}(t)\]](/images/math/0/f/9/0f98abcde80a186b296ccde6f3a37145.png)
![\[u_{\rm L}=L\dot{i}(t)=L\ddot{q}(t)\]](/images/math/4/1/1/41175632a87ec6b612a0336e39d0926c.png)
![\[L\ddot{q}(t)+R\dot{q}(t)+q(t)/C=U_0\sin\omega t\]](/images/math/8/f/e/8fe0fb39e34df6fdeb9a07c794faa834.png)
![\[\ddot{q}(t)+\frac{R}{L}\dot{q}(t)+\frac{1}{LC}q(t)=\frac{U_0}{L}\sin\omega t.\]](/images/math/d/3/c/d3ce0c79341d4c23d3824118773ab42e.png)
Vegyük észre, hogy ez a differenciálegyenlet 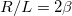 és
és 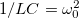 jelöléssel a kényszerrezgést leíró differenciálegyenlettel teljesen analóg egyenletet eredményez. Ennek következtében az általános megoldás is teljesen analóg: traniens és állandósult tagokat tartalmaz.
jelöléssel a kényszerrezgést leíró differenciálegyenlettel teljesen analóg egyenletet eredményez. Ennek következtében az általános megoldás is teljesen analóg: traniens és állandósult tagokat tartalmaz.
Esetünkben a tranziens tag hamar elhal, és az állandósult tagot tanulmányozhatjuk. Az amplitúdó itt a kondenzátor töltése, de számunkra sokkal érdekesebb ennek deriváltja, a körben folyó áramerősség. Ez tehát az analógia alapján a mechanikai rezgés sebességrezonanciájával egyezik meg:
![\[I(\omega)=\frac{U_0}{L\sqrt{\left(\omega^2-\omega_0^2\right)^2+4\beta^2\omega^2}}.\]](/images/math/4/3/a/43a8a3f9f64b2cde816dccbf4d03ee63.png)
Ha behelyettesítjük  és
és  értékét, akkor
értékét, akkor
![\[I(\omega)=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}.\]](/images/math/b/7/f/b7f728d8b68397856b7e50ba9f6cea9a.png)
Látható, hogy a rezgőkörben folyó áramnak 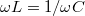 esetén az
esetén az
![\[\omega_0 = \frac{1}{\sqrt{LC}}\]](/images/math/a/d/4/ad4a43ecaf657200d72e8c141af15534.png)
körfrekvencián maximuma van. A jelenséget rezonanciának,  -t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián áramrezonancia alakul ki.
-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián áramrezonancia alakul ki.
Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymáshoz viszonyítva 180°-os fázisban vannak, abszolút értékük pedig megegyezik (hiszen azonos áram folyik át rajtuk), így egymást kiegyenlítik.
Megjegyzés: A kondenzátoron és a tekercsen eső feszültségnek nem pontosan az  rezonanciafrekvencián van maximuma - hasonlóan a mechanikai kényszerrezgés amplitúdórezonanciájához.
rezonanciafrekvencián van maximuma - hasonlóan a mechanikai kényszerrezgés amplitúdórezonanciájához.
Komplex jelölés
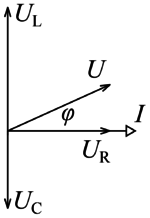
Szinuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos  körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az 2. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.
körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az 2. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.
Az áramkörre kapcsolt feszültség a három, sorbakapcsolt feszültséget jelölő fazor vektori eredője.
A fazorokat felfoghatjuk komlex számokként is. Így az egyes áram és feszültségjeleket egy-egy komplex szám jelöli. A fazorokhoz hasonlóan a komplex szám abszolút értéke a jel nagyságát (csúcsértékét), a komplex szám arkusza pedig a jel (a kiválasztott fázishelyzethez viszonyított) fázisát adja meg.
Figyelem! Mivel a villamos hálózatoknál 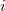 az áram pillanatértékét jelöli, a komplex egység szokásos jelölése itt
az áram pillanatértékét jelöli, a komplex egység szokásos jelölése itt  !
!
Az 2. ábrán látható fazorábrán szereplő jeleknek megfelelő komplex mennyiségek:
![\[\mathbf{I}=I\]](/images/math/d/b/3/db3b10836f663e18d0b2457c4f381161.png)
![\[\mathbf{U_{\rm R}}=U_{\rm R}=RI\]](/images/math/6/d/e/6dea4cee9d301924a744b4a8c84a41ec.png)
![\[\mathbf{U_{\rm L}}=jU_{\rm L}=j\omega LI\]](/images/math/4/0/4/404442f2e57583da99a06b8decbb04df.png)
![\[\mathbf{U_{\rm C}}=-jU_{\rm C}=I/j\omega C\]](/images/math/5/0/2/502eb5b1ee2c68e4c415bc5288d65148.png)
Ekkor az eredő (komplex) feszültséget nem csak megszerkeszthetjük, hanem egyszerű komplex algebrával ki is számolhatjuk:
![\[\mathbf{U} = \mathbf{U_{\rm R}}+\mathbf{U_{\rm L}}+\mathbf{U_{\rm C}}= RI + j\omega LI + I/j\omega C\]](/images/math/6/6/4/6641a34eef0fb3219e31270b1ff325ca.png)
Az eredő feszültség nagysága (csúcsértéke) a komplex érték abszolút értéke:
![\[U=|\mathbf{U}|=\sqrt{R^2+(\omega L-1/\omega C)^2}I=ZI,\]](/images/math/a/4/c/a4cd1a16c71b0e334e88ba1acfcabfd1.png)
ahol 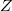 az eredő ellenállás.
az eredő ellenállás.
Az eredő feszültség fázisa a komplex feszültség arkusza:
![\[\varphi=\arccos\frac{R}{Z}.\]](/images/math/7/3/d/73dfbd65becf4c14d17054046e02c2d1.png)
A komplex áram és feszültség alapján azonban közvetlenül is fel tudjuk írni az áram és a feszültség időfüggvényét:
![\[i(t)=\rm{Re}\left(\mathbf{I}e^{j\omega t}\right)=I\cos \omega t\]](/images/math/b/6/8/b68fbcf4e38afed4b745c41ad35ae592.png)
![\[u(t)=\rm{Re}\left(\mathbf{U}e^{j\omega t}\right)=U\cos(\omega t+\varphi)=ZI\cos(\omega t+\varphi)\]](/images/math/d/7/b/d7bced5d7c0296acffc3b72671e50b2e.png)
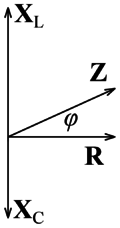
Ha az 2. ábrán látható fazorokat leíró komplex feszültségeket elosztjuk az áramerősség nagyságával, akkor ellenállás dimenziójú komplex mennyiségeket kapunk:
![\[\frac{\mathbf{U_{\rm R}}}{I}=\mathbf{R}=R\]](/images/math/2/0/d/20d4bff2b98a0110a9592b1262724367.png)
![\[\frac{\mathbf{U_{\rm L}}}{I}=\mathbf{X_{\rm L}}=j\omega L\]](/images/math/9/0/9/909749c3b65f94d726bfe561cccd17ed.png)
![\[\frac{\mathbf{U_{\rm C}}}{I}=\mathbf{X_{\rm C}}=1/j\omega C\]](/images/math/4/b/6/4b6488db0f72daa07f669e9634fad5ac.png)
![\[\frac{\mathbf{U}}{I}=\mathbf{Z}\]](/images/math/7/5/4/754bfd62ff79474ca4fe652ca9bf87df.png)
A komplex ellenállásokkal ugyanúgy számolhatunk egy váltóáramú körben, mint az ohmos ellenállásokkal egyenáramú hálózatok esetében.
A mi esetünkben a soros kapcsolás miatt az eredő (komplex) ellenállás az egyes (komplex) ellenállások összege:
![\[\mathbf{Z}=\mathbf{R}+\mathbf{X_{\rm L}}+\mathbf{X_{\rm C}}.\]](/images/math/3/4/8/348ecc64ebd75571a424645a09bb1775.png)
A komplex jelölésmóddal bármely áramköri elem leírása olyan, mintha egy ohmos ellenállás lenne:
![\[\mathbf{U_{\rm R}}=\mathbf{R}\mathbf{I}\]](/images/math/6/f/9/6f983d04136f9b37d69e64e469e822a4.png)
![\[\mathbf{U_{\rm L}}=\mathbf{X_{\rm L}}\mathbf{I}\]](/images/math/a/9/5/a95ad0be1fe4306378c8ec89f23f6bbf.png)
![\[\mathbf{U_{\rm C}}=\mathbf{X_{\rm C}}\mathbf{I}\]](/images/math/5/e/3/5e3f95af623562cd52e17a7ce9d424ae.png)
![\[\mathbf{U}=\mathbf{Z}\mathbf{I}\]](/images/math/9/d/8/9d836ab019d68fc534654b71bb9da238.png)
A komplex ellenállás abszolút értéke a skalár ellenállás értéket adja, míg arkusza azt mutatja meg, hogy az adott áramköri elem mennyivel tolja el a fázist.
Egyszerű áramkörök leírása komplex jelöléssel
A komplex leírásmód előnyének szemléltetése céljából az alábbiakban megvizsgálunk néhány negyszerű áramkört.
Szűrő áramkörök
Szűrők segítségével egy különböző frekvenciájú rezgésekből álló elektromos jelből ki lehet szűrni bizonyos frekvenciatartományokat. A legegyszerűbb elsőrendű szűrők egy ellenállást és egy kondenzátort/tekercset tartalmaznak és a feszültségosztás elvén működnek, melyet a komplex jelölést felhasználva egyszerűen az egyenáramú áramkörökben jól ismert 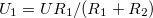 feszültségosztó képlettel leírhatunk komplex ellenállások használatával. Ilyen szűrőkre láthatunk példát az 4/a és 4/b ábrákon. A kapcsolások feszültségviszonyai pedig az alábbi képletekkel írhatók le (A vastag betűs mennyiségek komplex változók,
feszültségosztó képlettel leírhatunk komplex ellenállások használatával. Ilyen szűrőkre láthatunk példát az 4/a és 4/b ábrákon. A kapcsolások feszültségviszonyai pedig az alábbi képletekkel írhatók le (A vastag betűs mennyiségek komplex változók,  a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!):
a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!):
![\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega RC} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega RC}\right|=\frac{1}{\sqrt{1+(\omega RC)^2}} \end{array} \]](/images/math/9/4/3/943854eb463ad63e4d67664743f7e96e.png) |
![\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{R}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega L/R} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega L/R}\right|=\frac{1}{\sqrt{1+(\omega L/R)^2}} \end{array} \]](/images/math/5/f/1/5f1da1dd24d313e4abefdadb0d7af81c.png) |
A kimeneti és bemeneti feszültségek hányadosa, a hálózatra jellemző, frekvenciafüggő kifejezés, melyeket megvizsgálva látható, hogy formailag azonosak, tehát a két kapcsolás azonos jellegű viselkedést mutat. Ameddig 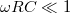 vagy
vagy 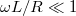 , a kifejezések értéke 1; ha
, a kifejezések értéke 1; ha 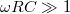 vagy
vagy 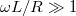 , a hányados értéke
, a hányados értéke 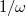 szerint csökken. Ez azt jelenti, hogy adott
szerint csökken. Ez azt jelenti, hogy adott  ,
,  és
és  esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.
esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.
Könnyen belátható továbbá az is, hogy ugyanezeket az elrendezéseket használva felüláteresztő szűrőket is megvalósíthatunk, amennyiben a kondenzátoron (4/a) vagy ellenálláson (4/b) eső feszültség helyett a kapcsolás másik áramköri elemén (ellenállás/tekercs) eső feszültséget tekintjük kimeneti feszültségnek.
Rezgőkörök
A Komplex jelölést bemutató fejezetben egy soros rezgőkör állandósult állapotát írtuk fel a komplex jelölés használatával (fontos megjegyezni, hogy a tranzienseket ebben a leírásban nem lehet vizsgálni), ahol a hálózat eredő impedanciájára:
![\[\mathbf{Z}(\omega) = j\omega L + 1/j\omega C + R,\]](/images/math/6/5/d/65dbf7d7077c874dad04faae24313177.png)
az impedancia abszolút értékére és fázisszögére pedig:
![\[Z(\omega) = \sqrt{(\omega L-1/\omega C)^2+R^2}\]](/images/math/a/f/b/afb8959afc8675cd549498ff967704b1.png)
![\[\varphi = \arccos\frac{R}{Z},\]](/images/math/8/2/2/82221f86e8309757526500d10336dd6b.png)
összefüggéseket kaptuk.
Így a körben folyó áram (azaz az ellenálláson eső feszültség és az ellenállás hányadosa):
![\[I(\omega)= \frac{U_R}{R}= \frac{U_0}{Z}=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}\]](/images/math/e/4/5/e45acdf928616e709a20c61d006c9342.png)
A komplex felírásmód alkalmazásával hasonlóan egyszerűen megkaphatjuk egy párhuzamos LC rezgőkör jellemzőit is, melyek az alábbiak:
![\[\mathbf{Z}(\omega) = \frac{j\omega L}{ 1 - \omega^{2} L C} + R,\]](/images/math/0/1/b/01b3e2b9cff9ccab092936c7257bdcb3.png)
![\[Z(\omega) = \sqrt{\frac{\omega^{2} L^{2}}{(1 - \omega^{2} L C)^2} + R^{2}}\]](/images/math/3/1/7/3175c1c4d456032ef19e4f36857da724.png)
![\[I(\omega)= \frac{U_0}{Z}=\frac{U_0}{\sqrt{R^2 + \omega^{2} L^{2} / (1 - \omega^{2} L C)^2}}\]](/images/math/e/9/0/e9047f438372cf732dfcb41615453220.png)
A körben folyó áramot leíró képlet elemzéséből megállapítható, hogy a párhuzamos RLC kör esetén kis és nagy  értékeknél kapunk maximális áramot és az áramnak mimimuma van
értékeknél kapunk maximális áramot és az áramnak mimimuma van  függvényében az
függvényében az 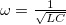 helyen.
helyen.
A méréshez használt eszközök=
A mechanikai rezgések vizsgálatához használt kísérleti berendezés leírása
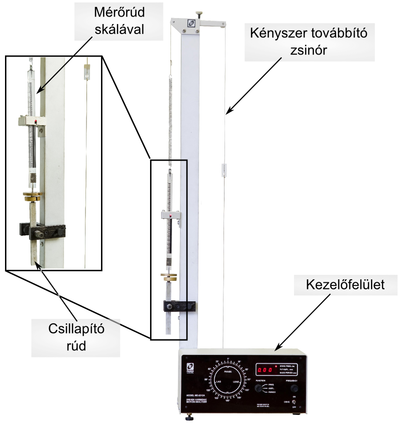
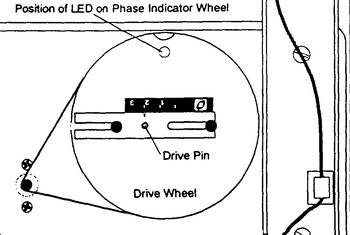
A kísérleti berendezés az 6. ábrán láthatóhoz hasonló saját gyártású mérőeszköz. Az alul elhelyezkedő elektronikai egységben található a meghajtó villanymotor és egy optikai érzékelő, mellyel a meghajtás frekkvenciája mérhető, az egység első lapján találhatók az elektromos csatlakozók (motortáp, optikai értzékelő tápja, illetve jelkimenete), illetve a kényszererőt létrehozó excenter. A kényszererő amplitúdója az amplitúdórúd helyzetének változtatásával szabályozható, ami a kényszert kifejtő zsinór rögzítési pontja és az excenter középpontja közötti távolságot befolyásolja (7. ábra). A kényszert továbbító zsinór a tartóoszlop tetején található két csiga vájatain áthaladva egy hurokkal kapcsolódik a vizsgálandó rugó egyik végéhez. A másik véghez a skálával ellátott mérőrúd és a hozzá erősített ún. csillapító rúd csatlakozik. E két rúd alkotja a rezgőmozgást végző „alaptömeget”, melynek értéke 50 g.
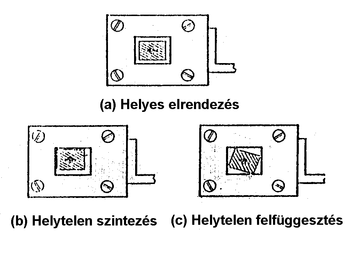
A mérőkészlethez tartozik két 50 g tömegű rézkorong is. A korongokat a mérőrudat és csillapitórudat összekötő csavarmenetre lehet felerősíteni. A tartóoszlop középmagasságánál látható a rúdvezető, mérőrudat a rúdvezető téglalap alakú nyílásán kell átvezetni úgy, hogy a mérőrúd egyik oldala sem ér hozzá a rúdvezető nyílásának falához (8. ábra). A nem jó a beállítás a 9. ábrán látható „b” vagy „c” esetben fordul elő. A „b” esetet az elektronika doboz változtatható magasságú lábainak megfelelő állításával korrigálhatjuk (vízszintezés). A „c” eset a mérőrúd felfüggesztésével (elcsavarásával)javítható.
Helyes beállítás esetén a rezgés csillapodása – melyet a légellenállás ill. a berendezés egyes elemei között fellépő súrlódás okoz – igen kicsi. Ezért a csillapítás változtatása (növelése) céljából a tartórúdra egy olyan mágnespárt szerelhetünk fel, melynek pofái között a távolság változtatható. Ezen mágnespofák között mozog az alumíniumból készült csillapítórúd. A mágneses tér hatására a mozgó fémrúdban örvényáramok keletkeznek, melyek Joule-hőjének disszipációja okozza a rendszer csillapodását. A mágnespofák közötti távolság csökkentésével a mágneses térerősség növelhető, azaz a disszipáció, vagyis a csillapítás fokozható.
A motor egy szabályozható tápegységgel kerül meghajtásra, és a feszültség változtatásával érhetjük el a meghajtás frekvenciájának változását. A mérőrúd pozícióját az idő függvényében (így a rezgés amplitúdóját és frekvenciáját is) egy Vernier GO! Motion ultrahangos távolságmérővel méri a Logger Lite nevű program segítségével (ha saját laptopot szeretne használni a méréshez, akkor telepítse a programot). A meghajtás frekvenciáját mérő optikai jeladó feszülségjele szintén rögzíthető a Logger Lite programban. Az optikai jeladó használatához egy 5V-os DC tápfeszültséget kell kapcsolni a tápbemenetre, melyet szintén a rendelkezésre álló tápegyből tud kivenni. FIGYELEM! A mérésnél a két szenzort egyszerre kell a számítógéphez csatlakoztatni, ehhez két szabad USB port szükséges! Ha a saját laptopja nem rendelkezik két USB-vel és megfelelő USB bővítője sincs, akkor azt mérés előtt jelezze a mérésvezetőknek!
National Instruments myDAQ adatgyűjtő kártya
A váltóáramú körök méréséhez egy National Instruments myDAQ adatgyűjtőkártyát fog használni, melyet a Matlabbal vezérel. A myDAQ kártya rendelkezik 2-2 db +-10V-os analóg, 1-1db audió, 8db digitális ki- és bemenettel, valamint 5V-os és +-15V-os tápfeszültség kimenettel és digitális multiméter funkcióval. Jelen méréshez a fenti funkciók közül egy analóg kimenetetés két analóg bemenetet használunk.
A mérőkártya programozásával későbbi tanulmányai során fog megismerkedni, jelen labor keretében az alábbi előre elkészített függvényekkel fog dolgozni, melyek elvégzik a mérőkártya konfigurálását és a jelek kiadását/adatgyűjtés:
- A myDAQ_init nevű függvénnyel tudja elvégezni a mérőkártya inicializálását a mérés elején, azaz konfigurálja az "AO0" kimeneti, valamint az "AI0" és "AI1" bemeneti csatornákat, illetve beállítja a 200kHz-es mintavételezési frekvenciát. Ezt a függvényt csak egyszer szükséges meghívni (kivéve, ha újraindítja a Matlab-ot).
- A myDAQ_arb_rw függévénnyel egy tetszőleges pontonként definiált jelet tud a kártya "AO0" csatornáján kiadni, miközben az "AI0" és "AI1" csatornákon mintavételez. A szinkronizálásból adódó problémák elkerülése érdekében a tényleges kiadott jel egy 100ms-os előszakasz és egy szintén 100ms-os utószakaszt is tartalmaz, amik alatt a felhasználó által definiált jel első, illetve utolsó feszültségértékét adja ki a mérőkártya. A függvény egyetlen paramétert vár, magát a kiadandó jelet, mely sor- vagy oszlopvektor formátumú kell legyen és a pontonkénti feszültséget tartalmazza Volt egységben. A maximális engedélyezett amplitúdó +-10V. A függvény kimenetként visszaadja (a felsorolás sorrendjében) az időalapot, a kimenetre küldött programozott jelet és a két bemeneti csatornán mért adatokat.
- A myDAQ_sin_rw függvénnyel egy 0.1Hz-50kHz frekvenciájú és 0.01-5V amplitúdójú megadott számú periódusból álló szinuszjelet tud a kártya "AO0" csatornáján kiadni, miközben az "AI0" és "AI1" csatornákon mintavétele. A függvény egy szoftveres triggerelést valósít meg (felmenő éra), melyhez egy 100ms-os előszakasz és egy szintén 100ms-os utószakasszal egészíti ki a felhasználó által definiált jelet. A függvény első bemeneti paramétere a szinuszjel frekvenciája Hz egységekben, második paramétere a periódusok száma, míg harmadik (opcionális) paramétere az amplitúdó (alapértelmezett értéke 1V). A függvény kimenetként visszaadja (a felsorolás sorrendjében) az időalapot, a kimenetre küldött programozott jelet és a két bemeneti csatornán mért adatokat.
BNC csatlakozós elektronikai dobozok
Az elektromos mérések során ún. BNC csatlakozós koaxiális kábeleket használ, melyek egy belső érből és egy külső palástból állnak. Ezeket a kábeleket a gyakorlatban kezelhetjük úgy, mint egy vezetékpárt. Az egyes áramköri elemek (ellenállások, kondenzátor, tekercs) fémbobozokban találhatók és a kivezetésük ún. szigeteletlen BNC csatlakozókkal került megoldásra. Ez azt jelenti, hogy a csatlakozó külső része, azaz a BNC kábel palástja (tehát a vezetékpár egyik vezetéke), elektromosan csatlakozik a fémdobozhoz, így a fémdoboz és minden dobozra csatlakoztatott BNC kábel külső palástja egy ekvipotenciális pontnak tekinthető (tipikusan földpont).
A mérőhelyen rendelkezésre áll egy olyan ellenállásdoboz, melyben több ellenállás található. Az ellenállások egyik lába egy közös kivezetésre, míg a másik láb ellenállásonkánt egy-egy saját kivezetésre van csatlakoztatva. Szintén rendelkezésre áll egy kondenzátort és egy tekercset tartalmazó doboz, amiben hasonló elven a két áramköri elem egy-egy saját kivezetés mellett osztozik egy közös kivezetésen. A lét doboz vázlata az alábbi ábrákon látható:
Könnyen belátható, hogy a fenti dobozokkal egy-egy áramköri elemre is tudunk csatlakozni (közös csatlakozó és az adott elem saját csatlakozója), de elő tudunk állítani soros és párhuzamos kapcsolásokat is.
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
FELADATOK ELSŐ ALKALOMMAL
A méréshez rendelkezésre álló eszközök
1. A rugóállandó mérése
Csavarja be az akasztószemet a rúd alján található menetbe, majd állítsa be a zsinór hosszát úgy, hogy a mérőrúd alja körülbelül a rúdvezető alsó széléhez essen! Akassza rá az egyik 25 g-os rézsúlyt egy kis kampó segítségével a mérőrúdra! Mérje le a rugó sztatikus megnyúlását! Ezután helyezzen fel egymás után több rézsúlyt is, és mérje meg az újabb megnyúlását! Ábrázolja az erő - megnyúlás grafikont és illesztéssel határozza meg a rugó rugóállandóját!
2. Csillapítatlan rendszer lengésideje
Szabályozza be a készüléket!
- Nagyon fontos, hogy a mérőrúd ne érjen a rúdvezető egyik falához se (lásd az előző pontban)!
Ehhez a méréshez szerelje le a csillapító mágnespofákat! Húzza a mérőrudat kb. 5 cm-rel az egyensúlyi helyzete alá, és engedje el! Indítsa el a Logger Lite programban a mintavételezést és rögzítsen legalább 5-10 periódust! Az "Export As" menüpontot használva mentse el az adatokat .txt formátumú fájlba és töltse be a Matlab-ba, majd határozza meg a rezgés periódusidejét. A mérést üres mérőrúddal, majd egy és két súly ráhelyezésével is végezze el!
- A súlyok (korongok) tömege 50g.
- A Logger Lite szoftver beállításához kérje a mérésvezető segítségét!
- A mért adatok Matlab-ba való betöltésére (és akár a görbeillesztésre) célszerű egy függvényt készítenie, mert a későbbi méréseknél szintén el kell végezni a betöltést és illesztést.
- Ha nehézséget okoz a beolvasó függvény elkészítése, itt talál hozzá segítséget. A szinuszjelek illesztésére és szolgáló függvényhez pedig itt talál segítséget.
- Az eredményeket foglalja táblázatba és vesse össze az elmélet alapján kiszámolt értékekkel!
3. Kényszerrezgés amplitúdójának és sebességamplitúdójának vizsgálata a kényszerítő frekvencia függvényében
A méréseket két különböző csillapítás esetén, mérőrúd + 50 g tömeggel végezze el! Szerelje vissza a csillapító mágnespofákat! A kis csillapításhoz a csillapító mágnespofákat egymástól kb. 2 cm-re állítsa be! A nagy csillapításhoz tekerje a mágnespofákat a lehető legközelebb, de csak annyira, hogy ne érjenek hozzá a csillapítórúdhoz! Ekkor mérje meg és jegyezze fel a mágnespofák távolságát!
Gondosan állítsa be a mérőrúd helyzetét, majd vizsgálja meg a csillapított szabad rezgést midkét csillapítás esetén! Ehhez térítse ki a mérőrudat kb. 5 cm-rel és vegye fel a mozását 60 s-ig.
Következő lépésként a motor feszültségének növelésével indítsa el a kényszerrezgést! A meghajtás elindítását célszerű kézzel segíteni, óvatosan lökje meg a meghajtókereket a nyíllal jelölt irányba. A mérés során lassan (fokozatosan) növelje a frekvenciát a feszültség növelésével, és keresse meg az 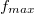 rezonanciafrekvenciát, ahol az amplitúdó maximális!
rezonanciafrekvenciát, ahol az amplitúdó maximális!
- NE HASZNÁLJON TÚL KICSI CSILLAPÍTÁST (túl távoli mágnespofák), mert a rezonanciafrekvencián az amplitúdó túl nagy lehet, ami károsíthatja a berendezést, vagy balesetet okozhat!
- A rezonanciafrekvencia – különösen nagy csillapítás esetében – eltér a sajátfrekvenciától.
- Amennyiben a rezgések amplitúdója túl nagy vagy túl kicsi lenne, úgy kapcsolja ki a készüléket és csökkentse, illetve növelje a kényszererő amplitúdóját, majd ellenőrizze a kitérést a rezonanciafrekvenciánál!
Amennyiben mindent rendben talál, végezze el újra a frekvencia hangolását és időről-időre álljon meg és várja meg az állandósult állapotot! A rezonanciafrekvenciánál 1 Hz-cel kisebb és 1 Hz-cel nagyobb frekvenciák közötti intervallumban mérjen kb. 0,1 Hz-enként (és a rezonancia frekvencia közelében ennél sűrűbben is)! Illesztéssel határozza meg az amplitúdókat és a frekvenciákat! Ábrázolja a különböző csillapítással felvett görbéket közös diagrammon! Adja meg minden esetben 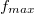 értékét!
értékét!
- Célszerű már a frekvencia hangolása közben elindítani a mintavételezést és a számítógépen figyelni mikor ér véget a tranziens viselkedés.
- Az adott frekvenciához tartozó állandósult állapotban történő méréshez indítson új mintavételezést és vegyen fel 10-20 periódust! Ennek a mérési fájlnak a automatizált betöltése és illesztáse egyszerűbb, mert nem szükséges az adatok levágása.
- Rögzítse a motor meghajtófeszültségének értékét is a különböző frekvenciáknál, a későbbi méréseknél segítségére lehet.
- Először végezze el a mérést nagyobb frekvencia lépésekben, majd ha szükséges, akkor finomítsa a felbontást!
A korábban megmért görbék valamennyi pontjánál (a kitérési amplitúdó és frekvencia ismeretében) számítsa ki a sebeségamplitúdó 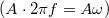 értékeket! Foglalja táblázatba és ábrázolja diagrammon a sebességamplitúdó – körfrekvencia görbéket!
értékeket! Foglalja táblázatba és ábrázolja diagrammon a sebességamplitúdó – körfrekvencia görbéket!
- A különböző csillapítással felvett görbéket most is közös diagrammon ábrázolja!
4. Csillapítási tényező és jósági tényező meghatározása
A csillapítási tényező kísérleti meghatározásának egyik lehetséges módszere a csillapodási hányados mérésén alapul, ehhez használja a 3. feladat csillapított szabad rezgésnél mért adatsorait! Ekkor egymás utáni lengések amplitúdócsökkenéseit mérjük.
Egy másik (esetenként előnyösebb) módszer a csillapítási- és jósági tényezők meghatározásra a sebességamplitúdó frekvenciafüggésének vizsgálata. Ehhez illesszen a 3. feladatban mért sebességamplitúdó adatokra a sebességamplitúdó – körfrekvencia függvénynek megfelelő görbét! Az illesztett görbe illesztési paraméterei között szerepel a  csillapítási tényező és az
csillapítási tényező és az  saját körfrekvencia (valamint az
saját körfrekvencia (valamint az 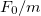 hányados). Az illesztés alapján határozza meg ezeket a paramétereket és hibájukat. Ezek alapján már meghatározható a jósági tényező is.
hányados). Az illesztés alapján határozza meg ezeket a paramétereket és hibájukat. Ezek alapján már meghatározható a jósági tényező is.
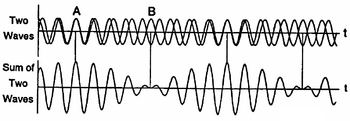
5. Szorgalmi feladat: Lebegés vizsgálata
Két, kis mértékben különböző frekvenciájú, szinuszhullám szuperpozíciójakor „lebegés” alakul ki (11. ábra). Ha 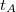 időpontban a rezgések éppen fázisban vannak, akkor a hullámok összeadódnak és az eredő rezgés maximális amplitúdójú lesz. Egy későbbi
időpontban a rezgések éppen fázisban vannak, akkor a hullámok összeadódnak és az eredő rezgés maximális amplitúdójú lesz. Egy későbbi 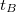 időpontban azonban a frekvencia különbség miatt a rezgések ellentétes fázisba kerülnek, és egymás hatását csökkentve minimális amplitúdót eredményeznek. Az amplitúdó változások burkológörbéje szintén szinuszos. A burkológörbe frekvenciája
időpontban azonban a frekvencia különbség miatt a rezgések ellentétes fázisba kerülnek, és egymás hatását csökkentve minimális amplitúdót eredményeznek. Az amplitúdó változások burkológörbéje szintén szinuszos. A burkológörbe frekvenciája 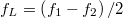 , ahol
, ahol 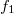 és
és 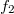 a két összetevő rezgés frekvenciája.
a két összetevő rezgés frekvenciája.
A kényszerrezgés bekapcsolásakor az állandósult tag mellett egy darabig megfigyelhető a csillapított rendszer idővel elhaló saját rezgése is. A differenciálegyenlet megoldása tartalmazza a bekapcsolás után kialakuló mindkét frekvenciát. A tranziens rezgés körfrekvenciája 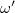 , az állandósulté pedig
, az állandósulté pedig  . Lebegés akkor figyelhető meg, ha a kényszererő
. Lebegés akkor figyelhető meg, ha a kényszererő  körfrekvenciája
körfrekvenciája 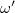 közelében van, és a csillapítás elég kicsi. Amint a tranziens elhal, a lebegés is megszűnik.
közelében van, és a csillapítás elég kicsi. Amint a tranziens elhal, a lebegés is megszűnik.
Szerelje le újra a csillapító mágnespofákat és állítsa be pontosan a mérőrúd helyzetét. Állítsa a kényszerkeréken az amplitúdót körülbelül 1-2 mm-re! Kapcsolja be a kényszermozgást és szabályozza annak frekvenciáját úgy, hogy körülbelül 0,1 Hz-cel legyen alacsonyabb, mint  és kapcsolja ki a kényszert! Várjon, amíg a mérőrúd megáll!
és kapcsolja ki a kényszert! Várjon, amíg a mérőrúd megáll!
Indítsa el az adatgyűjtést, majd kapcsolja be a kényszerrezgést! A lebegés megszűntéig mérjen!
Ábrázolja az amplitúdót az idő függvényében! Határozza meg a burkoló szinuszgörbe periódusidejét és frekvenciáját!
- Vesse össze az elmélet alapján várható értékekkel!
- Akkor kap szép lebegést, ha kicsi a csillapítás (leszedett mágnespofák, jól beállított mérőrúd (nem súrlódik).
- Vigyázzon, hogy leszedett mágnespofák mellett ne hangolja a kényszerrezgést a rendszer sajátfrekvenciájára, mert ekkor az amplitúdó jelentősen megnőhet!
FIGYELEM! A második alkalomra az eddigi feladatok előzetes kiértékelését el kell végezni és meg kell mutatni a mérésvezetőnek.
FELADATOK MÁSODIK ALKALOMMAL
Ha az előző alkalmon valamelyik feladatot nem sikerült befejeznie, vagy esetleg rossz eredményet kapott, akkor ismételje meg a mérést a gyakorlat végén!
- Általános megjegyzések:
- A méréshez egy National Instruments myDAQ mérőkártyát használunk egy saját készítésű panellel, melyre BNC csatlakozókkal köthetők be az egyes áramköri elemek!
- A különböző elemeket tartalmazó fémdobozokon ún. szigeteletlen BNC csatlakozók találhatók, ami azt jelenti, hogy a doboz maga is az áramkör része, ez a koaxiális BNC kábel külső "ere".
- Az váltóáramú mérési feladatok elvégzésekor azokban a frekvenciatartományokban, ahol jelentős a kimenő jel változása, sűrűbben vegyen fel mérési pontokat!
6. Egyszerű áramkörök egyenáramu jelének vizsgálata, ismerkedés a myDAQ kártyával és a BNC csatlakozókkal.
a) Egy ismert ellenállás felhasználásával állítson össze egy olyan kapcsolást, mellyel megmérhető egy áramköri elem 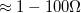 tartományba eső DC ellenállása az áram-feszültségkarakterisztika felvételével! Tesztelje az elrendezést egy-két ismert ellenállással!
tartományba eső DC ellenállása az áram-feszültségkarakterisztika felvételével! Tesztelje az elrendezést egy-két ismert ellenállással!
- A kapcsolás összeállításához használja a mérőhelyen található ellenállásdobozt!
- Az ellenállás megválasztásakor vegye figyelembe, hogy a myDAQ kártya kimenetén maximum
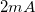 áramot tud kiadni!
áramot tud kiadni!
- Az I(V) karakterisztika felvételéhez a mérendő áramköri elemen eső feszültséget kell mermérni, az ismert ellenálláson eső feszültségből pedig meghatározható a körben folyó áram.
- Az I(V) karakterisztikát érdemes potitív és negatív tarományban is felvenni, az áramköri elem ellenállása a V-I grafikonra való egyenesillesztéssel kapható meg.
- A myDAQ_arb_rw függvény használatával adjon ki egy háromszögjelet és vegye fel az egyes elemeken eső feszültséget!
- Ideális esetben egy egyszerű ellenállás mérésekor a háromszögjel periódusidejétől nem függ a mért eredmény (ha nem lépjük túl a mérőeszköz határait), de egyéb áramköri elemek esetén ügyelni kell arra, hogy ne változtassuk túl gyorsan a feszültséget, mert különben nem tekinthető a kiadott jelünk egyenáramú jelnek.
b) Mérje meg a tekercs DC ellenállását!
- Végezze el a mérést néhány nagyságrendileg különböző frekvenciájú jellel is!
c) Egy ismert ellenállást és egy kondenzátort felhasználva állítson össze egy egyszerű RC kapcsolást. Hajtsa meg az RC kört egy 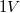 -os
-os 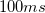 -os pulzussal és közben mérje meg a kondenzátoron eső feszültséget!
-os pulzussal és közben mérje meg a kondenzátoron eső feszültséget!
- Használja a mérőhelyen található ellenállásdobozt és a kondenzátort, valamint tekercset tartalmazó doboz megfelelő csatlakozóit!
- A pulzus kiadására használja a myDAQ_arb_rw függvényt!
- A kiadott jelet úgy szerkessze meg, hogy az
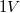 -os pulzus előtt legyen benen egy rövid
-os pulzus előtt legyen benen egy rövid 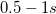 -os
-os 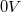 -os szakasz!
-os szakasz!
- A pulzus utáni
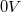 -os szakasz hosszát az ellenállás és a kapacitás névleges értéke alapján becsülje meg úgy, hogy legalább 6-10 időállandónyi legyen!
-os szakasz hosszát az ellenállás és a kapacitás névleges értéke alapján becsülje meg úgy, hogy legalább 6-10 időállandónyi legyen!
7. Szűrőkörök vizsgálata
a) Az előző feladatban vizsgált elrendezés egy aluláteresztő szűrőként funkcionál, mivel a kondenzátor impedanciája a frekvencia növekedésével csökken, ezért a rajta eső feszültség is csökken! Vizsgálja meg ezt a szűrőt! Ehhez hajtsa meg az RC kört különböző frekvenciájú ( ) szinuszjelekkel és mérje meg a (kondenzátoron eső) kimenő feszültséget! A bemeneti és a kimeneti szinuszjelet is mérje vissza, az amplitúdókat és a fázisokat illesztéssel határozza meg! Ábrázolja a
) szinuszjelekkel és mérje meg a (kondenzátoron eső) kimenő feszültséget! A bemeneti és a kimeneti szinuszjelet is mérje vissza, az amplitúdókat és a fázisokat illesztéssel határozza meg! Ábrázolja a 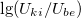 –
– 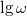 és a
és a 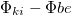 –
– 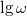 függvényt! Előbbire illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző
függvényt! Előbbire illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző 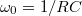 körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor (mért)
körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor (mért)  kapacitását! (
kapacitását! (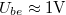 legyen!)
legyen!)
- A szinuszjel kiadásához használja a myDAQ_sin_rw függvényt!
Figyelem! A képletekből  -t számolunk, de a függvény paramétereként
-t számolunk, de a függvény paramétereként  -et kell megadni!
-et kell megadni!
- Készítsen egy olyan függvényt, mely automatikusan elvégzi a mérést és a mért szinuszjelek illesztését a megadott frekvenciatartományban a megadott lépésközzel! Ha nehézséget okoz a függvény elkészítése, akkor itt talál hozzá segítséget. A mérési naplóban egyértelműen jelezze, hogy saját, vagy az előre elkészített függvényt alkalmazza!
- A mérési naplóban írja le, hogy milyen elemeket használt fel a kapcsolás összeállításához! Válaszát számítással indokolja.
- Mivel az eredményeket logaritmikus skálán fogja ábrázolni, érdemes nagyjából logaritmikusan egyenletes sűrűséggel felvenni az adatokat. Pl.: 1 Hz, 2 Hz, 5 Hz, 10 Hz, 20 Hz, 50 Hz, 100 Hz, ...
- A maximális frekvencia megválasztásánál vegye figyelembe, hogy a mérőkártya mintavételezési frekvenciája
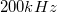 !
!
b) Az előző elrendezésben cserélje ki az ellenállást a már korábban is vizsgált tekercsre és az előző feladathoz hasonló módon vizsgálja meg az így összeállított LC szűrő!
- Vesse össze a két szűrő átviteli karakterisztikáját! Mi tapasztal?
8. Állítson össze párhuzamost LC rezgőkört!  külön elemként legyen bekötve, mert a kör áramát az ellenálláson eső feszültségből fogja meghatározni! A frekvencia függvényében mérje meg
külön elemként legyen bekötve, mert a kör áramát az ellenálláson eső feszültségből fogja meghatározni! A frekvencia függvényében mérje meg 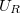 ,
, 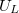 , és
, és 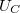 értékeit! Számítsa ki és ábrázolja a körben folyó
értékeit! Számítsa ki és ábrázolja a körben folyó  áramot és a
áramot és a 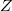 eredő impedanciát
eredő impedanciát  függvényében. A mért adatokra illesszen megfelelő függvényeket, és az illesztésből határozza meg
függvényében. A mért adatokra illesszen megfelelő függvényeket, és az illesztésből határozza meg  -t. Az eredmény (és a korábban megmért
-t. Az eredmény (és a korábban megmért  ,
, 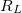 és
és  értékek) alapján határozza meg a tekercs
értékek) alapján határozza meg a tekercs  induktivitását!
induktivitását!
- Az illesztésnél vegye figyelembe a tekercs (korábban megmért) ohmos ellenállását is!
9. Állítson össze soros rezgőkört és vizsgálja meg az előző feladathoz hasonlóan!
- Melyik ellenállást célszerű választani az RLC-kör összeállításához, ha azt szeretné, hogy a rezonanciagörbe minél élesebb legyen? Válaszát indokolja!
- Az illesztésnél vegye figyelembe a tekercs (korábban megmért) ohmos ellenállását is!
10. Végezze el az előző mérést egy nagyobb sorba kötött ellenállással is! Végezze el most is az illesztést! Ábrázolja a két mérésnél kapott 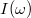 rezonanciagörbéket közös grafikonban!-->
rezonanciagörbéket közös grafikonban!-->
- Vesse össze a mért görbéket az első alkalommal mért mechanikai kényszerrezgések görbéivel! Mit tapasztal?
Vissza a Fizika laboratórium 2. tárgyoldalára.