Piezoelektromos állandók mérése
szerkeszt/-va/-ve/-ván/-vén alatt
A mérés célja:
- megismertetni a hallgatókat a piezoelektromos effektusokkal, a piezoelektromos állandók értelmezésével, illetve azok kísérleti meghatározási módszereivel.
A cél érdekében:
- értelmezzük a piezoelektromos állandókat,
- ismertetjük a kísérleti meghatározás lehetőségeit,
- ismertetjük a mérés során alkalmazott vizsgálati módszereket, a mérőkészülék felépítését és működését,
- megmérjük kerámia minták piezoelektromos állandóit.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Ha egy anyagot valamilyen külső hatás ér, akkor abban különböző változások jönnek létre, az anyag valamilyen módon „reagál” a külső hatásokra, amit megfigyelőként a hatástól függő jelenségként észlelünk. Mind az anyagot ért hatások, mind pedig az anyagban ilyenkor észlelhető jelenségek fizikai szempontból valamilyen fizikai mennyiséggel – illetve annak megváltozásával – jellemezhetők. Az, hogy meghatározott körülmények között egy hatás milyen erősségű változást (jelenséget) hoz létre, függ a vizsgált anyagtól, pontosabban az anyagnak az adott jelenség szempontjából fontos tulajdonságától.
Például: ha egy anyagot melegítünk, akkor az anyagot ért hatás a hőmérséklet változásával jellemezhető, a hőmérsékletváltozás által kiváltott egyik lehetséges jelenség pedig az, hogy megváltozik az anyag térfogata. Ugyanolyan hőmérsékletváltozás azonban különböző anyagokban különböző térfogatváltozást okoz, vagyis a jelenség „mértéke” az anyagi minőségtől függ és az anyag egy tulajdonságával – a térfogati hőtágulási együtthatóval – jellemezhető. Egy másikismert példa, hogy egy szigetelőanyag elektromos tér hatására polarizálódik. Itt a hatás az elektromos térerősség-vektorral, a jelenség a polarizáció-vertorral, a jelenségnek az anyagi minőségtől való függése pedig egy tenzorral, a dielektromos szuszceptibilitás tenzorával jellemezhető. Hasonlóan: egy test erőhatás következtében létrejövő alakváltozása esetén a hatás a feszültségtenzorral, a jelenség az alakváltozási tenzorral, az anyag tulajdonságai pedig a rugalmas együtthatókkal (amelyek ugyancsak tenzort alkotnak) jellemezhető.
A jelenségek számszerű leírásának alapvető feltétele az, hogy a vizsgált esetre vonatkozóan ismerjük a hatást, a jelenséget és a tulajdonságot jellemző fizikai mennyiségek közötti összefüggést. Szerencsére számos olyan jelenséget ismerünk amelynél – nem túl nagy hatások esetén – ez az összefüggés igen egyszerű formában írható fel. A pontos megfogalmazást egyelőre mellőzve, azt mondhatjuk, hogy a hatást és a jelenséget jellemző mennyiségek között egyfajta lineáris összefüggés áll fenn, amely szimbolikusan az alábbi alakban írhatunk fel:
![\[ \mbox{jelenség} = \mbox{tulajdonság}*\mbox{hatás} \]](/images/math/9/4/b/94bf79c538352fdcf88db52e9849d128.png)
Itt a „jelenség”, „tulajdonság”, „hatás” elnevezés fizikai mennyiségeket jelöl, amelyek matematikai szempontból skaláris- vektor- vagy tenzormennyiségek lehetnek. Ennek megfelelően a „  ” jel is különböző műveleteket jelenthet.
Az említet példák közül az állandó nyomás (P) mellett végbemenő hőtágulás esetében a hatás a
” jel is különböző műveleteket jelenthet.
Az említet példák közül az állandó nyomás (P) mellett végbemenő hőtágulás esetében a hatás a 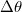 hőmérsékletváltozás, a jelenség a
hőmérsékletváltozás, a jelenség a 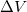 térfogatváltozás, a tulajdonság pedig az
térfogatváltozás, a tulajdonság pedig az 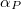 térfogati hőtágulási együttható. Az említett mennyiségek között az egyszerű
térfogati hőtágulási együttható. Az említett mennyiségek között az egyszerű
![\[ \Delta V = \alpha_P*\Delta\theta \]](/images/math/a/a/8/aa8cf10e17c0241010a33b715815e508.png)
tapasztalati összefüggés áll fenn (itt mindhárom mennyiség skalár). A másik példában a hatást jellemző E térerősség-vektor és a jelenséget jellemző P polarizáció-vektor kapcsolata – a vektorok derékszögű koordinátarendszerbeli komponenseit 1, 2, 3-mal jelölve – az alábbi lineáris egyenletekkel adható meg
![\[ \begin{array}{c} P_1 = \chi_{11}E_1+\chi_{12}E_2+\chi_{13}E_3 \\ P_2 = \chi_{21}E_1+\chi_{22}E_2+\chi_{23}E_3 \\ P_3 = \chi_{31}E_1+\chi_{32}E_2+\chi_{33}E_3 \end{array} \]](/images/math/9/b/2/9b23b3f01bd862fb21b882dfc4250896.png)
Az egyenletben szereplő 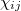 mennyiségek egy másodrendű tenzor komponensei, amelyet a
mennyiségek egy másodrendű tenzor komponensei, amelyet a
![\[ \chi = \left[ \begin{array}{lcr} \chi_{11} & \chi_{12} & \chi_{13}\\ \chi_{21} & \chi_{22} & \chi_{23}\\ \chi_{31} & \chi_{32} & \chi_{33} \end{array} \right] \]](/images/math/2/7/d/27dde165eaeec44badb2482d9adb413d.png)
szimbólummal jelölhetünk. Ezzel a jelöléssel a LINK (3) egyenleteket sűrített formában gyakran az alábbi módón írják fel:
![\[ \textbf{P} = \underline{\underline{\chi} } \cdot \textbf{E} \]](/images/math/9/a/d/9ade21dd110f6af15ee589290e8c30d3.png)
Ez az írásmód egy ilyen – másodrendű tenzort – tartalmazó egyenletnél még egyértelmű, magasabb rendű tenzorok esetén azonban nem derül ki belőle a szereplő tenzorok rendje, ezért helyette rendszerint az egyenleteket – bizonyos megállapodásokkal – rövidített indexes alakban használják. A LINK (3) egyenlet ilyen indexes alakja:
![\[ P_i = \chi_{ij} \cdot E_j \]](/images/math/1/b/d/1bd00a6dc9d8642732a88f4aa98ed202.png)
azzal a megállapodással, hogy az egyenletben ugyanazon tagban előforduló, megegyező indexekre (a LINK (6) egyenletben tehát j-re) összegezni kell, a magában álló index (i) helyébe pedig az 1, 2, vagy 3 érték helyettesítendő be ( így kapunk 3 egyenletet).
Ugyanilyen alakban írható fel a másodrendű tenzorral jellemezhető mechanikai feszültség (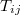 ) és a deformáció (
) és a deformáció (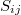 ) közötti kapcsolatot megadó általános Hooke-törvény is:
) közötti kapcsolatot megadó általános Hooke-törvény is:
![\[ T_{ij} = c_{ijkl} \cdot S_{kl} \]](/images/math/6/0/b/60b7e58ddd0a8516b8168f58ea5888f8.png)