Mágneses momentum mérése vibrációs magnetométerrel

A mérés célja:

A mérés célja megismerkedni egy makroszkopikus minta mágneses dipólmomentumának mérésével, valamint megvizsgálni egy lágymágneses anyag momentumának változását a külső mágnesező tér függvényében. A külső mágneses teret egyenáramú gerjesztő tekerccsel hozzuk létre, amely a különböző mintákban eltérő mágneses dipólmomentumot kelt. A mágneses térerősség mértéke a gerjesztő tekercs áramával szabályozható. Az ily módon felmágnesezett minta közelébe helyezett másik tekercsben (mérőtekercs) a dipólmomentum tere mágneses fluxust hoz létre. Ha a mintát a mérőtekercshez képest mozgatjuk, a tekercsben fluxusváltozás lép föl, ami feszültséget indukál. Az indukált feszültség értékéből a minta mágneses momentuma meghatározható. A mérési összeállítás akkor optimális, ha az elemek paramétereinek megválasztása révén (tekercsek alakja, minta helye stb.) a mért feszültség arányos a mágneses momentummal, valamint értéke a lehető legnagyobb.

Elméleti összefoglaló

Elméleti alapok

Egy H mágneses térerősségvektorral jellemzett térben lévő közegben kialakuló B mágneses indukció a következő összefüggéssel írható le:

 

$\[\mathbf{B} = \mathbf{\mu_0}(\mathbf{H} + \mathbf{M})\]$

(1)

ahol M a mágneses dipólmomentum sűrűség vektor vagy mágnesezettségi vektor. Egy makroszkópikus méretű, „V” térfogatú test mágneses momentuma (m) a következő térfogati integrálással kapható meg:

 

$\[\mathbf{m} = \mathbf{\int \limits_V M} dV\]$

(2)

A mérés során az m(H) függvényt szeretnénk meghatározni. A mérés a mágneses indukció jelenségén alapul, vagyis mindenekelőtt meg kell határoznunk a bevezetőben említett mérőtekercsben indukált „U” feszültség és az m mágneses momentum közötti kapcsolatot. Az alábbiakban kivonatosan bemutatjuk a keresett összefüggés levezetését. Kiindulásul a Maxwell-egyenleteket alkalmazzuk kvázistacionárius közelítésben, azaz az időben változó terek okozta sugárzást elhanyagoljuk. A levezetés kulcsgondolata szerint először összehasonlítjuk egy „I” áramjárta tekercs mágneses terébe helyezett m mágneses dipólus energiáját azzal az energiával, amit ugyanez a dipólus tárol ugyanebben a tekercsben az általa létrehozott 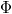$\setbox0\hbox{$\Phi$}% \message{//depth:\the\dp0//}% \box0%$ fluxus által. Így megkapjuk a 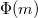$\setbox0\hbox{$\Phi(m)$}% \message{//depth:\the\dp0//}% \box0%$ összefüggést. Mivel a fluxusnál az indukált feszültség sokkal egyszerűbben mérhető, mozgatni fogjuk a mintát, és meghatározzuk a keresett U(m) összefüggést.

A mérés elve

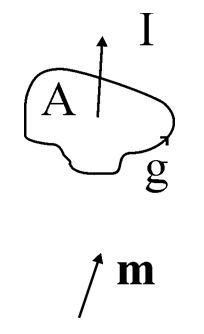
Először egy külső H mágneses térben lévő m dipólus energiáját (W₁) írjuk föl skalárszorzat formájában:

 

$\[W_1 = -\mathbf{m \cdot H}\]$

(3)

amelynek alakja abból adódik, hogy a mágneses tér a momentumra forgatónyomatékot gyakorolhat. Tegyük fel, hogy a mágneses teret egy „g” görbével jellemezhető hurokban folyó „I” áram határozza meg. Egy vákuumban lévő 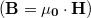$\setbox0\hbox{$(\mathbf{B = \mu_0 \cdot H})$}% \message{//depth:\the\dp0//}% \box0%$ hurok által keltett tér a Biot-Savart-törvény szerint:

 

$\[\mathbf{H(r)} = I \cdot \oint_g \frac{d\mathbf{r'}\times{}\left(\mathbf{r-r'}\right)}{{\left\vert{}\mathbf{r-r'}\right\vert{}}^3} = I \cdot \mathbf{H^e}\]$

(4)

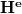ahol $\setbox0\hbox{$\mathbf{H^e}$}% \message{//depth:\the\dp0//}% \box0%$-vel jelöltük az egységnyi áram által keltett mágneses térerősséget, amely csupán a geometriától függ. Ezt behelyettesítve (3)-ba a következőt kapjuk:

 

$\[W_1 = - \mathbf{m} \cdot \mathbf{H^e} \cdot I\]$

(5)

Másodszor azt nézzük meg, hogy mekkora az energiája az m mágneses momentum keltette B mágneses indukciójú térben található „A” felületű vezető huroknak, melyben „I” áram folyik:

 

$\[W_2 = \frac {I \cdot \Phi} {2} \]$

(6)

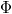ahol $\setbox0\hbox{$\Phi$}% \message{//depth:\the\dp0//}% \box0%$ a hurokban fellépő mágneses indukciófluxus:

 

$\[\Phi = \int_A \mathbf{B} d\mathbf{A}\]$

(7)

1. ábra. A mágneses momentum és a mérőhurok.

Amennyiben az „I” árammal H térerősséget létrehozó, valamint a Φ fluxust tartalmazó hurok és a mágneses momentum egy és ugyanaz mind a két esetben, az előbbi energiakifejezéseknek egyenlőnek kell lenniük:

 

$\[W_1 = W_2 \qquad \to \qquad -\mathbf{m} \cdot \mathbf{H}^e \cdot I = \frac{I\cdot \Phi}{2}\]$

(8)

ahol I-vel egyszerűsíthetünk, így a mágneses fluxus a hurokban:

 

$\[\Phi = - 2\cdot \mathbf{m} \cdot \mathbf{H}^e\]$

(9)

Most azt az esetet vizsgáljuk meg, amikor a mágneses dipólust mozgatjuk a mérőhurokhoz képest. Ekkor a geometria változása fluxusváltozást eredményez, amely a mérőtekercsben indukált feszültséget (U) hoz létre:

 

$\[U(t) = - \frac{d \Phi }{dt} = -\frac{d \Phi }{d \mathbf{r} } \cdot \frac{d \mathbf{r} }{dt} = -2 \cdot grad \left(\mathbf{m} \cdot \mathbf{H} ^e\right) \cdot \frac{d \mathbf{r} }{dt}\]$

(10)

A fenti összefüggésben az idő (t) szerinti deriválást a láncszabály alapján mindjárt átalakítottuk hely szerinti deriválásra, ahol r a dipólus helyvektorát jelenti. Az m a végső mérendő mennyiség, értékét a gerjesztő tekercs árama határozza meg, ami egy mérési pontban időben állandó. Ha a dipólus mozgástartománya kicsi a gerjesztő tekercs jellemző méreteihez képest, m értéke a mozgás során helyfüggetlen is, mivel kis helyváltoztatás során a gerjesztő tekercs mágneses tere állandó. A mágneses momentum épp ezért kiemelhető a gradiensből, ahol így csak H^e marad. Ha a mérési elrendezés geometriája olyan, hogy H^e-nek, m-nek és a helyvektor dr megváltozásának csak azonos irányú komponense van, és a koordináta rendszerünket úgy vesszük fel, hogy a z-tengelye ebbe az irányba mutat, akkor a fenti mennyiségek helyettesíthetők H_z^e, m_z ill. dz komponenseikkel. Ekkor a fenti kifejezés a következőre egyszerűsödik:

 

$\[U(t) = -2\cdot m_z \cdot \frac{\partial H_z^e}{\partial z}\cdot \frac{dz}{dt}\]$

(11)

A dipólus mozgatása során fellépő indukált feszültség tehát akkor mérhető könnyen, ha időben vagy állandó, vagy harmonikusan változik. Az előbbihez a dipólus egyenes vonalú egyenletes mozgását kellene biztosítani a helytől lineárisan függő H_z^e esetén, ami nehezen kivitelezhető. Kézenfekvő tehát a dipólus „z₀” amplitudójú, ω körfrekvenciájú szinuszos rezgetése. Ekkor a fenti összefüggés a következő alakot ölti:

 

$\[U(t) = -2\cdot m_z \cdot \frac{\partial H_z^e}{\partial z}\cdot z_0\cdot \omega \cos(\omega t)\]$

(12)

Látható, hogy a legnagyobb indukált feszültséget akkor kapjuk, ha a minta mozgása gyors, valamint ha az egységnyi áram által keltetett mágneses tér gyorsan változik a hellyel. Ebben az esetben akkor lesz az indukált feszültség arányos m-el, ha H_z^e hely szerinti változása a mozgás tartományában első rendben állandó, azaz 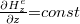$\setbox0\hbox{$\frac{\partial H_z^e}{\partial z} {{=}} const$}% \message{//depth:\the\dp0//}% \box0%$. A feladat tehát egy ilyen mérőhurok geometriát találni.

2. ábra. A mérőhurok geometriája a magnetométerben.

A vibrációs magnetométer

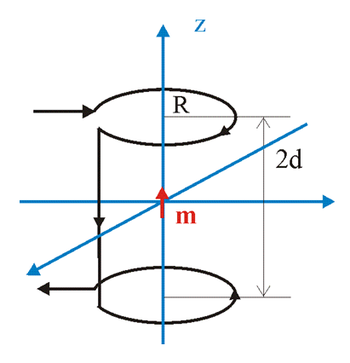
A Biot-Savart törvény itt nem részletezett alkalmazásával meg lehet győződni róla, hogy a 2. ábrán látható kettős mérőhurok elrendezés alkalmas a 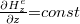$\setbox0\hbox{$\frac{\partial H_z^e}{\partial z} {{=}} const$}% \message{//depth:\the\dp0//}% \box0%$. feltételnek megfelelő mágneses tér előállítására, és ne felejtsük el, hogy így az induktivitás kölcsönössége, azaz az ekvivalenciánk alapján ideális mérőhuroknak/-tekercsnek is. A levezetésben csak a két ellentétes körüljárású áramhurok terének z komponensét kell meghatározni a z tengely mentén, majd annak megfelelő deriváltját képezni. Ez a z = 0 „középpontban” és annak z << d kis környezetében az ábra jelöléseit felhasználva az alábbi alakot ölti:

 

$\[\frac{\partial H_z^e}{\partial z} = - \frac{3 \cdot R^2 \cdot d}{\left( R^2+d^2\right) ^{5/2} }\]$

(13)

amely valóban állandó (z-től független). Maximális értékét megfelelő R/d arány mellett veszi fel, melyet az R = áll. feltételes szélsőérték keresésével határozhatunk meg. Ennek eredménye:

 

$\[\frac{\partial}{\partial d}\cdot \frac{\partial H_z^e}{\partial z} = \left( R^2 + d^2 \right)^{5/2} - 5 \cdot \left( R^2 + d^2 \right)^{3/2} \cdot d^2 = 0 \qquad \Rightarrow \qquad R = 2d\]$

(14)

vagyis az R sugarú hurkokat úgy kell elhelyezni, hogy éppen R távolságra legyenek egymástól. Ha a hurkok helyett N menetes tekercseket alkalmazunk, az indukált feszültség (12)-ben megadott értékének is N-szeresét kapjuk:

 

$\[U(t) = 2\cdot N\cdot m_z \cdot \frac{12}{5^{5/2}\cdot d^2} \cdot z_0 \cdot \omega \cos(\omega t)\]$

(15)

3. ábra. A mérési elrendezés vázlatrajza.

4. ábra. A mérőkészülék a valóságban.

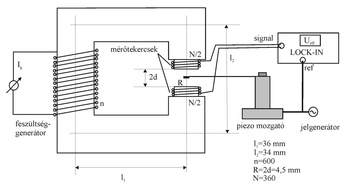
Nem esett még szó a minta felmágnesezéséről, melyhez egy megfelelő erősségű homogén mágneses térre van szükség. Erre a célra alkalmas a 3. ábrán és a 4. fényképen is látható lágyvas maggal/járommal ellátott elektromágnes, melyet egyik oldalán egyenárammal (Ig) táplált „n” menetű tekercselés vesz körül. A másik oldalon a résben közelítőleg homogén tér alakul ki, amely a rés közepén, ahová a mintát is helyezzük még inkább megfelel ennek a feltételnek. A 3. ábrán az is látható, hogy szintén a rés két oldalára került a két mérőtekercselés. Végeredményben egyfajta „transzformátort” kaptunk, melyben nem a primer köri áram váltakozik az idővel, hanem a tekercsek közti induktív csatolást erősítő kétrészes vasmag (nagy lágyvas tömb és a kisméretű minta). A résben keltett mágneses tér közelítő meghatározásához a gerjesztési törvényt alkalmazzuk. Az ábra jelöléseit használva:

 

$\[\mathbf{\oint H dr} = \sum I \qquad \Leftrightarrow \qquad H_{Fe} \cdot 2I_1 + H_{Fe} \cdot (2I_2 - 2d) + H_{r\acute{e}s} \cdot 2d = n \cdot I_g\]$

(16)

A rés és vasmag határán (izotróp permeabilitású vasmagot feltételezve, ahol B és H párhuzamos) a tér jó közelítéssel a határfelületre merőleges irányú, tehát a B indukció megy át folytonosan: 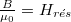$\setbox0\hbox{$\frac{B}{\mu_0} = H_{r\acute{e}s}$}% \message{//depth:\the\dp0//}% \box0%$ valamint 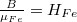$\setbox0\hbox{$\frac{B}{\mu_{Fe}} = H_{Fe}$}% \message{//depth:\the\dp0//}% \box0%$. Behelyettesítve (16)-ba adódik:

 

$\[B = \frac{n\cdot \frac{I_g}{2} }{\frac{I_1 + I_2 + d}{\mu_{Fe} }+\frac{d}{\mu_0} }\]$

(17)

Itt a nevezőben az első tag a µ_Fe nagyon nagy értéke miatt elhanyagolható a második tag mellett, így:

 

$\[B \approx \frac{\mu_0\cdot n\cdot I_g}{2\cdot d}\]$

(18)

valamint a térerősség a légrésben

 

$\[H_{r\acute{e}s} \approx \frac{n\cdot I_g}{2d}\]$

(19)

A mérőkészülék további részei: a mágnesező tekercs táplálását egy feszültséggenerátor biztosítja, a mintát pedig egy piezoelektromos mozgató rezgeti, melyet egy jelgenerátor szinuszos jelével hajtunk meg. Az indukált feszültség mérésére annak kis értéke és a zajok kiküszöbölése érdekében egy fázisérzékeny lock-in erősítőt használunk (ld. fázisérzékeny detektálás), mely az 5. fényképen látható. Ennek működési elve a „Kis fényintenzitások mérése zajos környezetben: Fázisérzékeny detektálás(lock-in)” c. hallgatói mérésben megtalálható, azonban ismerete jelen mérésnél nem szükséges. Jelenleg annyit elég tudnunk, hogy a műszer a mérendő szinuszos jel effektív értékét határozza meg és jelzi ki, azaz (15) alapján:

 

$\[U_{eff} = 2N\cdot m_z\frac{12}{\sqrt{2}\cdot 5^{5/2}\cdot d^2}\cdot z_0\cdot \omega\]$

(20)

5. ábra. A fázisérzékeny (lock-in) erősítő.

Mérési feladatok

A feladat két különböző anyagú minta vizsgálata, és mágneses momentumaik arányának meghatározása. Ehhez a mágnesező áram függvényében az indukált feszültséget mérjük különböző értékeknél. Mivel a gerjesztő áram (I_g) a mágnesező térrel (H_rés) arányos, a mért indukált feszültség (U_eff) pedig a tér által okozott mágnesezettséggel/mágneses momentummal (m_z), a felvett U_eff - I_g görbék mágnesezési görbének is tekinthetők.

• 1. feladat

Helyezze az 1-es számmal jelzett mintát a mágnespofák közé! Ehhez a készüléken lévő fehér gombot le kell nyomni és elforgatni, hogy úgy maradjon (retesz). A mintát a tartójával úgy kell elhelyezni, hogy a minta a pofák között pontosan középen legyen. A mintatartót ütköztesse a gomb alsó szárához majd rögzítse azt! Ezután felengedheti a gombot. A piezoelektromos mozgatót meghajtó szinuszos jel amplitúdója legyen 1V pp (csúcstól csúcsig). Ezt az oszcilloszkópon ellenőrizheti.

Csatlakoztassa a mérőtekercs kimenetét a lock-in erősítő jelbemenetéhez (Signal A), valamint a jelgenerátor kettéosztott jelét a piezo mozgatóhoz és a lock-in erősítő referencia bemenetéhez (Reference input). Kapcsolja be az erősítőt, és helyezze a legérzéketlenebb állásba (Sensitivity 1000 mV)! Állítsa a referencia kijelzőt Freq-re, valamint az időállandót (Time constant) 100 ms állásba. A feszültség kijelző rész legyen Signal in állásban. Állítsa be a jelgenerátor frekvenciáját 1500±50 Hz-re. Ezt az értéket a lock-in erősítőn tudja pontosan ellenőrizni.

Az egyenáramú tápegységen a bal oldali áramérték kijelző alapján állítson be 1 A gerjesztő tekercs áramot a feszültségváltoztató potméterekkel! Nyomja meg a lock-in erősítő AUTO gombját, és várjon, amíg a felette lévő LED kialszik! Ekkor az erősítő a mért és a referencia jelet azonos fázisba hozta. Ha a beállás során megváltozott az időállandó, állítsa vissza az eredeti értékekre. Ha szükséges, manuálisan keresse meg azt az érzékenységet (Sensitivity), amelybe a mért jel még éppen belefér, majd az áramot csökkentse 0 A-re, és nyomja meg az erősítőn az AUTO ZERO gombot (ha szükséges, többször is)!

Ekkor az elrendezés készen áll a mérésre. Vegye fel a minta U_eff-I_g görbéjét 0,1 A-es lépésekben a következők szerint: először 0-tól 1 A-ig, majd vissza −1 A-ig (0-nál pólusváltás szükséges a banándugókkal), végül vissza 0 A-ig.

• 2. feladat

Ismételje meg az első feladat lépéseit a 2-es számú mintával.

Kiértékelés, jegyzőkönyv

Ábrázolja a kapott eredményeket U_eff - I_g diagramon! Értelmezze a látottakat! Ábrázolja az azonos áramértékekhez tartozó feszültségeket U_eff,1-U_eff,2 diagramon. A megfelelő szakaszra történő egyenes-illesztéssel határozza meg a mágneses momentumok arányát! Mekkora a mágnesező tér legnagyobb értéke?

PDF formátum

Mágneses momentum mérése vibrációs magnetométerrel (nem korrigált változat)