Méréstechnika szerkesztőlap
Tartalomjegyzék |
Spektrumanalízis
Egy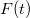 
időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg:
![\[f(\omega)=\int_{-\infty}^{\infty} F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t.\]](/images/math/5/9/5/595ba94d38747532dc0a86ce5c451009.png)
Egy valós mérésnél a Fourier-transzformált függvényt csak közelítőleg tudjuk megadni, hiszen egyrészt véges ideig tart a mérésünk, másrészt a mérési adatok csak diszkrét időfelbontással álnak rendelkezésre. Először nézzük meg a véges idejű mérés hatását a Fourier-transzformáltra.
A véges idejű mérés megfelel annak, mintha az eredeti függvényt megszoroznánk a mérési intervallumnak megfelelő 
ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki:
![\[f_W(\omega)=\int_{-\infty}^{\infty} W(t)\cdot F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t,\]](/images/math/8/3/d/83d2a1130cc875baedfb60e75dbff165.png)
ahol a függvény 
esetén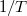 
, ezen 
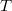hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz:
![\[ f_W(\omega)=\int_{-\infty}^{\infty} f(\omega ')w(\omega - \omega ')\frac{\mathrm{d}\omega}{2\pi},\ \ \ \ \mathrm{ahol}\ \ \ w(\omega)=\int_{-\infty}^{\infty} W(t)\mathrm{e}^{-i\omega t}\mathrm{d}t. \]](/images/math/0/5/8/0582a6df73925371593d682d300af119.png)
Nézzünk egy egyszerű példát, legyen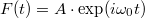 
egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény: 
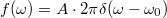. Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján 
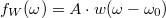, azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az 
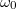középfrekvenciához eltolva. A fent definiált téglalap ablak esetén (azaz amikor egy 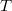szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja 
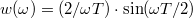, azaz 
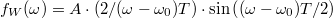(5b. ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az 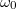középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az 
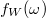függvény 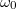melletti első zérushelyeinek a távolsága 
, így az 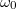körüli csúcs szélessége 
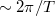. Tehát az első fontos konklúzió, hogy véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg 
frekvenciafelbontással látjuk!
 |
| 5. ábra. a) ablakfüggvény téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. b) 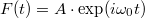harmonikus jel Fourier-transzformáltjának abszolút érték négyzete téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. A téglalap ablakot Hanning ablakra cserélve az 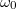körüli csúcs kiszélesedik, azaz romlik a frekvenciafelbontás, azonban az 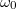-tól távolabbi mellékcsúcsok amplitúdója lecsökken, azaz csökken a spektrális szivárgás.
|
Érdemes megjegyezni, hogy a fent említett téglalap ablak helyett választhatunk más ablakfüggvényt is, például 
ún. Hanning-ablak esetén a mért jelben elnyomjuk a mintavételezési időablak széleihez közeli részeket (5a. ábra, piros szaggatott vonal). Ebben az esetben az 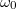körfrekvenciás jel Fourier-transzformáltjában 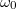körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az 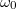-tól távolabbi oszcillációk amplitúdója (az ún. spektrális szivárgás) lecsökken (5b. ábra, piros szaggatott vonal).
Következő lépésként nézzük meg, hogy mi a hatása annak, hogy a jelünket nem folytonosan látjuk, hanem csak diszkrét mintavételezési időpontokban. Emiatt a jel Fourier-transzformáltját a folytonos integrál helyett kénytelenek vagyunk egy diszkrét összeggel, az ún. diszkrét Fourier-transzformálttal (DFT) közelíteni:
![\[ f_W(\omega)=\sum_{n=0}^{N-1} W(n\cdot \Delta t)F(n\cdot \Delta t) \mathrm{e}^{-i\omega n \Delta t}\Delta t, \]](/images/math/1/c/2/1c29d0a765e68527b917bd9e7cc0b666.png)
ahol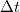 
a szomszédos mérési pontok közötti idő, 
pedig a mintavételezett pontok száma.
Az ún. Nyquist-Shannon mintavételezési törvény szerint 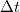sűrűségű mintavételezés esetén a jelet 
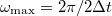maximális körfrekvenciáig tudjuk rekonstruálni.
Könnyen belátható, hogy a diszkrét Fourier-transzformált fenti képlet szerinti kiértékelése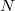 
mérési pont esetén 
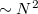művelet (
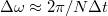frekvenciafelbontás és 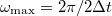maximális felbontható frekvencia esetén csak 
diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián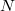 
művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa (
), és a frekvenciatérben 
diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma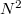 
-ről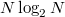 
-re csökken, ami nagy N esetén lényeges különbség.
A mérőműszerek jelentős része, így a laborgyakorlaton használt digitális oszcilloszkóp is az FFT algoritmus numerikus kiértékelése alapján határozza meg a mért jel spektrumát. A legtöbb esetben a műszer nem adja meg külön a spektrum valós és képzetes részét, hanem csak a Fourier-transzformált abszolút érték négyzetét látjuk. Ezen kívül a mérőműszerek általában a frekvencia, és nem a körfrekvencia függvényében adják meg a spektrumot, erre érdemes odafigyelni a mérés kiértékelésénél.
A Fourier-transzformáció nem csak a jel frekvenciájának a vizsgálatára alkalmas, hanem a jel amplitúdójának a mérésére is. A fenti képletek szerint egy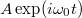 
harmonikus jel téglalap ablakkal vett Fourier transzformáltja az 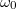körfrekvenciánál pontosan 
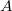amplitudóval rendelkezik. Az 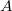amplitúdót azonban csak akkor kapjuk vissza, ha a jel körfrekvenciája megegyezik az FFT valamelyik frekvenciapontjával (
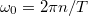), ami akkor teljesül, ha a jelnek pontosan egész számú periódusa fér el a 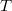mintavételezési ablakban. (Érdemes megjegyezni, hogy ebben az esetben az FFT összes többi frekvenciapontja a téglalapablakkal számolt Fourier-transzformált zérushelyeivel esik egybe, azaz a spektrális szivárgás is megszűnik.) Azonban ha a mérési ablak szélessége nem egyezik meg a jel periódusidejének egész számú többszörösével, akkor az FFT-algoritmus által számolt frekvenciapontok biztosan eltérnek a mért jelünk frekvenciájától, így az amplitúdóra is pontatlan értéket kapunk. Ha a jel amplitúdója érdekel minket, akkor olyan ablakfüggvényt érdemes választni, melynek a Fourier-transzormáltja a centrális csúcs körüli 
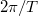szélességű tartományban minél kevesebbet változik. Téglalapablak esetén az amplitúdópontosság mintegy 36%, Hanning-ablak esetén pedig 15%. Speciális, ún. Flattop-ablakot választva ennél sokkal jobb, mintegy 0.01%-os amplitúdópontosság is elérhető, viszont cserébe lényegesen leromlik a frekvenciafelbontásunk.
A zaj
A zaj definíciója
Egy 
időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy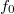 
középfrekvencia körüli 
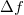szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány 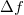szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectral Density - PSD):
![\[\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.\]](/images/math/f/c/e/fcef50d6c156742a0f491cc490623688.png)
Ez a zaj kísérleti definíciója. A feszültség szórásnégyzete a zajsűrűség teljes frekvenciatartományra vett integráljával egyenlő.
![\[\langle(\Delta V(t))^2 \rangle=\int_{0}^{\infty} df s_V(f).\]](/images/math/4/e/5/4e5f54e003163e2b26ac0e5c132ede8d.png)
Ez a képlet közvetlenül is használható a zajspektrum kísérleti meghatározásához, azonban emellett jó kiindulópontként szolgál más fizikai mennyiségekkel való kapcsolatának vizsgálatára is. Érdemes megvizsgálni a zajsűrűség és a feszültség korrelációs függvény kapcsolatát. Ez utóbbi a következőképpen definiálható:
![\[C(\Delta t)=\langle\Delta V(t)\cdotp\Delta V(t+\Delta t) \rangle=\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T}dt\Delta V(t)\cdotp\Delta V(t+\Delta t).\]](/images/math/2/2/4/2249b4df683368d4b8351cadfb3df188.png)
Könnyen belátható, hogy a korrelációs függvény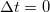 
-ban megegyezik a feszültség szórásnégyzetével.
![\[C(0)=\langle(\Delta V(t))^2 \rangle.\]](/images/math/a/b/5/ab573547effc08d355afcf78edbf2b69.png)
Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével:
![\[C(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{i\omega t}c(\omega).\]](/images/math/9/2/d/92d0898595e749cda299df5939826fab.png)
Ez alapján a feszültség szórásnégyzete:
![\[\langle(\Delta V(t))^2 \rangle=C(0)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega c(\omega)=\frac{1}{\pi}\int_{0}^{\infty}d\omega c(\omega),\]](/images/math/1/e/f/1eff86c194f06c16f8941773197552b2.png)
mivel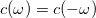 
.
Másrészt a szórásnégyzet és a zaj közötti összefüggésből következik:
![\[\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).\]](/images/math/7/9/7/7975f3b4b9d91fc7591790411d47208e.png)
Az utóbbi két egyenletből látható, hogy a zaj teljesítménysűrűsége a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
Sikerült kapcsolatot teremteni a zajsűrűség és a feszültség korrelációs függvény között. Most vizsgáljuk meg a feszültség korrelációs függvény és a feszültség mint mérhető fizikai mennyiségek kapcsolatát. A feszültség átlagtól való eltérésének (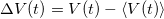
) a Fourier-transzformáltja szerint:
![\[\Delta v(\omega)= \int_{-\infty}^{\infty} dt \Delta V(t)e^{-i\omega t}.\]](/images/math/2/9/6/2965fd4ba4a7bbef8a3053293de74505.png)
Vizsgáljuk ezen Fourier-transzformált abszolút érték négyzetének várható értékét:
![\[\langle|(\Delta v(\omega))|^2 \rangle= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} dt' dt \langle\Delta V(t)\Delta V(t') \rangle e^{-i\omega t} e^{i\omega t'}.\]](/images/math/4/c/e/4ce29a8e2825fd676032ef5e4d3274cb.png)
Az egyenlet jobb oldalán látható korrelációs függvény kifejezhető a következőképpen:
![\[ \langle\Delta V(t)\Delta V(t')\rangle=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega'c(\omega')e^{i\omega'(t-t')}.\]](/images/math/0/2/0/020ed4a8570c778e72bfcb56197a4710.png)
Továbbá az exponenciális tagokat átcsoportosítva a következő tag integrálja egy Dirac-deltát ad:
![\[\int_{-\infty}^{\infty}dt'\frac{e^{i(\omega+\omega')t'}}{2\pi}=\delta(\omega+\omega').\]](/images/math/0/9/5/095ca08f79957cdab9fa2f6b7d38b462.png)
Így a feszültség Fourier-transzformált abszolút érték négyzetének várható értéke könnyen belátható, hogy arányos a korrelációs függvény Fourier-transzformáltjával, illetve az időablak szélességével:
![\[\langle|(\Delta v(\omega))|^2 \rangle= c(\omega) \int_{-\infty}^{\infty} dt.\]](/images/math/b/e/7/be72f26b149e5ab64d53d20f46b4bc31.png)
Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
![\[s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle |\int_{-T/2}^{T/2} dt \Delta V(t)e^{-i\omega t}|^2\right\rangle.\]](/images/math/f/6/2/f62535c4ffea081a318dd4bd7ac2a654.png)
A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki:
![\[s_V(\omega)\approx\frac{2}{N\Delta t}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2=\frac{2\Delta t}{N}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/6/0/3/603ab5b3fd96cfbcbb85edb29268c6af.png)
A fentiekben sikerült megállapítanunk, hogy a vizsgált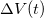 
jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk.
Nézzük meg, hogy egy tetszőleges ablakfüggvény esetén hogyan származtatható a zajsűrűség. Sajnos tetszőleges spektrumú zajra és tetszőleges ablakfüggvényre általános összefüggés nem adható, viszont ha 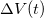fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor.
Az ablakfüggvénnyel szorzott jel Fourier-transzformáltja:
![\[\Delta v_W(\omega)=\int_{-\infty}^{\infty}dt\Delta V(t)W(t)e^{-i\omega t}.\]](/images/math/7/e/f/7efc09e6fe1e8b10c418e39ae67c31c9.png)
Vizsgáljuk meg ezen Fourier-transzformált abszolút érték négyzetének várható értékét, ekkor a következőt kapjuk:
![\[\langle|\Delta v(\omega)|^2\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dtdt'W(t)W(t')\langle\Delta V(t)\Delta V(t')\rangle e^{-i\omega t}e^{-i\omega t'}.\]](/images/math/7/d/3/7d3c7333af2e34f077367ef15237c488.png)
A fehér zaj jellegéből következik, hogy:
![\[\langle\Delta V(t)\Delta V(t')\rangle=C(t-t')=\frac{s_0}{2}\delta(t-t').\]](/images/math/7/2/c/72c3ab5d9e5160ea1cc93ce4aa1e97ae.png)
Így a Fourier-transzformált abszolút érték négyzetének várható értéke a következőképpen egyszerűsödik:
![\[\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.\]](/images/math/6/3/5/6356a96296e2b3eca8d114d91dae4d48.png)
Azaz a zajsűrűség számolása:
![\[s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.\]](/images/math/9/1/7/917c7b49524f91ef5d3aee98385f13b5.png)
A feszültségzaj spektrális sűrűsége egy normálási faktor erejéig egyenlő a mért feszültségpontok diszkrét Fourier-transzformáltjának abszolútérték-négyzetének kétszeresével. A normálási faktor az ablakfüggvény négyzetének a mérési időablakra vett integrálja. Láttuk, hogy ez téglalap ablakkal számolva . Most vizsgáljuk meg a zajméréshez leggyakrabban használt Hanning-ablakot, melynek ablakfüggvénye:
![\[W(t)=2\sin^2\left(\frac{t\pi}{T}\right).\]](/images/math/d/5/8/d58104d67248c78d0d25e0feb8d3b3ac.png)
A zajsűrűség Hanning-ablakot használva:
![\[s_0=\frac{4\langle|v_W(\omega)|^2\rangle}{3T}.\]](/images/math/b/d/e/bdee8db481fad34233895abf370d61ae.png)
Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés:
![\[s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}|\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.\]](/images/math/c/7/9/c798b690d1d9023a3a2741285d12ca1c.png)
Hanning-ablakkal számolva:
![\[s_0\approx\frac{4\Delta t}{3N}|\sum_{n=0}^{N-1}W(n\Delta t)\Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/e/1/1/e11505f5d483e5c169ac48ae35cc33ba.png)
Így frekvenciafüggetlen zajsűrűségek esetén sikerült analitikusan meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége.
Termikus zaj
Egy kristályban lévő elektronok termikus fluktuációi miatt külső feszültség nélkül az áram időátlaga nulla, azonban az adott időpillanatokban véletlen irányokba mutató áramokból áramfluktuációk alakulnak ki.
Ezt, az elektronok termikus fluktuációjából adódó zajt nevezzük termikus zajnak. Jellegét tekintve ez a zaj egy fehér zaj, azaz a zajsűrűsége független a frekvenciától.
A Drude-modell értelmében az elektronok elektromos tér által nyert impulzusát a kristályráccsal történő ütközése (szóródás, rácsrezgés keltése) során veszíti el. A modell értelmében a fajlagos vezetőképesség (
) arányos az elektronok átlagos sűrűségével (
), töltésük négyzetével (
) és az átlagosan két ütközés között eltelt idővel (
), továbbá fordítottan arányos az elektron tömegével (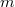
):
![\[\sigma=\frac{ne^2\tau}{m}.\]](/images/math/d/2/7/d272d9a77f5c05c819ce3d63089929dc.png)
Most vizsgáljuk meg ugyanezen rendszer áramzaját külső feszültség nélkül. (Tételezzük fel, hogy a vizsgált vezető mintánk két végét egy árammérővel összekötve mérjük az áramfluktuációkat.) A karakterisztikus időnként elszenvedett ütközések miatt az áram korrelációja is elvész. Ezt egy időállandóval jellemzett exponenciálisan lecsengő korrelációs függvénnyel modellezzük:
![\[C(\Delta t)=C_0e^{-\frac{|\Delta t|}{\tau}}.\]](/images/math/8/c/b/8cb50ea92d26e5cfbf8154d9b6460f95.png)
Ilyen korrelációs függvény esetén a zajsűrűségre a következő érték adódik:
![\[s_I(\omega)=2c(\omega)=2\int_{-\infty}^{\infty}dte^{-i\omega t}C_0e^{-\frac{|\Delta t|}{\tau}}=\frac{4C_0\tau}{1+\omega^2\tau^2}.\]](/images/math/2/0/7/20768e384b97f92ab829ba61c33e9941.png)
A feladat tehát nem más, mint a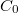 
érték, azaz az áram teljes szórásnégyzetének a meghatározása a Drude-modell segítségével.
Vizsgáljunk egy 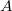keresztmetszetű, 
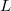hosszúságú téglalap alakú dobozt. Ebben egy elektron árama a következőképpen fejezhető ki:
![\[I_1=-Anev_x(t)=-\frac{e}{L}v_x(t),\]](/images/math/4/e/b/4ebadeb87b1e436313b4ff6c953affdf.png)
ahol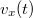 
a részecske 
irányú, azaz a doboz hosszanti irányába mutató sebessége adott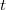 
időpillanatban.
Innen következik egy elektron áram-áram korrelációs függvénye:
![\[\langle (\Delta I_1(t))^2\rangle=\frac{e^2}{L^2}\langle v_x^2(t)^2\rangle.\]](/images/math/9/f/b/9fb04c1d2167158df99085550836afbd.png)
N független elektronra a szórásnégyzetek összeadódnak:
![\[\langle (\Delta I(t))^2\rangle=C_0=N\langle (\Delta I_1(t))^2\rangle=N\frac{e^2}{L^2}\langle v_x^2(t)\rangle.\]](/images/math/c/6/9/c69c4ba2e2224f9544750bd1347d921e.png)
Bővítsük a törtet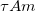 
-mel, hogy észrevegyük benne a Drude-modell vezetőképességét:
![\[C_0=\frac{N}{AL}\frac{e^2\tau}{m}\frac{A}{L}\frac{1}{\tau}m\langle v_x^2(t)\rangle =\frac{G}{\tau}m\langle v_x^2(t)\rangle.\]](/images/math/b/f/3/bf3b4bc698599d537c0d1d7b318041cc.png)
Tovább egyszerűsödik a képlet a klasszikus ekvipartíciós tételt alkalmazva:
![\[C_0=\frac{G}{\tau}k_BT.\]](/images/math/e/0/c/e0c9b547ca4a0e0d53c308478bda303b.png)
Ezt felhasználva, továbbá élve azzal a közelítéssel, hogy a frekvencia sokkal kisebb az átlagos ütözkési idő reciprokánál, adódik a termikus áramzaj spektrális sűrűsége:
![\[s_I(\omega)=\frac{4C_0\tau}{1+\omega^2\tau^2}=\frac{4k_BTG}{1+\omega^2\tau^2}\approx 4k_BTG.\]](/images/math/c/f/6/cf603a783cd205ed68579aa19284d006.png)
Felhasználva, hogy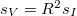 
a feszültségzaj spektrális sűrűsége:
![\[s_V=4k_BTR.\]](/images/math/9/d/5/9d568e509d842e9eba8731ca66db5a51.png)
Ezzel számítással is beláttuk a termikus zaj fehér zaj jellegét, továbbá azt is látjuk, hogy a zaj mértéke arányos a hőmérséklettel és az ellenállás nagyságával.
Meg kell jegyezni továbbá, hogy a számolás két helyen sem volt teljesen korrekt. Egyrészt csak a Fermi-energia körüli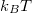 
energiasávban lévő elektronok tekinthetők valamilyen szinten függetlennek, a mélyebb energiákon lévő elektronállapotok mindegyike teljesen betöltött, így az áramfluktuációjuk zérus. Másrészt a Fermi-Dirac-eloszlást követő elektronok sebességét nem írhatjuk le az ekvipartíció tétellel, hanem a zajhoz járulékot adó részlegesen betöltött elektronállapotok alapvetően a Fermi-sebességgel mozognak.
Ez a két hiba kompenzálja egymást, és korrekt szilárdtestfizikai számításokkal is a végeredményben kapott képlettel azonos eredményre jutunk.
Poisson zaj
A Poisson-zaj az elektronok diszkrét töltéséből fakadó áramzajnak, azaz a sörétzaj egy speciális fajtája. A Poisson-zaj specialitását az egymástól független elektronok detektálása jelenti. Az elnevezése is innen származik, hiszen ahogyan a klasszikus példában a véletlen időközönként elsütött puskagolyók, úgy az egymástól függetlenül kilépő elektronok száma is Poisson-eloszlást mutat. A Poisson-eloszlás sörétzaj szempontjából fontos tulajdonsága, hogy a várható értéke megegyezik a szórásnégyzetével:
![\[\langle N\rangle=\langle (\Delta N)^2\rangle.\]](/images/math/0/c/b/0cbf76e8a53c85f26d6b4cbeaafb2b77.png)
Tegyük fel, hogy 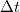idő alatt átlagosan N elektron lép ki az egyik elektródából. Ekkor az áram várható értéke a következőképpen definiálható:
![\[\langle I\rangle=\langle N\rangle\frac{e}{\Delta t}.\]](/images/math/4/3/1/43134253ea237625df6026d88d1889a6.png)
Az áram szórásnégyzete pedig felhasználva a várható érték és szórásnégyzet közötti egyenlőséget:
![\[\langle (\Delta I)^2\rangle=\langle (\Delta N)^2\rangle\left(\dfrac{e}{\Delta t}\right)^2=\langle I\rangle\frac{e}{\Delta t}.\]](/images/math/9/e/5/9e543806163d27007b6da7d9ad38faa8.png)
Ebben az esetben azonban a 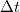nem a fentebb definiált két diszkrét mintavételezés között eltelt időt jelenti, hanem azt az időintervallumot, amelyen belül az áram várható értéke 
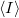, illetve szórásnégyzete 
.
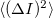Határozzuk meg ebben az időintervallumban az átlagos áramot. Ehhez a jelünket konvolváljuk össze egy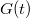 
függvénnyel, amely egyenlő 
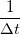-vel, ha 
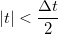, egyébként nulla.
![\[I_{out}(t)=\int_{-\infty}^{\infty}dt'I_{in}(t')G(t-t')=\frac{1}{\Delta t}\int_{t-\frac{\Delta t}{2}}^{t+\frac{\Delta t}{2}}dt'I_{in}(t').\]](/images/math/f/d/d/fdda2738e77acc0eb16abe5aa0d08a3d.png)
A konvolúció Fourier-transzformáltja a Fourier-transzformáltak szorzatával egyenlő:
![\[i_{out}(\omega)=i_{in}(\omega)g(\omega).\]](/images/math/8/2/9/829367a8b41b6331e7bc923cc438ff6e.png)
Ez az összefüggés azt sejteti, hogy a konvolváló függvény szűrőként viselkedik. Mivel a zaj az áram Fourier-transzformáltjának négyzetével arányos az áramzajok aránya a szűrő karakterisztika Fourier-transzformáltjának négyzete lesz:
![\[s_{out}(\omega)=s_{in}(\omega)g^2(\omega).\]](/images/math/7/5/9/759ca2234c0102cf091504ed2482f1c8.png)
Vizsgáljuk meg a szűrő karakterisztikáját:
![\[g(\omega)=\int_{-\infty}^{\infty}dtg(t)e^{-i\omega t}=\frac{1}{\Delta t}\int_{-\frac{\Delta t}{2}}^{+\frac{\Delta t}{2}}dte^{-i\omega t}=\frac{2}{\omega \Delta t}sin\left(\frac{\omega \Delta t}{2}\right).\]](/images/math/2/6/9/269f158eea7317a97e5628f40d665bef.png)
A továbbiakhoz bevezetjük az ekvivalens zaj sávszélesség (Equivalent Noise Bandwidth, ENBW) fogalmát. Az ENBW az a sávszélesség, amelyen fehér zajt feltételezve ugyanakkorának adódik az áram szórásnégyzete, mint a szűrőnkön mérve.
![\[\langle (\Delta I)^2\rangle=\frac{1}{2\pi}\int_{0}^{\infty}d\omega s_{out}(\omega)=\frac{s_0}{\pi \Delta t}\int_{0}^{\infty}\frac{sin^2(x)}{x^2}=\frac{s_0}{2\Delta t}=s_0f_{max}.\]](/images/math/c/a/2/ca22cb4ebe7355290d5225c1e22fd173.png)
Azaz az ekvivalens zaj sávszélesség:
![\[ENBW=\frac{1}{2\Delta t}.\]](/images/math/7/c/e/7ce1c947eb5c347f8259226055c573ec.png)
Ez az összefüggés érezhetően összecseng a Nquist-Shannon mintavételezési törvénnyel. Ha egy 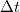időablakra átlagolunk egy jelet, az a konvolúció egy olyan szűrőként viselkedik a frekvenciatérben, melyen keresztül fehér zajt mérve az áram szórásnégyzet egyenlő lesz egy 
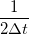tökéletes sávszűrőn mért szórásnégyzettel.
Most vizsgáljuk az áram szórásnégyzetét:
![\[\langle (\Delta I)^2\rangle=\langle I\rangle\dfrac{e}{\Delta t}=\int_{0}^{\infty}s_I(f)g(f)df=\int_{0}^{\frac{1}{2\Delta t}}s_I(f)df.\]](/images/math/c/2/0/c20ebbde3fd6c7b498184f399cf0c8ab.png)
Ez bármely 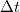szélességű átlagolási időre csak akkor teljesülhet, ha a zajsűrűség független a frekvenciától, értéke pedig:
![\[s_I(f)=2e\langle I\rangle.\]](/images/math/0/b/7/0b7c201ad4cc0af42ed36530052db89f.png)
Aliasing jelenség
A DFT a mért jel spektrumát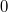 
és 
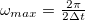frekvenciák közötti diszkrét pontokon értékeli ki. Felmerül a kérdés, hogy egy 
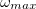-nál nagyobb frekvenciakomponenseket tartalmazó jelnél mi történik a magas frekvenciakomponensekkel.
Vizsgáljunk egy 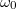frekvenciájú tiszta szinuszos jelet:
![\[F(t)=A_0e^{i\omega_0t}.\]](/images/math/2/4/5/245b0442ddc0df9d07406191c01c8389.png)
Vegyük ennek a jelnek a Fourier-transzformáltját:
![\[f(\omega)=\int_{-\infty}^{\infty}A_0e^{i\omega_0t}e^{-i\omega t}dt=A_02\pi\delta(\omega-\omega_0).\]](/images/math/8/8/7/88791b26a657f44c0a4a149987bb78bc.png)
A jel Fourier-transzformáltja tehát a várakozásnak megfelelően egy Dirac-delta. Most nézzük meg, hogy a DFT számolása során hogyan változik a spektrum meghatározása a gyakorlatban.
![\[DFT(\omega_k)=\sum_{n=0}^{N-1}A_0e^{i\omega_0n\Delta t}W(n\Delta t)e^{-i\omega_k n\Delta t}\Delta t.\]](/images/math/7/7/4/77454b64a192deb67b7e8ea793f4485d.png)
Vegyük észre, hogy
![\[DFT(\omega_k)=DFT\left(\omega_k+\frac{2\pi m}{\Delta t}\right),\]](/images/math/f/d/3/fd376985dc4b0bb692451f12d2b4dc6c.png)
ahol 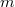egész szám. Másrészt
![\[DFT(\omega_k)=DFT^*(-\omega_k),\]](/images/math/5/e/6/5e6d6b14e0209e2955a599f2e5c37a67.png)
azaz
![\[\left|DFT(\omega_k)\right|=|DFT(-\omega_k)|.\]](/images/math/8/0/d/80ddbb4ed0ee9ca1958dfae37b6c7c3e.png)
Így belátható, hogy tetszőleges magas körfrekvenciájú jelet úgy látunk, mint ha az a ![\setbox0\hbox{$\left[0,\omega_{max}=\dfrac{2\pi}{2\Delta t}\right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/1/d/5/1d5edc142dda0da53e19be6704cd946e.png)
tartományban lévő jel lenne a saját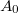 
amplitúdójával.
A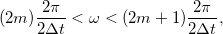 
frekvenciatartományokban lévő komponensek az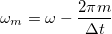 
frekvencián jelennek meg a spektrumban, míg a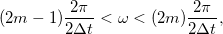 
tartományokban lévők a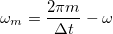 
frekvencián.
A fentiekkel beláttuk, hogy minden 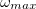-nál nagyobb frekvenciatag megjelenik a DFT-t követően a diszkrét frekvenciákat tartalmazó ![\setbox0\hbox{$[0,\omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/5/8/9/589da9a19c34b829d19740c9873851cf.png)
tartományban. Gondoljuk át, hogy a végeredményben kapott DFT spektrum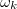 
pontjában összeadódnak-e a 
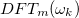tagok amplitúdói 
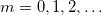értékekre. Mivel ezen frekvenciatagok fázisai nem azonosak, így a különböző 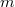értékekhez tartozó amplitúdók nem adhatóak össze.
Később látni fogjuk, hogy a zajsűrűség számításához a DFT abszolútérték négyzetére van szükség, amely azonban a véletlenszerű, egymástól független fázisok miatt egyenlő a különböző 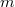értékekre vett amplitúdók négyzeteivel:
![\[|DFT(\omega_k)|^2=\left(\sum_{m}^{} DFT_m(\omega_k)\right)\left(\sum_{m}^{} DFT^*_m(\omega_k)\right)=\sum_{m}^{}|DFT_m(\omega_k)|^2.\]](/images/math/1/7/b/17bbdbf920eb8fad23dd47b01b2d3d7f.png)
A leképezés leginkább úgy képzelhető el, mint a magas frekvenciás tartományok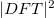 
-einek a intervallumra történő visszahajtogatása. Az 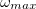fölötti részt visszahajtjuk ![\setbox0\hbox{$[-\infty; \omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/7/e/1/7e1583c668f4dc9fea3cf73d3c7fb0ab.png)
intervallumra. Majd ezt a visszahajtott spektrumot 0 
-nél előrehajtjuk, stb. Ezt mindaddig folytatjuk, amíg minden jelentős frekvenciakomponenst be nem hajtottunk a intervallumba.
Beláttuk, hogy a magas komponensű jelek fals spektrumot okozhatnak, így gondoskodni kell kiszűrésükről egy aluláteresztő szűrővel. Ezt a jelenséget aliasingnak, azaz magas frekvenciájú komponensek beszűrődésének nevezzük. Fontos megjegyezni, hogy az aliasing kialakulásának az oka a DFT diszkrét mintavételezése, és független a mérési pontok 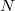számától. A gyakorlatban a legtöbbször az erősítők, vagy a mérőkártyák rendelkeznek anti-aliasing szűrővel, ami a maximális frekvencia fölött rendszerint élesen levágja a spektrumot.
