A szilárdtestfizika alapjai

Általános adatok

• Kód: BMETE11AF05;
• Követelmény: 2/0/0/V/2;
• Félév: ősz;
• Nyelv: magyar;
• Előadó: Dr. Mihály György egyetemi tanár
• Jelenléti követelmények: A félév végi aláírás feltétele előadások legalább 70%-án való részvétel. Az előadásokon jelenléti ívet vezetünk.
• Félévközi számonkérések: azonosak a Szilárdtestfizika gyakorlat számonkéréseivel.
• Félév végi osztályzat: írásbeli és szóbeli vizsga. A vizsga feltétele az aláírás, valamint a gyakorlati jegy megszerzése.

Időbeosztás (2015 ősz)

Az első előadása szeptember 10-én (csütörtök) 14-16 óra között lesz az F 213 teremben (ez a gyakorlatok időpontja, a gyakorlatok egy héttel később indulnak).

• Előadások: kedd 14-16, F. épület III. lépcsőház 2.emelet 13.
• Konzultációk: hétfő 14-18 (előzetes bejelentkezés alapján a mihaly.gyorgy@mail.bme.hu email címen);

Az előadások rövid kivonata - jegyzetelésre alkalmas formában - letölthető az előadás címére kattintva. A kivonatok önmagukban nem alkalmasak a tananyag elsajátítására, de megkönnyítik a jegyzetelést (tartalmazzák az összes lényeges formulát), így elősegítik az előadásra való koncentrálást.

szept. 8. Szilárd testek

szept. 15. Szerkezetmeghatározás, szóráskísérletek

szept. 22. Kristályok szimmetriái

szept. 29. Szimmetriák szerepe a szilárdtestfizikában (habilitációs előadás)

okt. 6. Rácsrezgések

okt. 13. Szilárd testek fajhője

okt. 20. Fémek kvantummechanikai leírása

okt. 27. Közel szabad elektron modell

nov. 3. szoros kötésű közelítés

nov. 10. Fémek, félvezetők

nov. 24. Fermi-felület

dec. 1. Fermi-felület kísérleti meghatározása

dec. 8. Összefoglalás

Részletes tematika

Kristálytan - Szerkezetvizsgálat

Kristály: elemi cella, Wigner-Seitz cella; kristály síkok, Miller-index; reciprok rács, Brillouin-zóna

Kristályrendszerek (eltolás + egy definiáló szimmetria); Bravais-rácsok (élhossz és szögek szerinti osztályozás); pontcsoportok és tércsoportok

Diffrakció elmélete: Bragg-feltétel; Laue féle leírás; szerkezeti tényező és atomi alaktényző

Rugalmas szóráskisérletek: Ewald szerkesztés, Debye-Scherrer- és Laue-módszer; Röntgen-, elektron- és neutron-szórási mechanizmus; szinkrotron-sugárzás; kvázikristályok

Rácsrezgések - fononok

Klasszikus leírás: lineáris lánc rezgései; rácsrezgések 3 dimenzióban (Dinamikus mátrix sajátérték-egyenlete); diszperziós reláció; állapotsűrűség

Kvantummechanikai leírás: Fonon-energia és impulzus; Bose-Einstein statisztika; a fonongáz fajhője

A diszperziós reláció kisérleti meghatározása: megmaradási tételek részecske-fonon, ill. foton-fonon kölcsönhatáskor; rugalmatlan neutron-szórás

Elektronok

Szabad elektrongáz kvantummechanikai leírása: Fermi-Dirac statisztika; Sommerfeld-sorfejtés; fajhő, mágneses szuszceptibilitás

Elektronok periodikus potenciálban: Bloch-tétel; diszperziós reláció perturbációs számolása; szoros-kötésű közelítés

Sávszerkezet: kváziklasszikus közelítés, effektív tömeg; Fermi-felület kísérleti meghatározása; fémek-félvezetők-szigetelők

Drude-modell: vezetőképesség, Hall-állandó, fémek optikai tulajdonságai

Tételek

• Kristályrács definíciója. Reciprok-rács, kristálysíkok, Miller-index. Szimmetriaműveletek, kristályrendszerek, Bravais-rácsok.
• Diffrakció elmélete. Szerkezeti tényező, atomi szórási tényező. Röntgen-, elektron- és neutron-szórási kísérletek.
• Rácsrezgések diszperziós relációja. A dinamikus mátrix sajátérték-egyenlete. Akusztikus és optikai ágak. A diszperziós reláció kísérleti meghatározása.
• Szilárd testek fajhőjének kvantummechanikai leírása. Bose-Einstein eloszlás. Az állapotsűrűség számolása. Debye-modell.
• Szabad elektrongáz kvantummechanikai leírása. Fermi-Dirac eloszlás. Elektron-fajhő, fémek mágneses szuszceptibilitása (Sommerfeld-sorfejtés).
• Bloch-tétel. Közel szabad elektron modell. Sávszerkezet. Fermi-felület kísérleti meghatározása.
• Wannier-függvények. Szoros kötésű közelítés. Lokalizált és kiterjedt elektronállapotok.
• Hullámcsomag. Effektív tömeg, fémek-félvezetők. Drude-modell: Hall-állandó, $\sigma$($\omega$), $\epsilon$($\omega$).

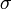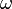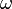Irodalom

Sólyom Jenő: A modern szilárdtestfizika alapjai I-II (második kiadás), Eötvös Kiadó, Budapest (2009).
Ajánlott olvasmány: Kivonatok "bevezető" kvantummechanika jegyzetből,