Experiments with Polarized Light
--Investigation of Liquid Crystal Displays--
---Liquid Crystals---
Liquid crystal (LC) is a state of matter that is intermediate between the crystalline
solid and the amorphous liquid. The nematic LCs are organic compounds consisting of
long-shaped needle-like molecules. The orientation of the molecules can be easily aligned
and controlled by applying an electrical field. Uniform or well prescribed orientation of the
LC molecules is required in most LC devices. The structure of the LC cell used in this
experiment is shown in Fig 1. Rubbing the polyimide film can produce a well-aligned
preferred orientation for LC molecules on substrate surfaces, thus due to the molecular
interaction the whole slab of LC can achieve uniform molecular orientation. The local
molecular orientation is called the director of LC at that point.
The LC cell exhibits the so-called double refraction phenomenon with two principal
refractive indices. When light propagates along the direction of the director, all polarization
components travel with the same speed 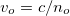 , where
, where 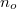 is called the ordinary index of
refraction. This propagation direction (direction of the director) is called the optical axis of
the LC cell. When a light beam propagates in the direction perpendicular to the optical axis,
in general, there are two speeds of propagation. The electric field of the light polarized
perpendicular (or parallel) to the optical axis travels with the speed of
is called the ordinary index of
refraction. This propagation direction (direction of the director) is called the optical axis of
the LC cell. When a light beam propagates in the direction perpendicular to the optical axis,
in general, there are two speeds of propagation. The electric field of the light polarized
perpendicular (or parallel) to the optical axis travels with the speed of 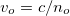 (or
(or
 , where
, where 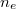 is called the extraordinary index of refraction). The birefringence
(optical anisotropy) is defined as the difference between the extraordinary and the ordinary
is called the extraordinary index of refraction). The birefringence
(optical anisotropy) is defined as the difference between the extraordinary and the ordinary
\setbox0\hbox{$\Delta n = n_e − n_o$}%
\message{//depth:\the\dp0//}%
\box0%
.