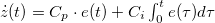Investigation of atomic contacts
The purpose of the measurement is to investigate the transport properties of atomic-sized contacts using the MyDAQ data acquisition card. For this purpose, the conductance curves of nanojunctions are recorded in the last moments before rupture, when only a few atoms connect the two sides. The acquired conductance traces are statistically examined using a conductance histogram.
Introduction: atomic sized contacts
Nowadays, an increasingly important and rapidly growing field of physics research is the study of various nanostructures with a typical width of several hundred - or as we will see - single atoms. Devices of nanometer scale exhibit many astonishing quantum physics processes, as the size of the system becomes comparable to the mean free path of electrons or even to the wavelength of the electrons, and in the case of very small, atomic systems, the atomic quantization of matter must be also taken into account. In addition to studying quantum physical phenomena as part of basic research, nanostructures are playing an increasingly important role in the miniaturization and development of electronic devices. The fabrication of most nanostructures requires a strong technical background based on electron beam lithography, and many quantum physics processes can only be studied at extremely low temperatures (4 K-10 mK). In this measurement we study a nanophysical phenomenon that can be observed at room temperature with a relatively simple measurment system, although the structure under investigation is probably one of the smallest nanostructures: a contact in which two electrodes are connected by a single atom.
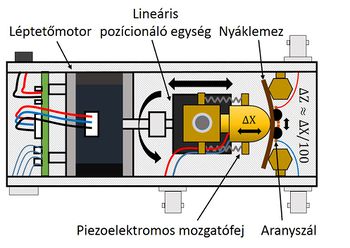
A single atom contact is surprisingly easy to create, since at the last moment of breaking a metal wire a single atom connects the two sides. However, the stabilization of the contact is a major challenge, since it is a prerequisite that the mechanical stability of the measuring device is significantly better than a typical atom to atom distance (~ 300 pm). Such conditions can be achieved with a high-stability low-temperature tunnel microscope or with the so-called MCBJ technique (Mechanically Controllable Break Junction technique). The principle of this method is illustrated in Figure 1. The contact is made of a simple metallic wire which is fixed with two adhesive dots on a bending beam. By bending the beam, the attachment points are moving apart so that the metallic wire can be broken. It follows from the mechanical arrangement of the instrument that, when the bending beam is bent in the centre by a gently movable axis, the relative displacement of the electrodes is only 1/100 of the displacement of the axis. If measurements are made at extremely low temperatures in a liquid helium environment and a finely tuneable piezo actuator is used to bend the beam, mechanical stability of up to a few pm can be achieved, which is by an order of magnitude better than what can be achieved using a scanning tunnel microscope.
| 1. ábra. The sketch of the MCBJ setup. |
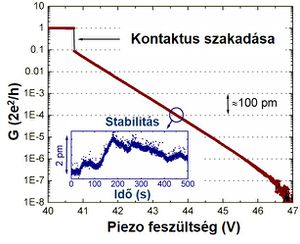
The stability of the system can be tested using the effect of quantum mechanical. If the electrodes are gently moved closer after breaking of the metallic wire, before direct contact occurs, a tunnel current flows between the two sides, the magnitude of which is an exponential function of the electrode spacing. It is calculated that the tunnel current increases approximately tenfold when the electrodes are approached by 100 pm. In low temperature experiments, the exponential distance dependence can be detected through about six orders of magnitude (Figure 2), that is, the conductance increases by about one million times while the electrodes are only approached by 600 µm (two to three times the typical atomic distance). This phenomenon allows for very sensitive detection of changes in the distance between the electrodes. The inset of Figure 2 shows that at a fixed piezo voltage, the electrode spacing changes by only 2 µm in ten minutes, which is about one hundredth of a typical atomic atom spacing. The figure also shows that as the electrodes are approached, a sudden jump is observed at a given point, followed by a conductivity plateau. This creates a direct metallic contact, which in most cases consists of a single atom.
| 2. ábra. Alagútáram és stabilitás mérése alacsony hőmérsékleti MCBJ mérőrendszerben. |
Az ábrán látható, hogy az elektródák közelítése közben egy adott ponton egy hirtelen ugrást tapasztalunk, melyet egy vezetőképesség plató követ. Ekkor egy közvetlen, fémes kontaktus jön létre, mely a legtöbb esetben egyetlen atomból áll.
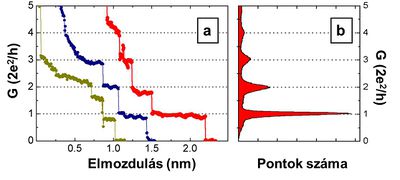
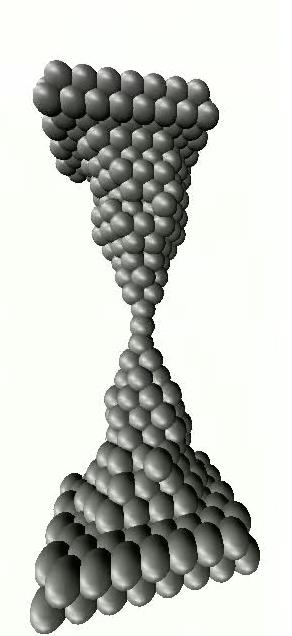
Most közelítsük meg az egyatomos kontaktus kialakulását a másik oldalról, és vizsgáljuk meg a vezetőképesség változását a fémszál szétszakítása közben. Ahogy a szál vékonyodik, először folytonosan csökkenő vezetőképességet tapasztalunk. Ha viszont a kontaktus átmérője már eléri a pár atomot, a vezetőképesség már nem tud folytonosan változni az atomi kvantáltság miatt. A 3/a. ábra bal oldali panelje nanokontaktusok szétszakítása közben felvett vezetőképesség-görbéket mutat. A kontaktus két oldalának széthúzása közben először az atomok csak rugalmasan mozdulnak el egymáshoz képest, miközben a vezetőképesség csak mérsékelten változik (platók). Egy bizonyos feszítés után viszont az atomok ugrásszerűen átrendeződnek, és egy kevesebb atomot tartalmazó, kedvezőbb konfiguráció jön létre. Az atomi átrendeződéseket a vezetőképesség ugrásszerű változása tükrözi. Mikor a teljes szétszakadás előtti utolsó platót látjuk, a két oldalt már csak egyetlen atom köti össze. Ha a szakítás után a két elektródát összenyomjuk, a szakítási felületen az atomok újra összekapcsolódnak, így a nanovezeték szakítását újra és újra megismételhetjük (3/c. ábra). Természetszerűleg, minden egyes nanokontaktus szétszakításakor a vezetőképesség-görbék máshogyan néznek ki, bár jellegre hasonlóak (lásd a 3/a. ábra különböző vezetőképesség-görbéit). Egy adott anyagból készült nanokontaktusok karakterisztikus jellemzőit statisztikai módszerrel térképezhetjük fel. Nagyszámú szétszakítás közben felvett vezetőképesség görbéből felrajzolhatunk egy hisztogramot, mely megmutatja hogy a szétszakítások közben egy adott vezetőképesség-értéket milyen gyakorisággal láthattunk (3/b. ábra). A hisztogramban kirajzolódó csúcsok megmutatják a stabil, nagy gyakorisággal létrejövő atomi konfigurációk vezetőképességét. A hisztogram első csúcsa az egyatomos kontaktus vezetőképességét adja meg. Érdemes megemlíteni, hogy bizonyos anyagokban, pl. aranyban egy egyatomos kontaktus a további széthúzás hatására még nem szakad szét, hanem akár hét atom hosszúságú, egyetlen atom átmérőjű atomlánc is képződhet, ahogy ez a 3/c. ábrán látható szimuláció is szemlélteti.
| 3/a-b. ábra. Atomi méretű arany nanovezetékek szakítás közben felvett vezetőképesség-görbéi (bal oldal). Az egymás utáni szakítások jellegre hasonló, de a részletekben különböző vezetőképsség-görbéket adnak. Sok szakítás vezetőképesség-görbéi alapján felrajzolhatunk egy vezetőképesség-hisztogramot (jobb oldal), melyben a csúcsok a gyakran kialakuló atomi konfigurációk vezetőképességeit adják meg. | 3/c. ábra. Fém nanovezeték ismételt szakítása (számítógépes szimuláció). |
Az egyatomos kontaktus vezetési mechanizmusának megértéséhez kvantummechanikai megközelítésre van szükség, hiszen a kontaktus átmérője azonos méretskálájú az elektronok hullámhosszával. A vezetés kvantált vezetési csatornákon keresztül történik, melyek vezetőképessége nem haladhatja meg a kvantumvezetőképesség-egységet, 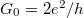 .
.
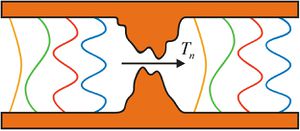
4. ábra Egy nanokontaktus vezetési tulajdonságait modellezhetjük két ideális (párhuzamos falú) kvantumvezeték közötti szórási tartománnyal, melyen a bal oldali n-edik vezetési csatornából a jobb oldali n-edik vezetési csatornába 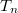 valószínűséggel transzmittálódnak az elektronok. valószínűséggel transzmittálódnak az elektronok.
|
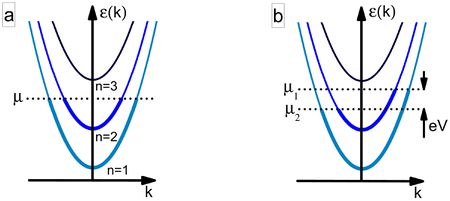
| 5. ábra (a) Diszperzós reláció ideális kvantumvezetékben. (b) Diszperzós reláció a mintára feszültséget kapcsolva. |
A vezetőképesség-kvantum megértéséhez vizsgáljunk meg egy ideális kvantumvezetéket. (Mindezekről részletesebb leírás található a nanofizika tudásbázisban!) Képzeljünk el egy két elektródát összekötő ballisztikus vezetéket, melyben nincsenek szórócentrumok, mint például a 4. ábra bal vagy jobb oldali, párhuzamos falú tartománya. Az elektronok mozgását a vezetékben a Schrödinger-egyenlet írja le, keresztirányban kvantált módusok alakulnak ki, hosszirányban pedig egydimenziós síkhullámként propagálnak az elektronhullámok. A diszperziós reláció 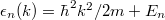 alakú, ahol
alakú, ahol 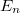 a keresztirányú módus energiája. Az egyes keresztmódusokhoz tartozó diszperziókat vezetési csatornának nevezzük. Nyitott csatornáról beszélünk, ha a diszperziós reláció metszi a kémiai potenciált,
a keresztirányú módus energiája. Az egyes keresztmódusokhoz tartozó diszperziókat vezetési csatornának nevezzük. Nyitott csatornáról beszélünk, ha a diszperziós reláció metszi a kémiai potenciált, 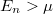 esetén viszont zárt a csatorna, azaz nem propagálnak benne elektronok. Számoljuk ki a kvantumvezeték vezetőképességét egyetlen vezetési csatorna esetén. Az elektródákra feszültséget kapcsolva a kémiai potenciálok eltolódnak
esetén viszont zárt a csatorna, azaz nem propagálnak benne elektronok. Számoljuk ki a kvantumvezeték vezetőképességét egyetlen vezetési csatorna esetén. Az elektródákra feszültséget kapcsolva a kémiai potenciálok eltolódnak 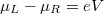 -vel, így a balról jobbra propagáló állapotok
-vel, így a balról jobbra propagáló állapotok 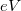 -vel magasabb energiáig vannak betöltve, mint a jobbról balra menő állapotok. A betöltések eltolódása miatt a pozitív és negatív irányú áram nem egyenlő, így a vezetékben
-vel magasabb energiáig vannak betöltve, mint a jobbról balra menő állapotok. A betöltések eltolódása miatt a pozitív és negatív irányú áram nem egyenlő, így a vezetékben 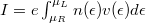 nettó áram folyik, ahol
nettó áram folyik, ahol 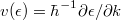 az elektronok sebessége,
az elektronok sebessége, 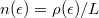 pedig az elektronsűrűség, ahol
pedig az elektronsűrűség, ahol  a vezeték hossza,
a vezeték hossza, 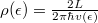 pedig az egydimenziós állapotsűrűség. Behelyettesítés után
pedig az egydimenziós állapotsűrűség. Behelyettesítés után 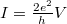 adódik, azaz az egy vezetési csatornának megfelelő vezetőképesség-kvantum
adódik, azaz az egy vezetési csatornának megfelelő vezetőképesség-kvantum 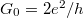 , amely 12906 Ω ellenállásnak felel meg. Az eredményt általánosíthatjuk, ha több vezetési csatornát is figyelembe veszünk, és minden csatornában megengedünk egy véges transzmissziós valószínűséget (4. ábra). A rendszert kezelhetjük egy megfelelő saját bázisban, melyben a bal oldali n-edik vezetési csatornából csak a jobb oldali n-edik vezetési csatornába szóródhatnak elektronok. Ez alapján egy tetszőleges nanokontaktus vezetőképességét az ún. Landauer-formula segítségével adhatjuk meg:
, amely 12906 Ω ellenállásnak felel meg. Az eredményt általánosíthatjuk, ha több vezetési csatornát is figyelembe veszünk, és minden csatornában megengedünk egy véges transzmissziós valószínűséget (4. ábra). A rendszert kezelhetjük egy megfelelő saját bázisban, melyben a bal oldali n-edik vezetési csatornából csak a jobb oldali n-edik vezetési csatornába szóródhatnak elektronok. Ez alapján egy tetszőleges nanokontaktus vezetőképességét az ún. Landauer-formula segítségével adhatjuk meg:
![\[G=\frac{2e^2}{h}\sum\limits_{n}{} T_n,\]](/images/math/d/5/6/d56db0d04c0942a7a2fc310e2d833b09.png)
ahol 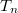 az
az  -edik csatorna transzmissziós valószínűsége. Egy adott nanokontaktus jól jellemezhető a vezetési csatornák számával, és az egyes csatornák transzmissziós valószínűségeivel, így a transzmissziós együtthatók halmazát gyakran a nanokontaktus mezoszkópikus PIN-kódjának hívják.
-edik csatorna transzmissziós valószínűsége. Egy adott nanokontaktus jól jellemezhető a vezetési csatornák számával, és az egyes csatornák transzmissziós valószínűségeivel, így a transzmissziós együtthatók halmazát gyakran a nanokontaktus mezoszkópikus PIN-kódjának hívják.
A 3. ábrán bemutatott vezetőképesség-görbéken ill. hisztogramon látjuk, hogy arany kontaktus szétszakításakor az egyatomos kontaktusnak megfelelő utolsó plató a 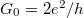 vezetőképesség-kvantumhoz közel helyezkedik el. Ebből szigorúan véve még nem következik, hogy egyetlen, tökéletesen transzmittáló csatorna adja-e a vezetést, hiszen véletlen egybeesésként több részlegesen részlegesen áteresztő vezetési csatorna együttes vezetőképessége is kiadhat
vezetőképesség-kvantumhoz közel helyezkedik el. Ebből szigorúan véve még nem következik, hogy egyetlen, tökéletesen transzmittáló csatorna adja-e a vezetést, hiszen véletlen egybeesésként több részlegesen részlegesen áteresztő vezetési csatorna együttes vezetőképessége is kiadhat 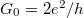 -nak megfelelő vezetőképességet. Ennek megállapításához további mérések szükségesek, melyek nem csak a transzmissziós együtthatók összegét mérik, hanem további információt nyújtanak a transzmissziós együtthatókról. Példaként említhetjük a sörétzaj mérését. Ha a vezetőképesség átlagértéke mellett a vezetőképesség időbeli fluktuációit is mérjük, a
-nak megfelelő vezetőképességet. Ennek megállapításához további mérések szükségesek, melyek nem csak a transzmissziós együtthatók összegét mérik, hanem további információt nyújtanak a transzmissziós együtthatókról. Példaként említhetjük a sörétzaj mérését. Ha a vezetőképesség átlagértéke mellett a vezetőképesség időbeli fluktuációit is mérjük, a 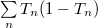 mennyiség is meghatározható. Látszik, hogy egyetlen tökéletesen transzmittáló csatorna esetén a sörétzaj eltűnik, míg több, részlegesen transzmittáló csatorna esetén véges zajt kapunk. Az arany kontaktuson végzett zajmérések egyértelműen megmutatták, hogy az egyatomos arany kontaktus
mennyiség is meghatározható. Látszik, hogy egyetlen tökéletesen transzmittáló csatorna esetén a sörétzaj eltűnik, míg több, részlegesen transzmittáló csatorna esetén véges zajt kapunk. Az arany kontaktuson végzett zajmérések egyértelműen megmutatták, hogy az egyatomos arany kontaktus 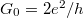 vezetőképességét 1 db tökéletesen áteresztő csatorna adja. Elméleti megfontolások alapján ez azzal hozható összefüggésbe, hogy aranyban csak az s elektronok vesznek részt a vezetésben. Például d-fémekben, ahol az egyatomos kontaktus vezetéséhez a d elektronok is hozzájárulnak akár 5 részleges transzmissziójú nyitott csatornát is megfigyelhetünk. Megjegyezzünk, hogy a jelenség különbözik a két dimenziós heterostruktúrákban megfigyelhető vezetőképesség kvantálástól vagy a kvantum Hall effektustól , ahol csak teljesen nyitott és zárt csatornák vannak jelen.
vezetőképességét 1 db tökéletesen áteresztő csatorna adja. Elméleti megfontolások alapján ez azzal hozható összefüggésbe, hogy aranyban csak az s elektronok vesznek részt a vezetésben. Például d-fémekben, ahol az egyatomos kontaktus vezetéséhez a d elektronok is hozzájárulnak akár 5 részleges transzmissziójú nyitott csatornát is megfigyelhetünk. Megjegyezzünk, hogy a jelenség különbözik a két dimenziós heterostruktúrákban megfigyelhető vezetőképesség kvantálástól vagy a kvantum Hall effektustól , ahol csak teljesen nyitott és zárt csatornák vannak jelen.
Mérési elrendezés
A laboratóriumi gyakorlaton egyatomos kontaktusok vezetését vizsgáljuk egy vékony fémszál ismételt elszakításával és összeérintésével. Mivel az egyatomos arany kontaktusok vezetőképessége közel van a vezetőképesség-kvantumhoz, illetve az összes fém közül az arany oxidálódik a legkevésbé, ezért méréseinket arany mintán végezzük. A kontaktus kontrollált mozgatása érdekében az MCBJ technikát használjuk. A laprugókra 100 μm átmérőjű nagytisztaságú aranyszálat rögzítettünk.
| 8. ábra. Nyáklapból készült rugalmas lapkára forrasztott fémszál |
A laprugó egy léptetőmotorral vezérelt lineáris mozgató, valamint egy piezoelektromos mozgató segítségével hajlítható. A mintára az MyDAQ kártya segítségével 100mV nagyságrendű feszültséget adunk, a kontaktuson folyó áramot egy 105 erősítésű áramerősítővel mérjük.
Az 1.ábrának megfelelően egy alumínium konzolba rögzítve található a léptetőmotor, a piezomozgató és a rugalmas lapkára rögzített fémszál. A motorhoz egy tápegység tartozik. A motor és a piezomozgató vezérlését, illetve a vezetőképesség mérését teljes egészében egy számítógéphez csatlakoztatott MyDAQ kártyával végezzük. A méréshez szükséges kiegészítő áramkörök egy előre összeállított próbanyákon találhatóak.
A TRINAMIC - PD3-013-42 léptetőmotor az alumínium konzolra rögzített négypólusú mikrofoncsatlakozón keresztül vezérelhető. A négy pólusból háromra digitális jeleket küldünk a mérőkártyáról. Az egyik pólussal a motor ki és bekapcsolható (ENABLED), a másik pólussal a motor forgásiránya állítható (DIRECTION), a harmadik pólusra pedig egy rövid pulzust küldve a motor egy lépést tesz, azaz körülbelül 0.1 fokkal fordul el. A negyedik pólusra a digitális jelek földje (DGND) kerül. Az áramkörhöz csatlakoztatott kábel segítségével kötjük a motort a mérőkártyához. A kábel színkiosztása: ENABLED - Kék, DIRECTION - Zöld, STEP - Narancs, DGND - Barna. Az ENABLED, DIRECTION, STEP, DGND jeleket az összeállított áramkör csatlakozója a kártya DIO0, DIO1, DIO2 és DGND kimeneteivel köti össze.
A finom mozgatáshoz Piezomechanik PSt150/3.5x3.5/20 típusú piezomozgatót használunk, mely -30 - +150 V tartományban működtethető, a teljes feszültségtartomány 28 μm elmozdulásnak felel meg. A piezot nem vezérelhetjük közvetlenül a mérőkártyáról, hiszen az nem tudna elég nagy áramot kiadni, így egy erősítőt kell közbeiktatnunk. Ez az erősítő áramkör szintén az összeállított panelen helyezkedik el. A panel egy szabványos csatlakozóval köthető az adatgyűjtő kártyához.
A méréshez rendelkezésre áll egy mérőprogram, amiben a léptető motor vezérlését implementáltuk. Itt gombnyomássokkal lehet ki vagy befele tekerni a motort, illetve a lépések számát meghatározó pulzusok számát is meg lehet adni. A mérőprogramban implementálva van továbbá az adatok beolvasásása, illetve az egyik csatornán a jelek kiadása. Ez a piezovezerléshez tartozó csatorna, és a programban példaként egy szinusz jel alapú vezérlést implementáltunk.
Mérési feladatok
1. Ismerjük meg és próbáljuk ki a kétpaneles MCBJ mérőprogramot, annak funkcióit, működését!
2. Módosítsuk a mérőprogramot úgy, hogy a kártya állítható amplitúdójú és frekvenciájú háromszögjelet adjon ki!
3. Írjunk egy rutint, mely az egymás után beolvasott görbék alapján hisztogramot készít, azaz kiszámolja a különböző feszültségértékek előfordulási gyakoriságát. Érdemes még a mérés előtt, felkészüléskor átgondolni, hogyan lehet hisztogram-készítő algoritmust megvalósítani. Mentsük ezt a hisztogrammot a mérés végén/közben egy külön fálba/változóba, hogy a jegyzőkönyv írásnál ez az adat rendelkezésre álljon.
4. Ábrázoljuk a paneleken a beolvasott vezetőképességet, valamint a kumulált hisztogramot!
5. Állítsuk össze a mérési elrendezést atomi méretű kontaktusok vizsgálatához és teszteljük a kapcsolást egy 12900 Ω-os ellenállással! Ezen az ellenálláson teszteljük a hisztogramkészítő rutint. A rutint tesztelhetjük akár a kiadott háromszög jelen is (a hozzátartozó tömbön).
6. A mintaellenállás helyére kössük a laprugóra rögzített aranyszálat! Szakítsuk el a kontaktust, és vegyünk fel egyedi vezetőképesség görbéket! Tároljunk el pár görbét, melyek szépen mutatják a vezetőképesség platókat! A léptetőmotor és a piezoelektromos mozgató együttes vezérlésével a kontaktust újra meg újra elszakítva vegyünk fel legalább 100 görbét, és készítsünk vezetőképesség hisztogramot! Ezeket a görbéket mentsük el, hogy az otthoni adatelemzés lehetséges legyen!
6. Vizsgáljuk az elszakított kontaktus összenyomását! Készítsünk olyan mérőfunkciót, amely rögzíti és ábrázolja a kontaktusok között folyó alagútáramot! Ábrázoljuk az alagútáramot logaritmikus skálán és vessük össze az irodalmi adattal!
Szorgalmi feladat: Az alagútáramot felhasználva szabályozzuk időben a két kontaktus távolságát! Ehhez a közismert PI szabályozástechnikát alkalmazzuk. A finom mozgatást kizárólag a piezó segítségével valósítsuk meg. Teszteljük a stabilitást különböző külső hatásokkal (taps, hőforrás). Segítség:
Segítség
Egy kiindulási program áll rendelkezésre a laborgyakorlathoz itt.
Az NI kártyával hajtható végre a mérőfeszültség kiadása is. Az ehhez szükséges függvény AnalogOutput, melybe egész számú mV-ban kell megadni azt a feszültséget, melyet a kártya AO0-ás kimenetén kiadni kívánunk.
void AnalogOutput(double Millivolts) { NationalInstruments.DAQmx.Task OutAnalogTask; OutAnalogTask = new NationalInstruments.DAQmx.Task(); AnalogSingleChannelWriter Analog_DAQwriter; double Minimumvoltage = -5; //DAQmx output value min double Maximumvoltage = 5; //DAQmx output value max //Analoge output on AO0 try { Analog_DAQwriter = new AnalogSingleChannelWriter(OutAnalogTask.Stream); OutAnalogTask.AOChannels.CreateVoltageChannel("myDAQ1/ao0", "", Minimumvoltage, Maximumvoltage, AOVoltageUnits.Volts); Analog_DAQwriter.WriteSingleSample(true, Millivolts / 1000); } catch (DaqException exception) { MessageBox.Show(exception.Message); } OutAnalogTask.Dispose(); }
Az NI adatgyűjtő kártya továbbá felhasználható feszültség mérésére is. Erre a kontaktus monitorozásakor van szükségünk. Az AnalogInput függvény a kártya AI1 bemenetére kötött feszültség értéket adja vissza mV-ban, double-ként.
double AnalogInput() { NationalInstruments.DAQmx.Task InputTask; InputTask = new NationalInstruments.DAQmx.Task(); AnalogSingleChannelReader Analog_DAQreader; double Minimumvoltage = 0; //DAQmx output value min double Maximumvoltage = 5; //DAQmx output value max //Analog input channel AI0 InputTask.AIChannels.CreateVoltageChannel("myDAQ1/ai1","",AITerminalConfiguration.Differential, Minimumvoltage, Maximumvoltage,AIVoltageUnits.Volts); Analog_DAQreader = new AnalogSingleChannelReader(InputTask.Stream); return Analog_DAQreader.ReadSingleSample()*1000; }
Egyéb
A korábbi mérésleírás itt található pdf formátumban.