„Az elektron töltése és a Boltzmann-állandó hányadosának (e/k) mérése. A Planck és a Boltzmann-állandó hányadosának (h/k) mérése.” változatai közötti eltérés

A Fizipedia wikiből
a
 
(2 szerkesztő 24 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 
<wlatex>
 
<wlatex>
  
−
Szerkesztés alatt!
 
  
 +
__TOC__
 +
 +
=Az elektron töltése és a Boltzmann-állandó hányadosának (e/k) mérése=
 
''A mérés célja:''
 
''A mérés célja:''
 
*termikusan aktivált folyamat tanulmányozása félvezető p–n átmenetben,
 
*termikusan aktivált folyamat tanulmányozása félvezető p–n átmenetben,
10. sor: 12. sor:
 
*összefoglaljuk a p–n átmeneten folyó áramra vonatkozó elméleti alapismereteket,(a jelenségek igen részletes leírása a megadott irodalomban olvasható),
 
*összefoglaljuk a p–n átmeneten folyó áramra vonatkozó elméleti alapismereteket,(a jelenségek igen részletes leírása a megadott irodalomban olvasható),
 
*kimérjük egy tranzisztor kollektor-áramának a bázis–emitter feszültségtől való függését, és meghatározzuk az  arányt.
 
*kimérjük egy tranzisztor kollektor-áramának a bázis–emitter feszültségtől való függését, és meghatározzuk az  arányt.
−
 
−
__TOC__
 
  
 
==Elméleti összefoglaló==
 
==Elméleti összefoglaló==
  
−
Az elektron töltése ($e$) és a Boltzmann-állandó ($k$) fontos természeti állandók, amelyek ismeretére számos jelenség leírásánál szükségünk van. Az olyan folyamatokat, amelyeknek során pl. egy részecske a továbbhaladásához szükséges energiát a termikus mozgásból származó véletlen energiaközlés révén szerzi meg, ''termikusan aktivált folyamatok''nak nevezik. Ezen jelenségek tanulmányozása lehetőséget ad e két állandó arányának ($e/k$) meghatározására. Magával ezzel az aránnyal is gyakran találkozunk, de emellett arra is felhasználhatjuk, hogy az egyik állandó és az arány ismeretében a másik állandó értékét ki-számítsuk.
+
Az elektron töltése ($e$) és a Boltzmann-állandó ($k$) fontos természeti állandók, amelyek ismeretére számos jelenség leírásánál szükségünk van. Az olyan folyamatokat, amelyeknek során pl. egy részecske a továbbhaladásához szükséges energiát a termikus mozgásból származó véletlen energiaközlés révén szerzi meg, ''termikusan aktivált folyamatok''nak nevezik. Ezen jelenségek tanulmányozása lehetőséget ad e két állandó arányának ($e/k$) meghatározására. Magával ezzel az aránnyal is gyakran találkozunk, de emellett arra is felhasználhatjuk, hogy az egyik állandó és az arány ismeretében a másik állandó értékét kiszámítsuk.
  
−
Félvezetőkben az elektromos áramot ''elektronok'' és ''lyukak'' (elektronhiányok) mozgása eredményezi. Bizonyos adalék anyagok (foszfor, arzén) hatására a félvezetőkben az elektronok any-nyira túlsúlyba kerülnek a lyukakhoz képest, hogy gyakorlatilag csak elektronvezetés alakul ki: az ilyen félvezetőt ''n típusú''nak nevezik. Más adalékok (bór, gallium, alumínium) viszont a félvezetőben lyukvezetést hoznak létre: az ilyen félvezetők a ''p típusú'' félvezetők.
+
Félvezetőkben az elektromos áramot ''elektronok'' és ''lyukak'' (elektronhiányok) mozgása eredményezi. Bizonyos adalék anyagok (foszfor, arzén) hatására a félvezetőkben az elektronok annyira túlsúlyba kerülnek a lyukakhoz képest, hogy gyakorlatilag csak elektronvezetés alakul ki: az ilyen félvezetőt ''n típusú''nak nevezik. Más adalékok (bór, gallium, alumínium) viszont a félvezetőben lyukvezetést hoznak létre: az ilyen félvezetők a ''p típusú'' félvezetők.
  
−
Ha egy ''p'' típusú és egy ''n'' típusú félvezetőt érintkezésbe hozunk (ez az ún. ''p–n átmenet''), akkor az érintkezési helyen kontaktpotenciál jön létre, mert energetikai okok miatt az ''n'' típusú részből elektronok mennek át a ''p'' típusú részbe (így az negatív többlettöltésre tesz szert), a ''p'' típusú részből viszont lyukak mennek át az ''n'' típusú részbe (így abban pozitív többlettöltés jön létre). A kontaktus létrejöttének pillanatában te-hát egy, a ''p'' rétegből az ''n'' rétegbe irányuló kezdeti áram folyik. Az áram hatására a potenciálkülönbség nő, ami egyre jobban akadályozza a további töltésátmenetet, ezért egy bizonyos feszültség elérése után a ''p→n'' irányú áram megszűnik, és kialakul egy állandósult kontaktpotenciál. Ezzel egyidejűleg a kontaktus két oldalán létrejön egy olyan tartomány, amelyben nincsenek mozgásképes töltéshordozók. A töltés-hordozók áthaladását (a ''p→n'' irányú áramot) ezen a kiürített tartományon át a létrejött $U_D$  magasságú potenciálgát akadályozza, ezért külső feszültség nélkül a töltéshordozók csak a termikus mozgás segítségével, véletlenszerűen jutnak át.
+
Ha egy ''p'' típusú és egy ''n'' típusú félvezetőt érintkezésbe hozunk (ez az ún. ''p–n átmenet''), akkor az érintkezési helyen kontaktpotenciál jön létre, mert energetikai okok miatt az ''n'' típusú részből elektronok mennek át a ''p'' típusú részbe (így az negatív többlettöltésre tesz szert), a ''p'' típusú részből viszont lyukak mennek át az ''n'' típusú részbe (így abban pozitív többlettöltés jön létre). A kontaktus létrejöttének pillanatában tehát egy, a ''p'' rétegből az ''n'' rétegbe irányuló kezdeti áram folyik. Az áram hatására a potenciálkülönbség nő, ami egyre jobban akadályozza a további töltésátmenetet, ezért egy bizonyos feszültség elérése után a ''p→n'' irányú áram megszűnik, és kialakul egy állandósult kontaktpotenciál. Ezzel egyidejűleg a kontaktus két oldalán létrejön egy olyan tartomány, amelyben nincsenek mozgásképes töltéshordozók. A töltéshordozók áthaladását (a ''p→n'' irányú áramot) ezen a kiürített tartományon át a létrejött $U_D$  magasságú potenciálgát akadályozza, ezért külső feszültség nélkül a töltéshordozók csak a termikus mozgás segítségével, véletlenszerűen jutnak át.
  
 
Eléggé általánosan igaz, hogy a termikusan aktivált folyamat gyakorisága az <math>e^{- \frac{E}{k T} }</math> faktorral arányos, ahol $E$ a továbbhaladáshoz szükséges energia, $k$ a Boltzmann-állandó, $T$ pedig az abszolút hőmérséklet. Ennek megfelelően annak gyakorisága, hogy egy lyuk ''p→n'' irányban vagy egy elektron ''n→p'' irányban az $U_D$ magasságú potenciálgáton átugrik, az $e^{- \frac{e U_D}{k T} }$ faktorral arányos ($e$ az elektron töltésének nagysága). Ez egyben azt is jelenti, hogy a termikus aktiváció segítségével a potenciálgáton át egy ''p→n'' irányú, ún. injektált áram folyik:
 
Eléggé általánosan igaz, hogy a termikusan aktivált folyamat gyakorisága az <math>e^{- \frac{E}{k T} }</math> faktorral arányos, ahol $E$ a továbbhaladáshoz szükséges energia, $k$ a Boltzmann-állandó, $T$ pedig az abszolút hőmérséklet. Ennek megfelelően annak gyakorisága, hogy egy lyuk ''p→n'' irányban vagy egy elektron ''n→p'' irányban az $U_D$ magasságú potenciálgáton átugrik, az $e^{- \frac{e U_D}{k T} }$ faktorral arányos ($e$ az elektron töltésének nagysága). Ez egyben azt is jelenti, hogy a termikus aktiváció segítségével a potenciálgáton át egy ''p→n'' irányú, ún. injektált áram folyik:
−
{{eq| I_I {{=}} C_0 e^{-\frac{e U_D}{kT} } |eq:1| (1) }}
+
{{eq| I_I {{=}} C e^{-\frac{e U_D}{kT} } |eq:1| (1) }}
−
A kiürített tartományon át ugyanakkor létrjön egy ellenkező irányú áram is, ami annak kö-vetkezménye, hogy a termikus mozgás (termikus aktiváció) révén, ha kis számban is, de mindig keletkeznek töltéshordozók, így – többek között – a kiürített réteg ''n'' oldalán lyukak, ''p'' oldalán pedig elektronok jelennek meg. Mivel a kontaktpotenciál ezeknek a mozgását a kontaktuson át éppen elősegíti, ily módon egy ''n→p'' irányú, ún. ''telítési (szaturációs) áram'', <math>I_s</math> jön létre. Ez az áram nem függ a kontaktuson kialakult feszültségtől, csak a termikusan keltett töltéshordozók mennyiségétől. Külső feszültség nélküli (egyensúlyi) állapotban a két áram egymást kiegyenlíti, vagyis ekkor $I_I {{=}} I_s$.
+
A kiürített tartományon át ugyanakkor létrjön egy ellenkező irányú áram is, ami annak következménye, hogy a termikus mozgás (termikus aktiváció) révén, ha kis számban is, de mindig keletkeznek töltéshordozók, így – többek között – a kiürített réteg ''n'' oldalán lyukak, ''p'' oldalán pedig elektronok jelennek meg. Mivel a kontaktpotenciál ezeknek a mozgását a kontaktuson át éppen elősegíti, ily módon egy ''n→p'' irányú, ún. ''telítési (szaturációs) áram'', <math>I_s</math> jön létre. Ez az áram nem függ a kontaktuson kialakult feszültségtől, csak a termikusan keltett töltéshordozók mennyiségétől. Külső feszültség nélküli (egyensúlyi) állapotban a két áram egymást kiegyenlíti, vagyis ekkor $I_I {{=}} I_s$.
  
 
Ha a ''p–n'' átmenetre $U$ külső feszültséget kapcsolunk, akkor ez módosítja a potenciálgát magasságát, ezért megváltoztatja az injektált áramot, amely most
 
Ha a ''p–n'' átmenetre $U$ külső feszültséget kapcsolunk, akkor ez módosítja a potenciálgát magasságát, ezért megváltoztatja az injektált áramot, amely most
31. sor: 31. sor:
 
amivel az injektált áramra azt kapjuk, hogy
 
amivel az injektált áramra azt kapjuk, hogy
 
{{eq| I_I{{=}}I_se^{\frac{eU}{kT} }. |eq:4| (4) }}
 
{{eq| I_I{{=}}I_se^{\frac{eU}{kT} }. |eq:4| (4) }}
−
A kontaktuson átfolyó $I$ eredő áram a feszült-ségfüggő $I_I$ injektált áram és a feszültségtől független $I_S$ telítési áram különbsége:
+
A kontaktuson átfolyó $I$ eredő áram a feszültségfüggő $I_I$ injektált áram és a feszültségtől független $I_S$ telítési áram különbsége:
 
{{eq| I{{=}}I_s\left(e^{\frac{eU}{kt} }-1 \right). |eq:5| (5) }}
 
{{eq| I{{=}}I_s\left(e^{\frac{eU}{kt} }-1 \right). |eq:5| (5) }}
 
Ez az összefüggés azt az ismert tapasztalatot tükrözi, hogy egy ilyen kontaktus különböző irányban előfeszítve különböző nagyságú áramot bocsát át, más szóval ''egyenirányít''. Az ilyen egyenirányító ''p–n'' átmenetet ''félvezető diódá''nak nevezik.
 
Ez az összefüggés azt az ismert tapasztalatot tükrözi, hogy egy ilyen kontaktus különböző irányban előfeszítve különböző nagyságú áramot bocsát át, más szóval ''egyenirányít''. Az ilyen egyenirányító ''p–n'' átmenetet ''félvezető diódá''nak nevezik.
37. sor: 37. sor:
 
==A mérési módszer==
 
==A mérési módszer==
  
−
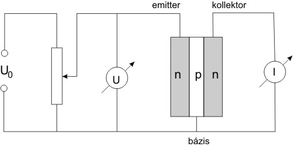
A mérés során egy félvezető eszközben az ([[#eq:5|5]]) egyenlettel leírható áram-feszültség összefüggést (ún. áram–feszültség karakterisztikát) mérünk ki, és az exponensben szereplő kifejezés kiértékelésével meghatározzuk az $e/k$ arányt. A mérés könnyebben megvalósítható, ha nem közvetlenül dióda-karakterisztikát vizsgálunk, hanem az [[#fig:1|1.ábrán]] látható elrendezésben egy tranzisztor kollektor¬áramának ($I$) a bázis–emitter feszültség-től ($U$) való függését vizsgáljuk, amely ugyancsak az ([[#eq:5|5]]) egyenlettel írható le (a tranzisztor – mint az ábrán is látható – lényegében két egymáshoz kapcsolt félvezető dióda).
+
A mérés során egy félvezető eszközben az ([[#eq:5|5]]) egyenlettel leírható áram-feszültség összefüggést (ún. áram–feszültség karakterisztikát) mérünk ki, és az exponensben szereplő kifejezés kiértékelésével meghatározzuk az $e/k$ arányt. A mérés könnyebben megvalósítható, ha nem közvetlenül dióda-karakterisztikát vizsgálunk, hanem az [[#fig:1|1.ábrán]] látható elrendezésben egy tranzisztor kollektor-áramának ($I$) a bázis–emitter feszültségtől ($U$) való függését vizsgáljuk, amely ugyancsak az ([[#eq:5|5]]) egyenlettel írható le (a tranzisztor – mint az ábrán is látható – lényegében két egymáshoz kapcsolt félvezető dióda).
  
 
<span id="fig:1">[[Fájl:Tranzisztor kapcsolása.bmp|közép|bélyegkép|300px|1.ábra: a dióda karakterisztikájának a meghatározásához használt áramkör]]</span>
 
<span id="fig:1">[[Fájl:Tranzisztor kapcsolása.bmp|közép|bélyegkép|300px|1.ábra: a dióda karakterisztikájának a meghatározásához használt áramkör]]</span>
  
−
Az [[#eq:5|(5)]] alakú karakterisztikából az $e/k$ hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy <math>e^{\frac{eU}{kT} }</math>, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége $100meV$ nagyságrendű. Ezért jó közelítéssel ér-vényes, hogy
+
Az [[#eq:5|(5)]] alakú karakterisztikából az $e/k$ hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy <math>e^{\frac{eU}{kT} }</math>, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége $100meV$ nagyságrendű. Ezért jó közelítéssel érvényes, hogy
 
{{eq| I{{=}}I_se^{\frac{eU}{kt} }. |eq:6| (6) }}
 
{{eq| I{{=}}I_se^{\frac{eU}{kt} }. |eq:6| (6) }}
−
Ha az egyenlet mindkét oldalának a termé-szetes alapú logaritmusát vesszük, akkor az $I–U$ összefüggés linearizálható, hiszen
+
Ha az egyenlet mindkét oldalának a természetes alapú logaritmusát vesszük, akkor az $I–U$ összefüggés linearizálható, hiszen
 
{{eq|ln I {{=}}ln I_s+\frac{e}{kT}U. |eq:7| (7)}}
 
{{eq|ln I {{=}}ln I_s+\frac{e}{kT}U. |eq:7| (7)}}
−
Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük a kollektoráramot különböző bázis–emitter feszültségeknél, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pon-tok egy egyenest adnak. Jelölje a mérési pon-tokhoz illesztett egyenes meredekségét $M_U$.
+
Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük a kollektoráramot különböző bázis–emitter feszültségeknél, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pontok egy egyenest adnak. Jelölje a mérési pontokhoz illesztett egyenes meredekségét $M_U$.
 
{{eq| M_U{{=}}\frac{e}{kT} |eq:8| (8)}}
 
{{eq| M_U{{=}}\frac{e}{kT} |eq:8| (8)}}
 
összefüggés, amiből az $e/k$ hányadosra azt kapjuk, hogy
 
összefüggés, amiből az $e/k$ hányadosra azt kapjuk, hogy
59. sor: 59. sor:
 
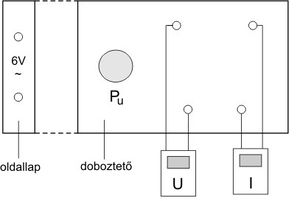
A mérés az [[#fig:1|1.ábrán]] már bemutatott áramkörben történik. Az áramkör és az egyenfeszültséget adó tápegység egy átlátszó műanyag dobozban található, amelyhez a tápfeszültséget az oldallapján levő csatlakozó hüvelyekre kapcsolt 8 V-os egyenfeszültséggel biztosítjuk ([[#fig:2|2]]-[[#fig:3|3.ábrán]]). Az $I$ kollektoráram és az $U$ bázis–emitter feszültség mérésére szolgáló műszereket a doboz ''tetején'' található hüvelyekhez csatlakoztatjuk, az $U$ feszültséget a P<sub>u</sub> potenciométerrel változtatjuk.
 
A mérés az [[#fig:1|1.ábrán]] már bemutatott áramkörben történik. Az áramkör és az egyenfeszültséget adó tápegység egy átlátszó műanyag dobozban található, amelyhez a tápfeszültséget az oldallapján levő csatlakozó hüvelyekre kapcsolt 8 V-os egyenfeszültséggel biztosítjuk ([[#fig:2|2]]-[[#fig:3|3.ábrán]]). Az $I$ kollektoráram és az $U$ bázis–emitter feszültség mérésére szolgáló műszereket a doboz ''tetején'' található hüvelyekhez csatlakoztatjuk, az $U$ feszültséget a P<sub>u</sub> potenciométerrel változtatjuk.
  
−
<span id="fig:2">[[Fájl:Aramkor.jpg|közép|bélyegkép|300px|2.ábra: a mérés során hasznát áramkör]]</span>
+
{|
−
 
+
| <span id="fig:2">[[Fájl:Aramkor.jpg|közép|bélyegkép|300px|2.ábra: a mérés során hasznát áramkör]]</span>
−
<span id="fig:3">[[Fájl:aramkor2.jpg|közép|bélyegkép|300px|3.ábra: az mérési elrendezés fényképen]]</span>
+
| <span id="fig:3">[[Fájl:eperk2.jpg|közép|bélyegkép|x280px|3.a ábra: : A vizsgált tranzisztort és a kapcsolódó elektronikát tartalmazó mérődoboz.]]</span>
 +
|[[Fájl:eperk1.jpg|közép|bélyegkép|x280px|3.b ábra: A mérési összeállítás a termosztáttal és a vizsgált tranzisztort tartalmazó dobozzal.]]
 +
|}
  
 
Mivel az áram erősen függ a hőmérséklettől, a mérésnél a hőmérséklet állandó értéken tartásáról külön gondoskodni kell. A vizsgált tranzisztort tartó alumínium tömbön ezért termosztáttal stabilizált hőmérsékletű vizet áramoltatunk át. A tranzisztor hőmérséklete jó közelítéssel a víz hőmérsékletével egyezik meg, amelyet a termosztát hőmérőjével mérünk. A víz hőmérsékletét a termosztáton található kontakthőmérő segítségével állíthatjuk a kívánt értékre.
 
Mivel az áram erősen függ a hőmérséklettől, a mérésnél a hőmérséklet állandó értéken tartásáról külön gondoskodni kell. A vizsgált tranzisztort tartó alumínium tömbön ezért termosztáttal stabilizált hőmérsékletű vizet áramoltatunk át. A tranzisztor hőmérséklete jó közelítéssel a víz hőmérsékletével egyezik meg, amelyet a termosztát hőmérőjével mérünk. A víz hőmérsékletét a termosztáton található kontakthőmérő segítségével állíthatjuk a kívánt értékre.
67. sor: 69. sor:
  
 
==Mérési feladatok==
 
==Mérési feladatok==
−
*1. Kb.''0.4V-0.5V'' között ''20mV''-onként változtatva a bázis–emitter feszültséget, vegye fel az áram–feszültség karakterisztikát 30ºC-on! Ügyeljen arra, hogy a feszültséggel semmiképp ne lépje túl az ''1V'' értéket!  Ezután attól a tartománytól kezdve, ahonnan (az exponenciális jelleg miatt) az áram láthatóan gyorsan változik (''0.5V'' környékén várható), sűrítse a mérési pontokat   távolságra! A mérést a potenciométer által behatárolt teljes feszültségtartományban végezze el.Ismételje meg a mérést 45, 60, 70, 80 ºC-on ! (A felfűtés után várja ki, amíg a termosztát néhányszori ki-be kapcsolása után biztosan stabilizálódott a tranzisztor hőmérséklete.)
+
*1. Kb.''0.4V-0.5V'' között ''20mV''-onként változtatva a bázis–emitter feszültséget, vegye fel az áram–feszültség karakterisztikát 30ºC-on! Ügyeljen arra, hogy a feszültséggel semmiképp ne lépje túl az ''1V'' értéket!  Ezután attól a tartománytól kezdve, ahonnan (az exponenciális jelleg miatt) az áram láthatóan gyorsan változik (''0.5V'' környékén várható), sűrítse a mérési pontokat! <br />
 +
''Nagyságrendileg mekkora áramokat vár a 0,4V-0,5V intervallumban és mekkorát 0,6 V körül?''<br />
 +
A mérést a potenciométer által behatárolt teljes feszültségtartományban végezze el.Ismételje meg a mérést 45, 60, 70, 80 ºC-on ! (A felfűtés után várja ki, amíg a termosztát néhányszori ki-be kapcsolása után biztosan stabilizálódott a tranzisztor hőmérséklete.)
 +
A mérésnél használt multiméter bekapcsolás után automatikus méréshatár üzemmódba áll be. Kis nyitófeszültségnél ez előnyös, mert az ilyenkor folyó nA nagyságrendű áramot is elég pontosan lehet mérni. A dióda nyitása során viszont jelentősen nő az áram, a műszer automatikusan átkapcsol nagyobb mérési tartományba. Mivel a mérőműszer nem ideális, ilyenkor változik a belső ellenállása is!!! Ekkor már a dióda ellenállása is elég kicsi.A két jelenség együttesen azt eredményezi, hogy a mért áram menetében törés keletkezik. Ezt úgy lehet elkerülni,hogy a mérés elején megnézzük, hogy teljes nyitófeszültségnél mekkora áram folyik (a feszültségállító potenciométert az óramutató járásával megegyezően szélső állásba forgatjuk). Az ehhez az áramhoz tartozó optimális méréshatárt állítjuk be a kézi méréshatár állítás üzemmódban. Így a mérés elején kisebb felbontásban mérjük az áramot, de ez nem növeli a mérés hibáját.
  
−
*2. A kapott adatokat ábrázolja az $lnI-U$ grafikonon, illesszen egyenest a pontokra, és hatá-rozza meg az egyenesek meredekségét!
+
*2. A kapott adatokat ábrázolja az $lnI-U$ grafikonon, illesszen egyenest a pontokra, és határozza meg az egyenesek meredekségét!
  
−
*3. A meredekségek mindegyikéből határozza meg az $e/k$ hányadost, átlagolja a kapott ér-tékeket, és becsülje meg a mérés hibáját!
+
*3. A meredekségek mindegyikéből határozza meg az $e/k$ hányadost, átlagolja a kapott értékeket, és becsülje meg a mérés hibáját!
  
 
*4. Számolja ki $I_s$ értékeit és ábrázolja az $I_s-T$ grafikont!
 
*4. Számolja ki $I_s$ értékeit és ábrázolja az $I_s-T$ grafikont!
  
−
==PDF formátum==
+
==Irodalom==
 +
'''Aldert van der  Ziel: Szilárdtest elektronika, Műszaki Könyvkiadó, 1982'''
 +
 
 +
 
 +
 
 +
=A Planck- és a Boltzmann-állandók hányadosának mérése=
 +
 
 +
''A mérés célja:''
 +
*Elemi fizikai állandók arányának megállapítása, a hőmérsékleti sugárzás törvényeinek alkalmazása.
 +
 
 +
''Ennek érdekében :''
 +
*Megvizsgáljuk egy izzólámpa sugárzásának spektrális eloszlását a volfrámszál hőmérsékletének függvényében.
 +
 
 +
Ismételje át a [[Hőmérsékleti sugárzás vizsgálata]] c. mérés elméleti anyagát. Az alábbiakban annak csak rövid kivonatát ismertetjük.
 +
 
 +
==Elméleti összefoglaló==
 +
 
 +
Valamely test ''a'' abszorpcióképessége a testre eső sugárzási energiának az a tört része, amelyet a test elnyel (nem ereszt át, nem ver vissza). (Hasonló módon definiálható a ''d'' áteresztő- és az ''r'' reflektálóképesség.  ) A test ''e'' emisszió képességén a test felületének 1 cm<sup>2</sup>-es darabja által 1 s alatt az egységnyi térszögben, a felület normálisának irányában kibocsátott fényenergiát értjük.
 +
 
 +
Mind ''a'', mint ''e'' a $T$ hőmérsékleten és a ''λ'' hullámhosszon kívül nagy mértékben függ a test különböző sajátosságaitól. Azt az ideális testet, amely a rá eső bármely hullámhosszúságú sugárzást teljesen elnyeli, abszolút fekete testnek hívjuk. Ennek abszorpcióképessége tehát $A$ = 1, emisszió képességét pedig jelöljük $E$-vel.
 +
 
 +
Az $e/a$ viszony minden testnél ugyanaz, és csak ''λ''-nak és $T$-nek a függvénye:
 +
$\frac{e}{a} {{=}} \frac{E}{A} {{=}} E(\lambda,T)$
 +
 
 +
Az $E(\lambda,T)$ kifejezés tehát megadja a fekete  test által kisugárzott energia hullámhossz szerinti eloszlását a hőmérséklet függvényében. Ez Kirchhoff törvénye. Kiemeljük, hogy a törvény nemcsak az összes sugárzásra, hanem minden egyes hullámhosszra igaz.
 +
 
 +
A fekete test $E(\lambda,T)$ hőmérséklet- és hullámhosszfüggését a Planck-féle sugárzási törvény adja meg:
 +
{{eq| E(\lambda)d\lambda {{=}}2c^{2}h\frac{ \lambda^{-5} }{e^{\frac{ch}{\lambda k T} } -1} d\lambda  |eq:11| (1)}}
 +
ahol
 +
*''c'' a fény sebessége,
 +
*''λ'' a hullámhossz,
 +
*''k'' a Boltzmann-állandó,
 +
*''T'' a sugárzó test abszolút hőmérséklete.
 +
A kifejezés jelentése: a fekete test által kisugárzott energia értéke adott hőmérsékleten a $\lambda+d\lambda$,  hullámhossz intervallumban. A fekete test sugárzását leíró összefüggések nem tartalmaznak semmilyen anyagi állandót, ezért az abszolút fekete test a sugárzások mérésének sugárforrás-standardja. Az abszolút fekete test gyakorlati megvalósításának nehézségei és nehezen mérhető spektrális eloszlása miatt az abszolút fekete test helyett sztenderd volfrámszálas lámpát szokás használni.
 +
 
 +
Esetünkben a volfrám hőmérsékleti sugárzásának energia eloszlását az alábbi megfontolások alapján adhatjuk meg:
 +
 
 +
A mérésben előforduló  hőmérsékleti sávban (300 K- 3000 K) a Planck-féle sugárzási törvény ( [[#eq:11|(1)]] -es képlet) nevezőjében szereplő „1” elhanyagolható, és így ez a Wien-féle közelítésbe megy át:
 +
{{eq| E(\lambda)d\lambda {{=}} 2c^{2}h\lambda^{-5}e^{-\frac{ch}{\lambda kT} }d\lambda |eq:12| (2)}}
 +
Felhasználva, hogy
 +
{{eq| e(\lambda,T){{=}}a(\lambda,T)E(\lambda,T),  |eq:13| (3) }}
 +
{{eq| e_\lambda d\lambda {{=}} a(\lambda,T)2c^{2}h\lambda^{-5}e^{\frac{ch}{\lambda kT} }  |eq:14| (4) }}
 +
ahol $a(\lambda,T)$ a volfrám abszorpcióképessége Ez 1000 és 1800 ºC között jó közelítéssel állandónak vehető a mérésben használt hullámhosszak esetén.
 +
 
 +
==A mérés elve==
 +
 
 +
Egy volfrámsugárzó $\lambda+d\lambda$ hullámhossztartományba eső $I_\lambda (T)$ intenzitása [[#eq:14|(4)]] alapján a következő:
 +
{{eq| I:\lambda(T) {{=}} C_\lambda a(\lambda,T)2c^{2}h\lambda^{-5}e^{\frac{ch}{\lambda kT} }  |eq:15| (5) }}
 +
ahol $C_\lambda$ az arányossági tényező.
 +
Az [[#eq:15|(5)]] összefüggés mindkét oldalának természetes alapú logaritmusát véve:
 +
{{eq| ln I_\lambda (T) {{=}} A-\frac{B}{T} |eq:16| (6) }}
 +
ahol
 +
{{eq| A {{=}} ln C_\lambda a(\lambda,T)2c^{2}h\lambda^{-5}, |eq:17| (7) }}
 +
{{eq| B {{=}} \frac{ch}{k\lambda}  |eq:18|  (8) }}
 +
A volfrámizzó fényéből kiszűrt, adott színű fény intenzitását és a szál hőmérsékletét mérve, a kapott adatokból az $ln I_\lambda -\frac{1}{T}$ egyenes meredekségét meghatározva, ''λ'' ismeretében lehet a $\frac{h}{k}$ értékét kiszámítani.
 +
 
 +
Az izzószál hőmérsékletét az átfolyó áram és a rajta eső feszültség mérésével, ellenállásának kiszámításával az alábbi, a mérési tartományunkban érvényes közelítő polinom segítségével állapítjuk meg:
 +
$ T =101,86399+216,12572\left(\frac{R_T}{R_300}\right)-3,15479\left(\frac{R_T}{R_300}\right)^{2}+0,04911\left(\frac{R_T}{R_300}\right)^{3}$
 +
 
 +
==A méréshez használt eszközök==
 +
*volfrámszálas izzólámpa 12 V, 35W, (lámpaházban, kivezetésekkel), optikai padon csúsztatható
 +
*4 színszűrő optikai padra erősítve
 +
*OHMEG ST-255 tápegység
 +
*2 db HAMEG multiméter
 +
*GOM-802 milliohm-mérő
 +
*Fényintenzitás-mérő (Luxmérő)Voltcraft MS-1300
 +
 
 +
{|
 +
| [[Fájl:hperk1.jpg|közép|bélyegkép|x250px|A mérési összeállítás.]]
 +
| [[Fájl:hperk2.jpg|közép|bélyegkép|x250px|A fénymérő]]
 +
| [[Fájl:hperk3.jpg|közép|bélyegkép|x250px| A fényforrás, a színszűrők és fénymérő (takarásban).]]
 +
|}
 +
 
 +
A színszűrők hullámhossz-adatai:
 +
Sárga: 570±60 nm
 +
Narancs: 650±90 nm
 +
Zöld: 540±40 nm
 +
Kék: 470±60 nm
 +
 
 +
==Mérési feladatok==
 +
 
 +
*1. Mérje meg az izzó hidegellenállását! A lámpaház végénél a vezetékeken levő két banánhüvelyt kösse össze a GOM-802 milliohm-mérővel (négyhuzalos ellenállásmérés!), a leolvasott érték az izzó hideg ellenállása. Ügyeljen arra, hogy a csatlakozások biztos kontaktust adjanak. Ne felejtse el feljegyezni a laboratórium hőmérsékletét!
 +
*2. A lámpát árammérő közbeiktatásával kösse rá a tápegységre, és a lámpaház mögötti két banánhüvelyen mérje az izzón eső feszültséget! Győződjön meg arról, hogy a tápegység kimeneti feszültsége 0V-ra van állítva, majd kapcsolja be a tápegységet! A tápegység feszültségének szabályozásával az izzón eső feszültséget állítsa 2 V-ra. Ezt az értéket jegyezze fel az izzón átfolyó árammal együtt! Tolja az izzót és a fénymérőt tartalmazó állványt egymás után az egyes színszűrőkhöz, és olvassa le mindegyiknél a fénymérő által jelzett értéket. A fénymérő lux-ban (fotometriai mértékegység)méri a fényintenzitást, de a számértékére nem lesz szükségünk, mivel csak a logaritmált  függvény meredekségét vizsgáljuk.
 +
*3. Végezze el a 2. feladatot az izzón eső feszültség 12 V-ig, voltonként való növelése mellett. Minden feszültség beállításnál olvassa le az izzón átfolyó áramot is, és ebből számolja az ellenállást Ohm törvényével! Így mind a négy színhez kap egy $I_\lambda–T$ adatsort.
 +
* ''Mit vár, a szűrőkön áthaladó sugárzások intenzitásai hogyan aránylanak egymáshoz? Az adatok elemzése alátámasztja-e ezt a várakozást. Ha nem, akkor mi lehet a magyarázata az eltérésnek?''
 +
*4. Ábrázolja mind a négy színszűrő esetében az $ln I_\lambda$ adatokat $\frac{1}{T}$ függvényében. Illesszen a pontokra egyenest, és a színszűrők hullámhossz-adatai alapján az egyenesek meredekségéből számítsa ki $\frac{h}{k}$ értékét mind a négy esetben. Számítsa ki ezek átlagát, és vesse össze eredményét a $\frac{h}{k}$ arány irodalmi értékével.
 +
 
 +
A mérés folyamán ügyeljen arra, hogy az izzóra ne jusson 12V-nál nagyobb feszültség!
 +
(A mérőszoba teljes besötétítésével biztosítsa, hogy a fénymérőbe csak az izzó fénye jusson!)
 +
 
 +
==Irodalom==
 +
'''Budó Ágoston–Mátrai Tibor: Kísérleti fizika III.  304-307.§.'''
 +
 
 +
'''A hőmérsékleti sugárzás vizsgálata c. mérés leírása '''
 +
 
 +
=PDF formátum=
 
*[[Media:E_per_k_2011_02_07.pdf|Az elektron töltése és a Boltzmann-állandó hányadosának (e/k) mérése]]
 
*[[Media:E_per_k_2011_02_07.pdf|Az elektron töltése és a Boltzmann-állandó hányadosának (e/k) mérése]]
 +
*[[Media:H_per_k_2011_02_07.pdf|A Planck és a Boltzmann-állandó hányadosának (h/k) mérése]]

A lap jelenlegi, 2014. április 24., 09:53-kori változata




Tartalomjegyzék


Az elektron töltése és a Boltzmann-állandó hányadosának (e/k) mérése

A mérés célja:

  • termikusan aktivált folyamat tanulmányozása félvezető p–n átmenetben,
  • az arány meghatározása.

Ennek érdekében:

  • összefoglaljuk a p–n átmeneten folyó áramra vonatkozó elméleti alapismereteket,(a jelenségek igen részletes leírása a megadott irodalomban olvasható),
  • kimérjük egy tranzisztor kollektor-áramának a bázis–emitter feszültségtől való függését, és meghatározzuk az arányt.

Elméleti összefoglaló

Az elektron töltése (\setbox0\hbox{$e$}% \message{//depth:\the\dp0//}% \box0%) és a Boltzmann-állandó (\setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0%) fontos természeti állandók, amelyek ismeretére számos jelenség leírásánál szükségünk van. Az olyan folyamatokat, amelyeknek során pl. egy részecske a továbbhaladásához szükséges energiát a termikus mozgásból származó véletlen energiaközlés révén szerzi meg, termikusan aktivált folyamatoknak nevezik. 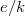Ezen jelenségek tanulmányozása lehetőséget ad e két állandó arányának (\setbox0\hbox{$e/k$}% \message{//depth:\the\dp0//}% \box0%) meghatározására. Magával ezzel az aránnyal is gyakran találkozunk, de emellett arra is felhasználhatjuk, hogy az egyik állandó és az arány ismeretében a másik állandó értékét kiszámítsuk.

Félvezetőkben az elektromos áramot elektronok és lyukak (elektronhiányok) mozgása eredményezi. Bizonyos adalék anyagok (foszfor, arzén) hatására a félvezetőkben az elektronok annyira túlsúlyba kerülnek a lyukakhoz képest, hogy gyakorlatilag csak elektronvezetés alakul ki: az ilyen félvezetőt n típusúnak nevezik. Más adalékok (bór, gallium, alumínium) viszont a félvezetőben lyukvezetést hoznak létre: az ilyen félvezetők a p típusú félvezetők.

Ha egy p típusú és egy n típusú félvezetőt érintkezésbe hozunk (ez az ún. p–n átmenet), akkor az érintkezési helyen kontaktpotenciál jön létre, mert energetikai okok miatt az n típusú részből elektronok mennek át a p típusú részbe (így az negatív többlettöltésre tesz szert), a p típusú részből viszont lyukak mennek át az n típusú részbe (így abban pozitív többlettöltés jön létre). A kontaktus létrejöttének pillanatában tehát egy, a p rétegből az n rétegbe irányuló kezdeti áram folyik. Az áram hatására a potenciálkülönbség nő, ami egyre jobban akadályozza a további töltésátmenetet, ezért egy bizonyos feszültség elérése után a p→n irányú áram megszűnik, és kialakul egy állandósult kontaktpotenciál. Ezzel egyidejűleg a kontaktus két oldalán létrejön egy olyan tartomány, amelyben nincsenek mozgásképes töltéshordozók. A töltéshordozók áthaladását (a p→n irányú áramot) ezen a kiürített tartományon át a létrejött 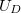\setbox0\hbox{$U_D$}% \message{//depth:\the\dp0//}% \box0% magasságú potenciálgát akadályozza, ezért külső feszültség nélkül a töltéshordozók csak a termikus mozgás segítségével, véletlenszerűen jutnak át.

Eléggé általánosan igaz, hogy a termikusan aktivált folyamat gyakorisága az 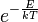e^{- \frac{E}{k T} } faktorral arányos, ahol \setbox0\hbox{$E$}% \message{//depth:\the\dp0//}% \box0% a továbbhaladáshoz szükséges energia, \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% a Boltzmann-állandó, \setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0% pedig az abszolút hőmérséklet. 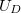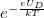Ennek megfelelően annak gyakorisága, hogy egy lyuk p→n irányban vagy egy elektron n→p irányban az \setbox0\hbox{$U_D$}% \message{//depth:\the\dp0//}% \box0% magasságú potenciálgáton átugrik, az \setbox0\hbox{$e^{- \frac{e U_D}{k T} }$}% \message{//depth:\the\dp0//}% \box0% faktorral arányos (\setbox0\hbox{$e$}% \message{//depth:\the\dp0//}% \box0% az elektron töltésének nagysága). Ez egyben azt is jelenti, hogy a termikus aktiváció segítségével a potenciálgáton át egy p→n irányú, ún. injektált áram folyik:

 
\[ I_I = C e^{-\frac{e U_D}{kT} } \]
(1)

A kiürített tartományon át ugyanakkor létrjön egy ellenkező irányú áram is, ami annak következménye, hogy a termikus mozgás (termikus aktiváció) révén, ha kis számban is, de mindig keletkeznek töltéshordozók, így – többek között – a kiürített réteg n oldalán lyukak, p oldalán pedig elektronok jelennek meg. Mivel a kontaktpotenciál ezeknek a mozgását a kontaktuson át éppen elősegíti, ily módon egy n→p irányú, ún. telítési (szaturációs) áram, 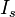I_s jön létre. Ez az áram nem függ a kontaktuson kialakult feszültségtől, csak a termikusan keltett töltéshordozók mennyiségétől. 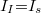Külső feszültség nélküli (egyensúlyi) állapotban a két áram egymást kiegyenlíti, vagyis ekkor \setbox0\hbox{$I_I {{=}} I_s$}% \message{//depth:\the\dp0//}% \box0%.

Ha a p–n átmenetre \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% külső feszültséget kapcsolunk, akkor ez módosítja a potenciálgát magasságát, ezért megváltoztatja az injektált áramot, amely most

 
\[ I_I = C e^{-\frac{e\left( U_D - U \right)}{kT} } \]
(2)

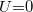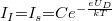Itt \setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0% állandó, az \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% feszültség pedig negatív, ha a feszültség a kontaktpotenciállal egyirányú, és pozitív, ha azzal ellentétes. Mivel \setbox0\hbox{$U {{=}} 0$}% \message{//depth:\the\dp0//}% \box0% esetén \setbox0\hbox{$I_I{{=}}I_s{{=}}Ce^{-\frac{eU_D}{kT} }$}% \message{//depth:\the\dp0//}% \box0%,

 
\[ C=I_se^{\frac{eU_D}{kT} }, \]
(3)

amivel az injektált áramra azt kapjuk, hogy

 
\[ I_I=I_se^{\frac{eU}{kT} }. \]
(4)

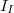A kontaktuson átfolyó \setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0% eredő áram a feszültségfüggő \setbox0\hbox{$I_I$}% \message{//depth:\the\dp0//}% \box0% injektált áram és a feszültségtől független 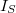\setbox0\hbox{$I_S$}% \message{//depth:\the\dp0//}% \box0% telítési áram különbsége:

 
\[ I=I_s\left(e^{\frac{eU}{kt} }-1 \right). \]
(5)

Ez az összefüggés azt az ismert tapasztalatot tükrözi, hogy egy ilyen kontaktus különböző irányban előfeszítve különböző nagyságú áramot bocsát át, más szóval egyenirányít. Az ilyen egyenirányító p–n átmenetet félvezető diódának nevezik.

A mérési módszer

A mérés során egy félvezető eszközben az (5) egyenlettel leírható áram-feszültség összefüggést (ún. áram–feszültség karakterisztikát) mérünk ki, és az exponensben szereplő kifejezés kiértékelésével meghatározzuk az 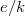\setbox0\hbox{$e/k$}% \message{//depth:\the\dp0//}% \box0% arányt. A mérés könnyebben megvalósítható, ha nem közvetlenül dióda-karakterisztikát vizsgálunk, hanem az 1.ábrán látható elrendezésben egy tranzisztor kollektor-áramának (\setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0%) a bázis–emitter feszültségtől (\setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0%) való függését vizsgáljuk, amely ugyancsak az (5) egyenlettel írható le (a tranzisztor – mint az ábrán is látható – lényegében két egymáshoz kapcsolt félvezető dióda).

1.ábra: a dióda karakterisztikájának a meghatározásához használt áramkör

Az (5) alakú karakterisztikából az 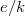\setbox0\hbox{$e/k$}% \message{//depth:\the\dp0//}% \box0% hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy 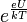e^{\frac{eU}{kT} }, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége 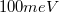\setbox0\hbox{$100meV$}% \message{//depth:\the\dp0//}% \box0% nagyságrendű. Ezért jó közelítéssel érvényes, hogy

 
\[ I=I_se^{\frac{eU}{kt} }. \]
(6)

Ha az egyenlet mindkét oldalának a természetes alapú logaritmusát vesszük, akkor az 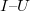\setbox0\hbox{$I–U$}% \message{//depth:\the\dp0//}% \box0% összefüggés linearizálható, hiszen

 
\[ln I =ln I_s+\frac{e}{kT}U. \]
(7)

Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük a kollektoráramot különböző bázis–emitter feszültségeknél, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pontok egy egyenest adnak. Jelölje a mérési pontokhoz illesztett egyenes meredekségét 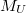\setbox0\hbox{$M_U$}% \message{//depth:\the\dp0//}% \box0%.

 
\[ M_U=\frac{e}{kT} \]
(8)

összefüggés, amiből az 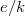\setbox0\hbox{$e/k$}% \message{//depth:\the\dp0//}% \box0% hányadosra azt kapjuk, hogy

 
\[ \frac{e}{k} =M_UT \]
(9)

A méréshez használt eszközök

  • MINISTAT 650 termosztát
  • HAMEG digitális multiméter
  • HAMEG hármas tápegység
  • Mérődoboz az alumínium tömbbe szerelt tranzisztorral és beállító elemekkel.

A mérőberendezés használata

A mérés az 1.ábrán már bemutatott áramkörben történik. Az áramkör és az egyenfeszültséget adó tápegység egy átlátszó műanyag dobozban található, amelyhez a tápfeszültséget az oldallapján levő csatlakozó hüvelyekre kapcsolt 8 V-os egyenfeszültséggel biztosítjuk (2-3.ábrán). Az \setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0% kollektoráram és az \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% bázis–emitter feszültség mérésére szolgáló műszereket a doboz tetején található hüvelyekhez csatlakoztatjuk, az \setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0% feszültséget a Pu potenciométerrel változtatjuk.

2.ábra: a mérés során hasznát áramkör
3.a ábra: : A vizsgált tranzisztort és a kapcsolódó elektronikát tartalmazó mérődoboz.
3.b ábra: A mérési összeállítás a termosztáttal és a vizsgált tranzisztort tartalmazó dobozzal.

Mivel az áram erősen függ a hőmérséklettől, a mérésnél a hőmérséklet állandó értéken tartásáról külön gondoskodni kell. A vizsgált tranzisztort tartó alumínium tömbön ezért termosztáttal stabilizált hőmérsékletű vizet áramoltatunk át. A tranzisztor hőmérséklete jó közelítéssel a víz hőmérsékletével egyezik meg, amelyet a termosztát hőmérőjével mérünk. A víz hőmérsékletét a termosztáton található kontakthőmérő segítségével állíthatjuk a kívánt értékre. A mérés a hőmérséklet beállításával kezdődik, az áram–feszültség mérését csak akkor kezdjük el, ha a hőmérséklet kellően stabilizálódott.

Mérési feladatok

  • 1. Kb.0.4V-0.5V között 20mV-onként változtatva a bázis–emitter feszültséget, vegye fel az áram–feszültség karakterisztikát 30ºC-on! Ügyeljen arra, hogy a feszültséggel semmiképp ne lépje túl az 1V értéket! Ezután attól a tartománytól kezdve, ahonnan (az exponenciális jelleg miatt) az áram láthatóan gyorsan változik (0.5V környékén várható), sűrítse a mérési pontokat!

Nagyságrendileg mekkora áramokat vár a 0,4V-0,5V intervallumban és mekkorát 0,6 V körül?
A mérést a potenciométer által behatárolt teljes feszültségtartományban végezze el.Ismételje meg a mérést 45, 60, 70, 80 ºC-on ! (A felfűtés után várja ki, amíg a termosztát néhányszori ki-be kapcsolása után biztosan stabilizálódott a tranzisztor hőmérséklete.) A mérésnél használt multiméter bekapcsolás után automatikus méréshatár üzemmódba áll be. Kis nyitófeszültségnél ez előnyös, mert az ilyenkor folyó nA nagyságrendű áramot is elég pontosan lehet mérni. A dióda nyitása során viszont jelentősen nő az áram, a műszer automatikusan átkapcsol nagyobb mérési tartományba. Mivel a mérőműszer nem ideális, ilyenkor változik a belső ellenállása is!!! Ekkor már a dióda ellenállása is elég kicsi.A két jelenség együttesen azt eredményezi, hogy a mért áram menetében törés keletkezik. Ezt úgy lehet elkerülni,hogy a mérés elején megnézzük, hogy teljes nyitófeszültségnél mekkora áram folyik (a feszültségállító potenciométert az óramutató járásával megegyezően szélső állásba forgatjuk). Az ehhez az áramhoz tartozó optimális méréshatárt állítjuk be a kézi méréshatár állítás üzemmódban. Így a mérés elején kisebb felbontásban mérjük az áramot, de ez nem növeli a mérés hibáját.

  • 2. A kapott adatokat ábrázolja az 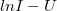\setbox0\hbox{$lnI-U$}% \message{//depth:\the\dp0//}% \box0% grafikonon, illesszen egyenest a pontokra, és határozza meg az egyenesek meredekségét!
  • 3. A meredekségek mindegyikéből határozza meg az 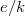\setbox0\hbox{$e/k$}% \message{//depth:\the\dp0//}% \box0% hányadost, átlagolja a kapott értékeket, és becsülje meg a mérés hibáját!
  • 4. Számolja ki 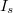\setbox0\hbox{$I_s$}% \message{//depth:\the\dp0//}% \box0% értékeit és ábrázolja az 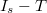\setbox0\hbox{$I_s-T$}% \message{//depth:\the\dp0//}% \box0% grafikont!

Irodalom

Aldert van der Ziel: Szilárdtest elektronika, Műszaki Könyvkiadó, 1982



A Planck- és a Boltzmann-állandók hányadosának mérése

A mérés célja:

  • Elemi fizikai állandók arányának megállapítása, a hőmérsékleti sugárzás törvényeinek alkalmazása.

Ennek érdekében :

  • Megvizsgáljuk egy izzólámpa sugárzásának spektrális eloszlását a volfrámszál hőmérsékletének függvényében.

Ismételje át a Hőmérsékleti sugárzás vizsgálata c. mérés elméleti anyagát. Az alábbiakban annak csak rövid kivonatát ismertetjük.

Elméleti összefoglaló

Valamely test a abszorpcióképessége a testre eső sugárzási energiának az a tört része, amelyet a test elnyel (nem ereszt át, nem ver vissza). (Hasonló módon definiálható a d áteresztő- és az r reflektálóképesség. ) A test e emisszió képességén a test felületének 1 cm2-es darabja által 1 s alatt az egységnyi térszögben, a felület normálisának irányában kibocsátott fényenergiát értjük.

Mind a, mint e a \setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0% hőmérsékleten és a λ hullámhosszon kívül nagy mértékben függ a test különböző sajátosságaitól. Azt az ideális testet, amely a rá eső bármely hullámhosszúságú sugárzást teljesen elnyeli, abszolút fekete testnek hívjuk. Ennek abszorpcióképessége tehát \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% = 1, emisszió képességét pedig jelöljük \setbox0\hbox{$E$}% \message{//depth:\the\dp0//}% \box0%-vel.

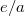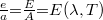
Az \setbox0\hbox{$e/a$}% \message{//depth:\the\dp0//}% \box0% viszony minden testnél ugyanaz, és csak λ-nak és \setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%-nek a függvénye: \setbox0\hbox{$\frac{e}{a} {{=}} \frac{E}{A} {{=}} E(\lambda,T)$}% \message{//depth:\the\dp0//}% \box0%

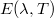Az \setbox0\hbox{$E(\lambda,T)$}% \message{//depth:\the\dp0//}% \box0% kifejezés tehát megadja a fekete test által kisugárzott energia hullámhossz szerinti eloszlását a hőmérséklet függvényében. Ez Kirchhoff törvénye. Kiemeljük, hogy a törvény nemcsak az összes sugárzásra, hanem minden egyes hullámhosszra igaz.

A fekete test 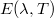\setbox0\hbox{$E(\lambda,T)$}% \message{//depth:\the\dp0//}% \box0% hőmérséklet- és hullámhosszfüggését a Planck-féle sugárzási törvény adja meg:

 
\[ E(\lambda)d\lambda =2c^{2}h\frac{ \lambda^{-5} }{e^{\frac{ch}{\lambda k T} } -1} d\lambda \]
(1)

ahol

  • c a fény sebessége,
  • λ a hullámhossz,
  • k a Boltzmann-állandó,
  • T a sugárzó test abszolút hőmérséklete.

A kifejezés jelentése: a fekete test által kisugárzott energia értéke adott hőmérsékleten a 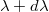\setbox0\hbox{$\lambda+d\lambda$}% \message{//depth:\the\dp0//}% \box0%, hullámhossz intervallumban. A fekete test sugárzását leíró összefüggések nem tartalmaznak semmilyen anyagi állandót, ezért az abszolút fekete test a sugárzások mérésének sugárforrás-standardja. Az abszolút fekete test gyakorlati megvalósításának nehézségei és nehezen mérhető spektrális eloszlása miatt az abszolút fekete test helyett sztenderd volfrámszálas lámpát szokás használni.

Esetünkben a volfrám hőmérsékleti sugárzásának energia eloszlását az alábbi megfontolások alapján adhatjuk meg:

A mérésben előforduló hőmérsékleti sávban (300 K- 3000 K) a Planck-féle sugárzási törvény ( (1) -es képlet) nevezőjében szereplő „1” elhanyagolható, és így ez a Wien-féle közelítésbe megy át:

 
\[ E(\lambda)d\lambda = 2c^{2}h\lambda^{-5}e^{-\frac{ch}{\lambda kT} }d\lambda \]
(2)

Felhasználva, hogy

 
\[ e(\lambda,T)=a(\lambda,T)E(\lambda,T), \]
(3)
 
\[ e_\lambda d\lambda = a(\lambda,T)2c^{2}h\lambda^{-5}e^{\frac{ch}{\lambda kT} } \]
(4)

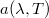ahol \setbox0\hbox{$a(\lambda,T)$}% \message{//depth:\the\dp0//}% \box0% a volfrám abszorpcióképessége Ez 1000 és 1800 ºC között jó közelítéssel állandónak vehető a mérésben használt hullámhosszak esetén.

A mérés elve

Egy volfrámsugárzó 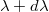\setbox0\hbox{$\lambda+d\lambda$}% \message{//depth:\the\dp0//}% \box0% hullámhossztartományba eső \setbox0\hbox{$I_\lambda (T)$}% \message{//depth:\the\dp0//}% \box0% intenzitása (4) alapján a következő:

 
\[ I:\lambda(T) = C_\lambda a(\lambda,T)2c^{2}h\lambda^{-5}e^{\frac{ch}{\lambda kT} } \]
(5)

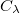ahol \setbox0\hbox{$C_\lambda$}% \message{//depth:\the\dp0//}% \box0% az arányossági tényező. Az (5) összefüggés mindkét oldalának természetes alapú logaritmusát véve:

 
\[ ln I_\lambda (T) = A-\frac{B}{T} \]
(6)

ahol

 
\[ A = ln C_\lambda a(\lambda,T)2c^{2}h\lambda^{-5}, \]
(7)
 
\[ B = \frac{ch}{k\lambda} \]
(8)

A volfrámizzó fényéből kiszűrt, adott színű fény intenzitását és a szál hőmérsékletét mérve, a kapott adatokból az 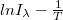\setbox0\hbox{$ln I_\lambda -\frac{1}{T}$}% \message{//depth:\the\dp0//}% \box0% egyenes meredekségét meghatározva, λ ismeretében lehet a 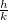\setbox0\hbox{$\frac{h}{k}$}% \message{//depth:\the\dp0//}% \box0% értékét kiszámítani.

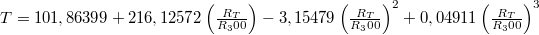
Az izzószál hőmérsékletét az átfolyó áram és a rajta eső feszültség mérésével, ellenállásának kiszámításával az alábbi, a mérési tartományunkban érvényes közelítő polinom segítségével állapítjuk meg: \setbox0\hbox{$ T =101,86399+216,12572\left(\frac{R_T}{R_300}\right)-3,15479\left(\frac{R_T}{R_300}\right)^{2}+0,04911\left(\frac{R_T}{R_300}\right)^{3}$}% \message{//depth:\the\dp0//}% \box0%

A méréshez használt eszközök

  • volfrámszálas izzólámpa 12 V, 35W, (lámpaházban, kivezetésekkel), optikai padon csúsztatható
  • 4 színszűrő optikai padra erősítve
  • OHMEG ST-255 tápegység
  • 2 db HAMEG multiméter
  • GOM-802 milliohm-mérő
  • Fényintenzitás-mérő (Luxmérő)Voltcraft MS-1300
A mérési összeállítás.
A fénymérő
A fényforrás, a színszűrők és fénymérő (takarásban).

A színszűrők hullámhossz-adatai: Sárga: 570±60 nm Narancs: 650±90 nm Zöld: 540±40 nm Kék: 470±60 nm

Mérési feladatok

  • 1. Mérje meg az izzó hidegellenállását! A lámpaház végénél a vezetékeken levő két banánhüvelyt kösse össze a GOM-802 milliohm-mérővel (négyhuzalos ellenállásmérés!), a leolvasott érték az izzó hideg ellenállása. Ügyeljen arra, hogy a csatlakozások biztos kontaktust adjanak. Ne felejtse el feljegyezni a laboratórium hőmérsékletét!
  • 2. A lámpát árammérő közbeiktatásával kösse rá a tápegységre, és a lámpaház mögötti két banánhüvelyen mérje az izzón eső feszültséget! Győződjön meg arról, hogy a tápegység kimeneti feszültsége 0V-ra van állítva, majd kapcsolja be a tápegységet! A tápegység feszültségének szabályozásával az izzón eső feszültséget állítsa 2 V-ra. Ezt az értéket jegyezze fel az izzón átfolyó árammal együtt! Tolja az izzót és a fénymérőt tartalmazó állványt egymás után az egyes színszűrőkhöz, és olvassa le mindegyiknél a fénymérő által jelzett értéket. A fénymérő lux-ban (fotometriai mértékegység)méri a fényintenzitást, de a számértékére nem lesz szükségünk, mivel csak a logaritmált függvény meredekségét vizsgáljuk.
  • 3. Végezze el a 2. feladatot az izzón eső feszültség 12 V-ig, voltonként való növelése mellett. Minden feszültség beállításnál olvassa le az izzón átfolyó áramot is, és ebből számolja az ellenállást Ohm törvényével! Így mind a négy színhez kap egy 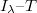\setbox0\hbox{$I_\lambda–T$}% \message{//depth:\the\dp0//}% \box0% adatsort.
  • Mit vár, a szűrőkön áthaladó sugárzások intenzitásai hogyan aránylanak egymáshoz? Az adatok elemzése alátámasztja-e ezt a várakozást. Ha nem, akkor mi lehet a magyarázata az eltérésnek?
  • 4. Ábrázolja mind a négy színszűrő esetében az 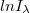\setbox0\hbox{$ln I_\lambda$}% \message{//depth:\the\dp0//}% \box0% adatokat 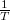\setbox0\hbox{$\frac{1}{T}$}% \message{//depth:\the\dp0//}% \box0% függvényében. Illesszen a pontokra egyenest, és a színszűrők hullámhossz-adatai alapján az egyenesek meredekségéből számítsa ki 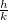\setbox0\hbox{$\frac{h}{k}$}% \message{//depth:\the\dp0//}% \box0% értékét mind a négy esetben. Számítsa ki ezek átlagát, és vesse össze eredményét a 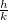\setbox0\hbox{$\frac{h}{k}$}% \message{//depth:\the\dp0//}% \box0% arány irodalmi értékével.

A mérés folyamán ügyeljen arra, hogy az izzóra ne jusson 12V-nál nagyobb feszültség! (A mérőszoba teljes besötétítésével biztosítsa, hogy a fénymérőbe csak az izzó fénye jusson!)

Irodalom

Budó Ágoston–Mátrai Tibor: Kísérleti fizika III. 304-307.§.

A hőmérsékleti sugárzás vizsgálata c. mérés leírása

PDF formátum

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Az_elektron_töltése_és_a_Boltzmann-állandó_hányadosának_(e/k)_mérése._A_Planck_és_a_Boltzmann-állandó_hányadosának_(h/k)_mérése.&oldid=14488”