„Függvényillesztés Monte Carlo módszerrel mérésleírás” változatai közötti eltérés
a |
|||
| 9. sor: | 9. sor: | ||
\label{MCEnergyEq} | \label{MCEnergyEq} | ||
$$ | $$ | ||
| − | A minimalizálást Monte Carlo--Metropolis algoritmussal végezzük: Változtassuk meg a paramétereket véletlenszerűen: $\vec{A}' = \vec{A}+ \vec{\delta A}$. Ezzel a | + | A minimalizálást Monte Carlo--Metropolis algoritmussal végezzük: Változtassuk meg a paramétereket véletlenszerűen: $\vec{A}' = \vec{A}+ \vec{\delta A}$. Ezzel a fentiek szerint kiszámolt energia is változik: $E(\vec{A}) \rightarrow E(\vec{A}')$. Az új paramétereket elfogadjuk, ha közelebb kerültünk a minimumhoz, tehát $E(\vec{A}') < E(\vec{A})$. Célunk elkerülni, hogy az algoritmus befagyjon egy lokális minimumba, ezért $p=\textrm{exp}(-\beta(E(\vec{A}')-E(\vec{A})))$ valószínűséggel dolgozunk tovább az új paraméterekkel, ha $E(\vec{A}') > E(\vec{A})$. Vegyük észre, hogy $\beta \rightarrow \infty$ esetben csak lefelé léphetünk, míg a $\beta \rightarrow 0$ határátmenetben véletlenszerű mozgást kapunk a paramétertérben. Ez adja a fizikai jelentését az algoritmusban szereplő $\beta$ értéknek: megfeleltethető egy, a paramétertérben mozgó részecske $(kT)^{-1}$ inverz hőmérsékletének. |
== Implementáció == | == Implementáció == | ||
A lap 2011. március 22., 14:32-kori változata
Tartalomjegyzék |
Bevezetés
A Monte Carlo algoritmusok szerteágazó alkalmazási területei közül a függvényillesztés a számítógépes gyakorlat témája. A leírás áttekinti a szükséges elméleti hátteret, valamint segítséget ad a konkrét megvalósításhoz.
Elméleti háttér
Legyen az illesztendő adatsor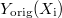
, ahol 
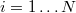. Az illesztett adatsor hasonlóan 
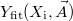, ahol 
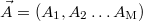a paraméterek listája, amelyek hangolásával érjük el, hogy az illesztett adatsor rásimuljon az eredetire. Ez a következő energiakifejezés minimalizálását jelenti: ![\[E(\vec{A})=\sum_{i=1}^{N} \left| Y_\textrm{orig}(X_\textrm{i}) - Y_\textrm{fit}(X_\textrm{i}, \vec{A})\right| \label{MCEnergyEq} \]](/images/math/b/c/9/bc95522349a8e6ac1157fbcc34e08ad7.png)
A minimalizálást Monte Carlo--Metropolis algoritmussal végezzük: Változtassuk meg a paramétereket véletlenszerűen: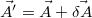 
. Ezzel a fentiek szerint kiszámolt energia is változik: 
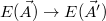. Az új paramétereket elfogadjuk, ha közelebb kerültünk a minimumhoz, tehát 
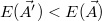. Célunk elkerülni, hogy az algoritmus befagyjon egy lokális minimumba, ezért 
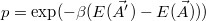valószínűséggel dolgozunk tovább az új paraméterekkel, ha 
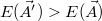. Vegyük észre, hogy 
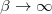esetben csak lefelé léphetünk, míg a 
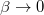határátmenetben véletlenszerű mozgást kapunk a paramétertérben. Ez adja a fizikai jelentését az algoritmusban szereplő 
értéknek: megfeleltethető egy, a paramétertérben mozgó részecske 
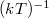inverz hőmérsékletének.
Implementáció
A fentiek megvalósításához a következő felépítést érdemes követni:
- Készítsünk globális tömböt az eredeti, valamint az illesztett adatsornak;
- Hasonlóan globális változókban tároljuk az inverz hőmérsékletet, az illesztési paramétereket, valamint azok lépésközét;
- Deklaráljunk két véletlenszám-generátort: egyet a paraméterek megváltoztatásához és egyet az
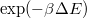valószínűségű lépéshez;
- Hozzunk létre globális változókat a megváltoztatott paramétereknek, valamint egy tömböt a megváltoztatott paraméterekkel generált illesztőfüggvénynek.
Az illesztés inicializálásához hozzuk létre a szükséges változókat, és olvassuk be a kezdőértékeket a TextBoxokból.
Az illesztést az alábbiak szerint végezzük:
- Számítsuk ki a
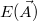szerinti energiát az aktuális változókkal;
- Változtassuk meg az egyik paramétert a megadott határok között egyenletes eloszlással;
- Számítsuk ki az így megváltozott energiát;
- A régi és új energia különbsége alapján döntsünk arról, hogy elfogadjuk-e a változást: ha az új érték kisebb, akkor minden esetben, ha nem, akkor sorsoljunk egy véletlenszámot, és 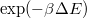valószínűséggel;
- Ha szükséges, írjuk ki az új értéket a TextBoxba, és ábrázoljuk a megváltozott illesztőfüggvényt;
- A fentiek szerint járjunk el a többi paraméter esetében.
Feladatok
Készítsünk grafikus függvényillesztő felületet a data.dat fileban található 500 elemű adatsor illesztéséhez a![\[ y(t)=Ae^{-t/\tau}\sin(2\pi t/T)\]](/images/math/4/f/0/4f0332aa1420c838cd15b43a82ebe856.png)
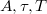a keresett paraméterek. A cél eléréséhez az alábbiak szerint haladjunk:
- Olvassuk be és ábrázoljuk a data.dat állomány tartalmát!
- Hozzunk létre TextBoxokat, amelyekkel állíthatóak a függvényillesztés kiinduló paraméterei, azok lépésköze, valamint az inverz hőmérséklet!
- Hozzunk létre gombokat, amelyekkel elindíthatjuk a függvényillesztést: legyen lehetséges újraindítani az illesztést a TextBoxokban megadott kezdeti paraméterekkel, valamint 1, illetve 100 illesztési ciklust elindítani!
- A program jelenítse meg az aktuális paramétereket, az 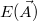szerinti energiát, valamint az illesztett függvényt!
A jegyzőkönyvben szerepeljen a program felépítésének leírása, valamint a probléma diszkussziója. Vizsgáljuk meg a kezdeti paraméterek, az inverz hőmérséklet, valamint a paraméterek lépésközeinek hatását az illesztés gyorsaságára és jóságára, azaz adjuk meg, hogy átlagosan hány lépés után illeszkedik a generált függvény az eredetire, valamint mekkora a jellemző minimális energia!
Opcionálisan próbáljuk ki, hogy lehetséges-e jobb eredményt elérni, ha -t, illetve a lépésközöket dinamikusan változtatjuk! A dokumentációhoz csatoljuk a program forráskódját!
