Időben változó elektromos és mágneses terek kapcsolata
Tartalomjegyzék |
A mágneses indukció és alkalmazásai
A Faraday törvény
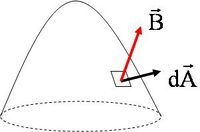
Idáig arra láttunk néhány példát, hogy az elektromos áram illetve az áramot létrehozó elektromos tér ( emlékszünk rá: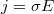 
) hogyan kelt indukciós teret maga körül. Kérdés, hogy a mágneses indukciós tér létre tud-e hozni elektromos teret. A válasz az, hogy igen, és ez a fejezet azt tárgyalja, hogy ez hogyan lehetséges. A jelenség vizsgálatához először definiáljuk mi is az indukciós tér fluxusa, amelyet, bár nem neveztük nevén, a mágneses Gauss törvényben már alkalmaztuk. Az elektrosztatikában már használtuk az elektromos tér fluxusának fogalmát. Az analógia most is működik; tehát (az 1.1.1 b ábra alapján) mágneses fluxus:
![\[\Phi _m = \int\limits_{A} \vec B d \vec A \]](/images/math/6/b/2/6b2b8ed5548f099a402659bb8bf19e6e.png) |
(1.1.1) |
Azaz az indukciós tér és az infinitezimális felületelemhez tartozó vektor skalárszorzatát kell a felületre kiintegrálni, hogy megkapjuk az indukciós tér fluxusát.
Több kísérlet is azt mutatja (pl. Mágneses indukció I. és Mágneses indukció III.), hogy az időben változó mágneses fluxus elektromos feszültséget indukál. Ennek matematikai megfogalmazása a Faraday törvény:
![\[\varepsilon = -\frac {d\Phi _m}{dt} \]](/images/math/4/3/0/4303fc70afe942e77e7cd8132edf91d6.png) |
(1.1.2) |
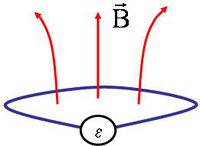
ahol 
az említett elektromos feszültség, más néven az elektromotoros erő. A negatív előjel szerepére még visszatérünk. Lássuk, hogyan is kell értelmezni a 1.1.2 törvényt! Ehhez tekintsük a 1.1.1 a és b ábrákat!
 |
 |
| 1.1.1 a ábra | 1.1.1 b ábra |
A 1.1.1 a sematikus ábra azt reprezentálja, hogy a kék vonallal jelölt zárt hurokban feszültség keletkezik. (Ha ezt a zárt hurkot egy létező vezetékdarab helyettesítené, akkor abban valóban áram folyna a változó fluxus hatására indukálódott elektromotoros erő miatt.) Rögtön felvetődhet a kérdés, hogy a zárt hurok által kifeszített lehetséges felületek közül - amelyeket éppen maga a zárt hurok határol - melyikre is kell a fluxust számítani (a 1.1.1 b ábra mutat egy ilyen határoló felületet). A válasz az, hogy bármelyik, a 1.1.1 b ábrán látható felülethez hasonló alakzat használható, mert a fluxus ugyanakkorának adódik mindegyikre. Amennyiben ez nem így lenne, akkor a két különböző fluxus-értéket adó felület által kialakított zárt térrész (és az azt határoló zárt felület) esetében a mágneses Gauss-törvény nem működne, ami azt jelentené, hogy mágneses monopólus van benne; ez pedig nem lehet. (Természetesen precízebb matematikai bizonyítás is létezik.)
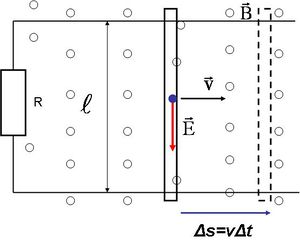
Ezután tekintsünk a 1.1.2 .a ábrán látható egyszerű gyakorlati példát!
 |
 |
| 1.1.2 a ábra | 1.1.2 b ábra |
A két párhuzamos, az 
ellenálláshoz kapcsolódó, hosszú, egymástól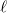 
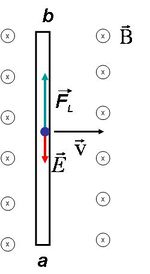
távolságra lévő (nem szigetelt) vezeték-páron mozog 
sebességgel egy fémrúd, melynek ellenállása elhanyagolható. Az indukciós tér – melyet a kis körök reprezentálnak – az ábra síkjából kifelé mutat. (Amennyiben a kis körökben kereszt is lenne, akkor befelé mutatna.) A fémrúddal zárttá tett áramkörben elektromotoros erő jön létre, mivel a rúd mozog és emiatt a fluxus változik; az ábra jelöléseit használva:
![\[\Delta \Phi _m = B\ell v \Delta t \]](/images/math/e/0/b/e0b6da3670e99f64e6bc1f0b53a10c02.png) |
(1.1.3) |
A Faraday-törvény alkalmazásával a zárt körben létrejövő feszültség nagysága:
![\[ \left| \varepsilon \right| = \frac {B\ell v \Delta t}{\Delta t} = B\ell v \]](/images/math/9/1/c/91cde41f7aac52e4d2fd77342abb13a1.png) |
(1.1.4) |
A zárt körben létrejövő, az ellenálláson is átfolyó áram:
![\[ I = \frac {B\ell v }{R} \]](/images/math/9/9/2/99200cfc55c8a1aa5bc7b45fca8c6458.png) |
(1.1.5) |
Az áram irányát a rúdban lévő töltésen kialakuló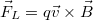 
erő és a belőle származtatható elektromos téresősség 
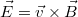alkalmazásával kapjuk (az indukált térerősség adja az áramirányt).
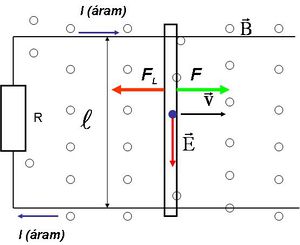
Az áramjárta vezetőre, vagyis a rúdra ható Lorentz-erő (1.1.2 b ábra):
![\[ F_L = BI\ell = \frac {B^2 \ell ^2 v }{R} \]](/images/math/f/1/d/f1d2ed750057efd057012427f6a1b1d3.png) |
(1.1.6) |
A rudat egyenletes sebességgel mozgató 
erő nagysága éppen az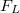 
– el megegyező, és teljesítménye:
![\[ P = F_L v = \frac {B^2 \ell ^2 v^2 }{R} \]](/images/math/f/d/3/fd3282ee868a466d7d512d709957fd5a.png) |
(1.1.7) |
Ez természetesen megegyezik az ellenálláson disszipált teljesítménnyel:
![\[ P = R I^2 = R \left(\frac{B\ell v}{R}\right)^2 = \frac {B^2 \ell ^2 v^2 }{R} \]](/images/math/5/b/c/5bc5e9fea5a5324b920d195a45fa6566.png) |
(1.1.8) |
Az áram irányát könnyen meghatároztuk ennél az egyszerű elrendezésnél a Lorentz-erő segítségével. Vegyük észre, hogy az említett modell esetében az indukcióval létrejött áram mágneses indukciós tere (Biot-Savart törvény) éppen ellenkező irányú az eredeti B – vel, azaz a rúd mozgatása miatt bekövetkező fluxusnövekedést igyekszik a rendszer "csökkenteni". Ez tehát általában azt jelenti, hogy a rendszer igyekszik kitérni a hatás alól, vagyis negatív visszacsatolás történik; ez az oka annak, hogy a 1.1.2 jobb oldalán megjelenik a negatív előjel. Vegyük észre, hogy ez éppen a Lenz-törvény, azaz: egy zárt körben indukált feszültség iránya olyan, hogy az általa keltett áram mágneses tere a fluxusváltozás, tehát az indukció ellen hat. Ez a törvény természetesen alkalmazható az említett áramkörnél jóval bonyolultabb elrendezések esetében is, és egyszerű magyarázatot ad különböző látványos kísérlet jelenségeire. Néha nem is szükséges, hogy egy zárt hurokban változzon a fluxus. Az indukció jelenségének kialakulásához elegendő ha egy viszonylag nagyméretű vezető darab mozog indukciós térben, esetleg bizonyos részein változik a mágneses fluxus. Ekkor örvényáramok jelennek meg az anyagon belül, melyek szintén – a Lenz-törvénynek megfelelően – negatív visszacsatolást jelentenek. A témához kapcsolódó videó: Mágneses indukció X.. Az örvényáramok megjelenése a Joule hő miatt melegítésre is használható. Az örvényáramok alkalmazására számos példa van villanyóra, indukciós forrasztás, stb…; a legismertebb közülük talán mégis az indukciós sütő vagy főzőlap .
 |
| 1.1.3 ábra |
A képen jól látható, hogy miért is előnyös indukciós főzőlapot használni. A fém serpenyőt – és benne az ételt – melegíti csak fel az indukcióval létrehozott örvényáram, a főzőlapot magát nem, így a sütés, főzés folyamata is energiatakarékosabb. Az örvényáramok miatti energia-disszipáció gyakran a vezetőből készült test mozgásának fékeződésében jelentkezik. [videó] Az indukció jelenségén alapul az energiatakarékos autókba beépített indukciós fék is, amely fékezésnél a mozgási energia egy részét ”visszatáplálja” az elektromotoros erő segítségével az akkumulátorba, így azt a későbbiekben gyorsításra, stb. lehet használni; egy ilyen autó városi fogyasztása akár 30 - 40%-al is kisebb lehet, mint egy hagyományos autóé (a gyártók szerint).
A mozgási indukció
Amennyiben egy fémvezető mozog indukciós térben, akkor kialakul az ún. mozgási indukció. A jelenség magyarázatához tekintsük az 1.2.1 ábrát!
 |
| 1.2.1 ábra |
Egy pozitív – a rúddal együtt mozgó – 
töltésre a 
térben hat a Lorentz-erő. Emiatt töltések mozdulnak el a rúd végei felé és ott fel is halmozódnak mindaddig, amíg az általuk keltett elektromos tér hatása ki nem ejti a Lorentz-erőt (hasonló magyarázatot már láttunk a Hall-effektusról szóló fejezetben), azaz:
![\[ qE = qvB \qquad \Longrightarrow \qquad E = vB \]](/images/math/8/8/a/88a466ba48e2658367cd12d871277d63.png) |
(1.2.1) |
Ebből megkaphatjuk a fémrúd 
és 
vége közötti indukált feszültséget, azaz az elektromotoros erőt:
![\[ \varepsilon = V_{ab} = E\ell = vB\ell \]](/images/math/c/2/2/c229a47cf16e2e6b41658de35baed175.png) |
(1.2.2) |
A dinamó működése is a mozgási indukción alapul.
A generátor
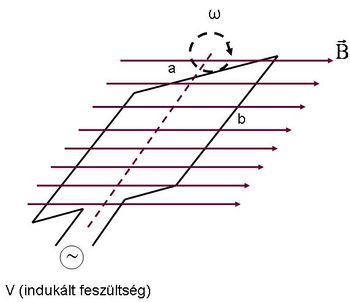
Az indukció jelenségén alapuló berendezések közül valószínűleg a legfontosabb a váltakozó feszültséget (ill. áramot) keltő generátor, amelynek igen leegyszerűsített vázlata látható az 1.3.1 ábrán:
 |
| 1.3.1 ábra |
Az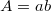 
területű vezető keret 
szögsebességgel egyenletesen forog. A mágneses fluxus felírható a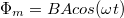 
formában. Faraday-törvényének 1.1.2 felhasználásával kapjuk az indukált feszültséget, más néven a váltakozó feszültséget:
![\[ \varepsilon = -\frac {d\Phi _m}{dt}= V(t) = BA\omega sin(\omega t) = V_0 sin(\omega t) \]](/images/math/d/2/4/d249a1462c6ab5bcff99dd3cda8261e4.png) |
(1.3.1) |
A generátor segítségével tehát mechanikai teljesítményt tudunk átalakítani elektromos teljesítménnyé. Az atomerőművek, a szénerőművek, vagy a gáz erőművek a termelt hőmennyiséget alakítják át elektromos energiává. A következő képen egy erőmű generátorai láthatók:
 |
| 1.3.2 ábra |
A szél és a vízi erőművekben szintén generátort alkalmaznak.
Az önindukció
Idáig olyan példákat vizsgáltunk, amelyeknél a külső mágneses tér fluxus-változása indukálta az elrendezésben kialakuló elektromotoros erőt. Most nézzük meg, hogy mi történik akkor, ha egy A keresztmetszetű, 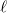hosszúságú, 
menetű szolenoidon átfolyó áram erőssége (esetleg iránya is) időfüggő: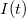 
. Megmutattuk, hogy a szolenoidban kialakuló csaknem homogén mágneses tér nagyságát hogyan lehet kiszámítani a (Mozgó töltések és áramok által keltett tér 1.2.4) segítségével. Az indukciós tér fluxusa az említett formula alkalmazásával:
![\[ \Phi_m = BA = \frac {\mu NIA}{\ell} \]](/images/math/a/0/e/a0e7b3cf595a9709d3d3e939e9516567.png) |
(1.4.1) |
Itt kihasználtuk azt a tényt, hogy a szolenoidon kívül az indukciós tér erőssége csaknem zérus.
A tekercsben indukált feszültséget most már könnyű kiszámítani a Faraday-törvénnyel:
![\[ \varepsilon = -N\frac {d\phi_m}{dt} = V_ind. (t)= -\frac {\mu N^2IA}{\ell} \frac {dI}{dt} \]](/images/math/4/c/4/4c43589b285d565e99581f84f4b61e59.png) |
(1.4.2) |
A mágneses fluxus idő szerinti deriváltját azért kellett – el beszorozni, mert az indukciós tér fluxusának deriváltjaként megjelenő elektromotoros erő a szolenoid minden egyes menetén indukálódik, és a tekercs menetei sorba vannak kötve. Az eredményt megfogalmazhatjuk általánosabb formában is:
![\[ \varepsilon = -L\frac {dI}{dt} \]](/images/math/8/5/a/85ab84f600c54fe6ac0a736b8d5ab78b.png) |
(1.4.3) |
