Megmaradási törvények a mechanikában
A Fizikában felfedezhetünk olyan átfogó törvényeket, amelyek gondolataink startkövei lehetnek, és iránymutatóként működhetnek. Az ún. „megmaradási tételek” (is) ilyenek. Bármilyen összetett is legyen egy (mechanikai) rendszer, és bármilyen bonyolult módon is mozogjék, ha az előírt feltételek teljesülnek, bizonyos tulajdonságai állandóak maradnak. Ez lehetővé teszi azt, hogy az igen bonyolult mozgásegyenletek megoldása nélkül is egzakt eredményekre jussunk. Ezen törvények megfelelő általánosításával a ma ismert Univerzum egészére érvényes állításokat tehetünk.
A megmaradási tételek számos természeti jelenségben felismerhetők, és segítségükkel technikai alkalmazások és a sportokban alkalmazott „trükkök” is könnyebben megérthetők.
Tartalomjegyzék[elrejtés] |
Munka, teljesítmény, energia
A munka és a teljesítmény fogalma
A fizikában sok olyan fogalmat használunk, ami a hétköznapi életből származik, azonban a jelentése nem ugyanaz a fizikában, mint a hétköznapi nyelvhasználatban. Ilyen fogalom a munka és a teljesítmény is.
A mechanikai munka két test közötti energiaátadás egyik lehetséges módja. Az elemi munkát a![\[\Delta W=\vec{F}\Delta\vec{s}\]](/images/math/7/e/0/7e03bec6a4be86286a073b153d81cfc4.png)
![\[W=\int_g\vec{F}{\rm d}\vec{s}\]](/images/math/f/3/9/f39722dacfe0843e496f60f9c76bef54.png)
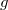 arra utal, hogy egy görbe, a test pályája mentén kell integrálni. Ha
arra utal, hogy egy görbe, a test pályája mentén kell integrálni. Ha 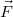 állandó, akkor az integrál helyett a munka egy egyszerű skalárszorzattal kiszámítható:
állandó, akkor az integrál helyett a munka egy egyszerű skalárszorzattal kiszámítható: ![\[W=\vec{F}\vec{s}=Fs\cos\alpha\]](/images/math/f/8/2/f825b67d72af3d502e85cdd6f45d7edc.png)
 az erő- és az elmozdulásvektor által bezárt szög.
A teljesítmény a munkavégzés sebességét fejezi ki:
az erő- és az elmozdulásvektor által bezárt szög.
A teljesítmény a munkavégzés sebességét fejezi ki: ![\[P=\frac{{\rm d}W}{{\rm d}t}=\frac{\vec{F}{\rm d}\vec{s}}{{\rm d}t}=\vec{F}\vec{v}\]](/images/math/6/7/6/676894b9e2d7904e7eb46b51b1fcff45.png)
A munka SI mértékegysége a joule, 1 J = 1 Nm, a teljesítményé a watt, 1 W = 1 J/s.
Mozgási energia
Vizsgáljunk egy testet, mely a rá ható erők hatására valamilyen pályán mozog. Az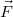 eredő erő munkája
eredő erő munkája ![\[W=\int_1^2\vec{F}{\rm d}\vec{s}\]](/images/math/f/b/9/fb9302f2a4cc48f511fa92e15510c9f9.png)
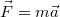 , valamint a gyorsulás és a sebesség definícióját, a kifejezés átalakítható:
, valamint a gyorsulás és a sebesség definícióját, a kifejezés átalakítható: ![\[W=\int_1^2 m\vec{a}{\rm d}\vec{s}=m\int_1^2\frac{{\rm d}\vec{v}}{{\rm d}t}{\rm d}\vec{s}=m\int_1^2{\rm d}\vec{v}\frac{{\rm d}\vec{s}}{{\rm d}t}=m\int_{v_1}^{v_2}\vec{v}{\rm d}\vec{v}\]](/images/math/d/c/9/dc9fb2828305ccddef0b96e21b616e67.png)
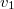 és
és 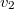 a testsebessége a vizsgált mozgás elején és végén. Az integrálást elvégezve:
a testsebessége a vizsgált mozgás elején és végén. Az integrálást elvégezve: ![\[W=m\int_{v_1}^{v_2}\vec{v}{\rm d}\vec{v}=m\left[\frac{1}{2}v^2\right]_{v_1}^{v_2}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\]](/images/math/9/a/2/9a2130e000126d1e2029af00d5434c4f.png)
![\[E_m=\frac{1}{2}mv^2\]](/images/math/5/f/f/5ffb4aac659dbfc06bca9bfeeb9fadd0.png)
![\[W=\Delta E_m\]](/images/math/8/5/8/8580ecf0990386c73ab3921be889ac83.png)
Helyzeti energia
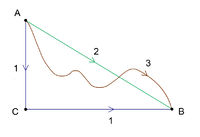
Bizonyos erőhatások esetében az erő által végzett munka nem függ a pálya alakjától, csak a kezdő és végpontoktól. Például az 1. ábrán az A pontból a B pontba három különböző útvonalon kiszámolva a munkát, azt kapjuk, hogy az mindhárom útvonalon egyforma:![\[W_1=W_{AC}+W_{CB}=mgh+0=mgh\]](/images/math/e/2/6/e2658b41d6c79e69d5cff8f691d60356.png)
![\[W_2=m\vec{g}\vec{s}=mgs\cos\alpha=mgh\]](/images/math/d/5/c/d5c5f6bd2ebb810a81a4867a1080e8d3.png)
![\[W_3=\int_A^B m\vec{g}{\rm d}\vec{s}=m\vec{g}\int_A^B {\rm d}\vec{s}=m\vec{g}\vec{s}=mgh\]](/images/math/e/8/4/e84607ee458c888f9d989b25f1351e98.png)
![\[\oint\vec{F}{\rm d}\vec{s}=\int_{A(1)}^B \vec{F}{\rm d}\vec{s}+\int_{B(2)}^A \vec{F}{\rm d}\vec{s}=\int_{A(1)}^B \vec{F}{\rm d}\vec{s}-\int_{A(2)}^B \vec{F}{\rm d}\vec{s}=W_{AB(1)}-W_{AB(2)}=0\]](/images/math/9/5/f/95f4a4f3880bc77b2dbd667915295f86.png)
![\[E_{hA}=\int_A^O\vec{F}{\rm d}\vec{s}=-\int_O^A\vec{F}{\rm d}\vec{s}=W_{AO}=-W_{OA}\]](/images/math/0/e/a/0ea90db891bbbb755cadbc24238e6bdd.png)
![\[W_{AB}=W_{AO}+W_{OB}=E_{hA}-E_{hB}=-\Delta E_h\]](/images/math/2/2/6/22654f1677a68c8230f3d9c2d6774529.png)
![\[W_k+W_{nk}=\Delta E_m\]](/images/math/4/b/4/4b421e3a008a7536580955dd38d0472d.png)
![\[W_k=-\Delta E_h\]](/images/math/1/2/b/12b25eb89996f87284357d7d39398424.png)
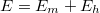 mechanikai energiát a következő összefüggést kapjuk:
mechanikai energiát a következő összefüggést kapjuk: ![\[W_{nk}=\Delta E_m+\Delta E_h=\Delta\left(E_m+E_h\right)=\Delta E\]](/images/math/7/1/0/7100616a0e3ace06574b63f77cf32e0f.png)
![\[W_{nk}=0\quad\Leftrightarrow\quad E={\rm const.}\]](/images/math/d/5/7/d57618c4c846a389e6a11fd5b106cb92.png)
Ez a mechanikai energia megmaradásának tétele egy tömegpontra.
Impulzus és perdület
Tömegpont impulzusa, Newton II. törvénye impulzussal megfogalmazva
A megmaradási tételek sok feladat megoldását megkönnyítik. A mechanikai energia után ezért bevezetjük az impulzus (vagy másképp lendület) fogalmát. Az impulzus vektoriális mennyiség, egy tömegpont impulzusa a tömeg és a sebességvektor szorzata:![\[\vec{p}=m\vec{v}\]](/images/math/1/b/8/1b8235c049c408e5ddf30af8e589d191.png)
![\[\frac{{\rm d}\vec{p}}{{\rm d}t}=\frac{{\rm d}(m\vec{v})}{{\rm d}t}=m\frac{{\rm d}\vec{v}}{{\rm d}t}=m\vec{a}=\vec{F}\]](/images/math/e/3/c/e3c3dfcba3ce4df9c43d2247b46aa783.png)
![\[\vec{F}=0\quad\Leftrightarrow\quad\vec{p}={\rm const.}\]](/images/math/8/c/a/8ca1953adf8b3ac6506fdef8bff795db.png)
Ez az impulzus megmaradásának tétele egy tömegpontra.
Tömegpont perdülete, perdület és forgatónyomaték kapcsolata
Ugyanilyen megfontolásból bevezetjük a perdület (vagy másképpen impulzusmomentum) fogalmát is. A perdület szintén vektoriális mennyiség, az O pontra vonatkoztatott perdületet a következő vektoriális szorzattal definiálunk:![\[\vec{N}=\vec{r}\times\vec{p}=m\vec{r}\times\vec{v}\]](/images/math/0/8/e/08eee0b3ad8f957a6529cbb84c762c55.png)
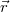 az O pontból a tömegpontba mutató helyvektor.
Deriváljuk ezt a kifejezést is idő szerint:
az O pontból a tömegpontba mutató helyvektor.
Deriváljuk ezt a kifejezést is idő szerint: ![\[\frac{{\rm d}\vec{N}}{{\rm d}t}=\frac{{\rm d}(\vec{r}\times\vec{p})}{{\rm d}t}=\frac{{\rm d}\vec{r}}{{\rm d}t}\times\vec{p}+\vec{r}\times\frac{{\rm d}\vec{p}}{{\rm d}t}=\vec{v}\times\vec{p}+\vec{r}\times\vec{F}\]](/images/math/c/6/9/c69470a60168b718c36c5b75bdde2981.png)
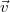 és
és 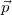 párhuzamos, a második tag pedig az
párhuzamos, a második tag pedig az 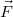 eredő erő forgatónyomatéka:
eredő erő forgatónyomatéka: ![\[\vec{M}=\vec{r}\times\vec{F}\]](/images/math/7/e/0/7e05bf4950c432027287dfce89ca0bf4.png)
![\[\frac{{\rm d}\vec{N}}{{\rm d}t}=\vec{M}\]](/images/math/5/1/c/51c85fb9a2790e9dabb55cd548f950de.png)
![\[\vec{M}=0\quad\Leftrightarrow\quad\vec{N}={\rm const.}\]](/images/math/e/2/7/e271df62524e4e5fbec32ff7aca898d7.png)
Ez a perdület megmaradásának tétele egy tömegpontra.
Megmaradási tételek
Pontrendszer fogalma
A pontrendszer tömegpontokból áll. Szabadon megválasztható, hogy mely pontok tartoznak a rendszerhez. A modell használható néhány testből álló rendszerek (például ütközések, Föld-Hold rendszer), nagyon sok tömegpontból álló rendszerek (például gázok, 10 részecske) és a kiterjedt testek (például merev testek) leírására.
részecske) és a kiterjedt testek (például merev testek) leírására.
![\[m=\sum_i m_i\]](/images/math/7/9/1/7919962b3d5cef651743ed7551a0004f.png)
![\[\vec{r}_{{\rm TKP}}=\frac{1}{m}\sum_i m_i\vec{r}_i\]](/images/math/f/3/b/f3b1458cfd8912a61cdd325e0714c99e.png)
Impulzusmegmaradás tétele
A pontrendszer impulzusa a tömegpontok impulzusának összege. A kifejezést átalakítva és felhasználva a tömegközéppont definícióját:![\[\vec{p}=\sum_i\vec{p}_i=\sum_i m_i\vec{v}_i=\sum_i m_i\frac{{\rm d}\vec{r}_i}{{\rm d}t}=\frac{{\rm d}\left(\sum_i m_i\vec{r}_i\right)}{{\rm d}t}=\frac{{\rm d}\left(m\vec{r}_{{\rm TKP}}\right)}{{\rm d}t}=m\frac{{\rm d}\vec{r}_{{\rm TKP}}}{{\rm d}t}=m\vec{v}_{{\rm TKP}}\]](/images/math/d/4/c/d4cd827dd9c6bcda2a88a6fe023dcc38.png)
A pontrendszer impulzusa tehát úgy számolható, mintha az egész tömeg egyetlen pontként a tömegközéppont sebességével mozogna.
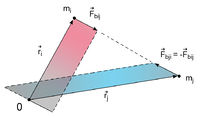
A pontrendszer minden pontjára hathatnak erők. Az erők egy része a pontrendszeren kívüli testekkel való kölcsönhatás eredménye, ezeket nevezzük külső erőknek. Az 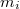 tömegpontra ható külső erők eredője
tömegpontra ható külső erők eredője 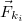 Ezen kívül a pontrendszer tagjai között is felléphetnek erőhatások, ezeket belső erőknek nevezzük. Az
Ezen kívül a pontrendszer tagjai között is felléphetnek erőhatások, ezeket belső erőknek nevezzük. Az 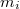 tömegpontra az
tömegpontra az 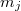 tömegpont
tömegpont 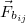 erővel hat.
erővel hat.
![\[\frac{{\rm d}\vec{p}_i}{{\rm d}t}=\vec{F}_{k_i}+\sum_{j\neq i}\vec{F}_{b_{ij}}\]](/images/math/7/7/6/776e8a227eb43e48ea9e005806166153.png)
![\[\sum_i\frac{{\rm d}\vec{p}_i}{{\rm d}t}=\sum_i\vec{F}_{k_i}+\sum_i\sum_{j\neq i}\vec{F}_{b_{ij}}\]](/images/math/9/f/d/9fdbb4096158778944ce2777f39f2ae3.png)
![\[\sum_i\frac{{\rm d}\vec{p}_i}{{\rm d}t}=\frac{{\rm d}\vec{p}}{{\rm d}t}\]](/images/math/a/0/8/a08b9399a10106d167882435770e251a.png)
![\[\sum_i\vec{F}_{k_i}=\vec{F}_k\]](/images/math/6/0/f/60fcd9b3068db71ec1fdb26361bc5251.png)
![\[\vec{F}_{b_{ij}}=-\vec{F}_{b_{ji}}\quad\Rightarrow\quad\sum_i\sum_{j\neq i}\vec{F}_{b_{ij}}=0\]](/images/math/a/8/7/a87000fa6d757e23bc8c8b2bce4b3263.png)
![\[\frac{{\rm d}\vec{p}}{{\rm d}t}=\vec{F}_k\]](/images/math/1/1/9/119459dce7eb6462e42e4896b6882f9c.png)
![\[\vec{F}_k=0\quad\Leftrightarrow\quad\vec{p}={\rm const.}\]](/images/math/d/5/e/d5e4f4176222b1d02eda0ecaec294d6d.png)
Ez az impulzus megmaradásának tétele pontrendszerre. Érdemes még egyszer hangsúlyozni, hogy a megmaradási tétel feltételében a belső erők nem szerepelnek, belső erők nem tudják megváltoztatni a rendszer impulzusát.
Perdületmegmaradás tétele
A pontrendszer tömegpontjaira ható erőknek – egy kiválasztott O pontra – forgatónyomatéka is lehet. Az erőkhöz hasonlóan a forgatónyomatékok is részben a pontrendszeren kívüli testekkel való kölcsönhatásból származnak, ezeket nevezzük külső forgatónyomatékoknak. Az 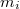 tömegpontra ható külső erők forgatónyomatékának eredője az O pontra
tömegpontra ható külső erők forgatónyomatékának eredője az O pontra 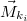 A pontrendszer tagjai között ható erők forgatónyomatékait belső forgatónyomatékoknak nevezzük. Az
A pontrendszer tagjai között ható erők forgatónyomatékait belső forgatónyomatékoknak nevezzük. Az 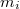 tömegpontra az
tömegpontra az 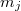 tömegpont az O pontra vonatkoztatva
tömegpont az O pontra vonatkoztatva 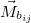 forgatónyomatékot fejt ki.
forgatónyomatékot fejt ki.
![\[\frac{{\rm d}\vec{N}_i}{{\rm d}t}=\vec{M}_{k_i}+\sum_{j\neq i}\vec{M}_{b_{ij}}\]](/images/math/f/6/a/f6adc0f1eb70489667626f9fa3ecfd11.png)
![\[\sum_i\frac{{\rm d}\vec{N}_i}{{\rm d}t}=\sum_i\vec{N}_{k_i}+\sum_i\sum_{j\neq i}\vec{N}_{b_{ij}}\]](/images/math/2/c/3/2c329c06a45c9ca9638ce290439e1bdb.png)
![\[\sum_i\frac{{\rm d}\vec{N}_i}{{\rm d}t}=\frac{{\rm d}\vec{N}}{{\rm d}t}\]](/images/math/0/0/d/00d76bba4e9dd6daa3e38ed1bde3d607.png)
![\[\sum_i\vec{M}_{k_i}=\vec{M}_k\]](/images/math/f/c/9/fc93c2691d60b6bca3dfad57965ea6f1.png)
![\[\vec{M}_{b_{ij}}=\vec{r}_i\times\vec{F}_{b_{ij}}=-\vec{r}_j\times\vec{F}_{b_{ji}}=-\vec{M}_{b_{ji}}\quad\Rightarrow\quad\sum_i\sum_{j\neq i}\vec{M}_{b_{ij}}=0\]](/images/math/f/9/6/f96f9039b6a73328e44a950b88fad59f.png)
![\[\frac{{\rm d}\vec{N}}{{\rm d}t}=\vec{M}_k\]](/images/math/a/c/0/ac04663bd45d503080e4b3fcb1cc605d.png)
![\[\vec{M}_k=0\quad\Leftrightarrow\quad\vec{N}={\rm const.}\]](/images/math/b/5/a/b5a465dbc88f98c6e53ba4c51e9849d3.png)
Ez a perdület megmaradásának tétele pontrendszerre. A megmaradási tétel feltételében a belső erők forgatónyomatéka sem szerepel, belső forgatónyomatékok nem tudják megváltoztatni a rendszer perdületét.
A perdületmegmaradás tételét bemutató kísérleti videók.
A mechanikai energia megmaradásának tétele
A rendszer pontjaira ható erők munkát is végeznek. A munkavégzéseket is csoportosíthatjuk aszerint, hogy külső vagy belső erők végzik. Ezen kívül érdemes megkülönböztetni a konzervatív és nemkonzervatív erők munkáját is. Írjuk fel a munkatételt minden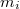 tömegpontra:
tömegpontra: ![\[W_{k,k_i}+W_{k,nk_i}+\sum_{j\neq i}W_{b,k_{ij}}+\sum_{j\neq i}W_{b,nk_{ij}}=\Delta E_{m_i}\]](/images/math/f/3/2/f32af77be87a301a555d5ecef48afce2.png)
![\[W_{k,k_i}=-\Delta E_{h_i}\]](/images/math/a/4/5/a45968db7059e729498ce5e817a9acac.png)
![\[W_{b,k_{ij}}=-\Delta E_{h_{ij}}\]](/images/math/6/1/5/6150d1295b7d20529f53024eda9dc8e3.png)
![\[W_{k,nk_i}+\sum_{j\neq i}W_{b,nk_{ij}}=\Delta E_{m_i}+\Delta E_{h_i}+\sum_{j\neq i}\Delta E_{h_{ij}}=\Delta E_i\]](/images/math/2/d/5/2d516a53857728e2d815011c30d69ac8.png)
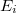 az
az 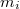 tömegpont teljes mechanikai energiája.
Összeadva az összes tömegpontra az egyenleteket
tömegpont teljes mechanikai energiája.
Összeadva az összes tömegpontra az egyenleteket ![\[\sum_i W_{k,nk_i}+\sum_i\sum_{j\neq i}W_{b,nk_{ij}}=\sum_i\Delta E_i\]](/images/math/e/8/4/e84aad3dcbbc6966eb280e42e9ff4cd5.png)
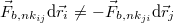 ). Tehát a rendszer teljes mechanikai energiáját a külső és a belső nemkonzervatív erők munkája tudja megváltoztatni:
). Tehát a rendszer teljes mechanikai energiáját a külső és a belső nemkonzervatív erők munkája tudja megváltoztatni: ![\[W_{k,nk}+W_{b,nk}=\Delta E\]](/images/math/d/f/5/df5ec04da0c31f977442b0c47c1adc7e.png)
![\[W_{k,nk}+W_{b,nk}=0\quad\Leftrightarrow\quad E={\rm const.}\]](/images/math/4/0/b/40b414b0519dce767955ef90ed4739f0.png)
Ez a mechanikai energia megmaradásának tétele pontrendszerre.
Bolygómozgás és műholdak
Kepler II. törvénye (perdületmegmaradás)
Kepler a XVII. század elején Tycho Brahe csillagászati megfigyelései alapján fogalmazta meg a bolygók mozgását leíró tapasztalati törvényeit:
I. A bolygók pályája ellipszis, melynek egyik gyújtópontjában van a Nap.
II. A Napból egy bolygóhoz húzott szakasz azonos idő alatt azonos területet súrol.
III. A bolygópályák fél nagytengelyeinek köbei úgy aránylanak egymáshoz (egy naprendszeren belül), mint a keringési idejük négyzetei.
A III. törvény fontos kísérleti előzménye volt Newton gravitációs törvényének. A II. törvény pedig szép példa a perdületmegmaradásra:
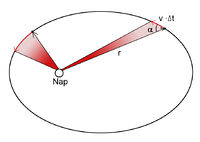
A bolygóhoz húzott szakasz által kicsiny idő alatt súrolt terület a 3. ábra alapján:
idő alatt súrolt terület a 3. ábra alapján: ![\[A=\frac{1}{2}r\left(v\Delta t\right)\sin\alpha=\frac{\Delta t}{2}rv\sin\alpha\]](/images/math/1/5/4/15419496e01de234c3bbad2ae92098c1.png)
![\[rv\sin\alpha=|\vec{r}\times\vec{v}|={\rm const.}\]](/images/math/f/9/4/f94a1c0934b432cebb29bf800ba175a1.png)
![\[\vec{N}=\vec{r}\times\vec{p}=m(\vec{r}\times\vec{v})\]](/images/math/1/4/4/1441d8a77ba7c361a832378a4dd7612c.png)
Kepler II. törvénye tehát – csillagászati megfigyelések tapasztalata alapján – a bolygó (Napra vonatkoztatott) perdületének állandóságát mondja ki.
A Nap körül keringő bolygóra a Nap gravitációs vonzása hat (a többi bolygó hatása emellett elhanyagolható). Ez az erő mindig egy pontba, a Nap felé mutat (ún. centrális erő), ezért forgatónyomatéka (a Napra, mint középpontra vonatkoztatva) mindig nulla. Ebből következik, hogy a bolygó perdületének valóban állandónak kell lennie:![\[\vec{M}=0\quad\Rightarrow\quad\vec{N}={\rm const.}\]](/images/math/7/3/e/73e9aa444ff7100d8dde90bc60ddcd37.png)
Rakétaelv (impulzusmegmaradás)
A világűrben, a Föld légkörén kívül az űrhajóra csak a környező égitestek gravitációs ereje hat. Pályáját a gravitációs erőtér és a kezdeti feltételek határozzák meg. Ha csak egyetlen égitest hat rá, akkor kör-, ellipszis-, parabola- vagy hiperbolapályán fog mozogni.
A pálya megváltoztatására (gyorsításra, lassításra, irányváltoztatásra) egyetlen lehetőség van: az űrhajó nagy sebességgel anyagot (forró égésterméket) lövell ki magából. Az űrhajó és a kilövellt gáz közti erőhatás belső erő, amely nem változtathatja meg az űrhajó - kilövellt gáz rendszer összimpulzusát. Ezért ha a gáz nagy sebességgel hátrafelé áramlik ki, akkor az űrhajó előrefelé fog gyorsulni. Ez a rakétaelv, amelynek részleteit Ciolkovszkij dolgozta ki a XIX. század legelején.
A sugárhajtású repülőgépekkel szemben az űrhajó csak olyan anyagot tud kilövellni, amelyet magával visz (szilárd vagy folyékony tüzelőanyag és oxigén vagy más oxidálószer), emiatt nagy végsebességhez nagy induló tömegre van szükség. A kiürült üzemanyagtartályokat nem célszerű tovább gyorsítani, ezért azok leválnak az űrhajóról (többlépcsős rakéták).
Kozmikus sebességek (energiamegmaradás)
A Föld körül körpályán keringő űrhajó sebessége Newton II. törvénye és gravitációs törvénye alapján könnyen meghatározható. A körpályához szükséges centripetális gyorsulást a gravitációs erő biztosítja:![\[m\frac{v^2}{r}=\gamma\frac{mm_F}{r^2}\]](/images/math/8/7/c/87ce397035f5e095ca7e7c7fd91a34b7.png)
 az űrhajó,
az űrhajó, 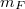 a Föld tömege,
a Föld tömege,  a pálya sugara,
a pálya sugara,  a gravitációs állandó. Felhasználva,hogy
a gravitációs állandó. Felhasználva,hogy 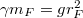 (
(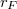 a Föld sugara)
a Föld sugara) ![\[v=\sqrt{\frac{\gamma m_F}{r}}=\sqrt{\frac{gr_F^2}{r}}\]](/images/math/6/2/8/628e1bf7dfbaf180ea7254bd2f4ddf6a.png)
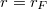 ) – ami persze a légellenállás miatt képtelenség, de néhány tíz km-es magasságban már lehetséges – akkor
) – ami persze a légellenállás miatt képtelenség, de néhány tíz km-es magasságban már lehetséges – akkor ![\[v_1=\sqrt{gr_F}\approx 7,9\,{\rm km/s}\]](/images/math/2/5/c/25c60b5b7a091d44e624c226665a1d11.png)
Ez az első kozmikus sebesség. Legalább ekkora sebességre kell gyorsítani egy űrhajót a Föld felszínén, hogy Föld-körüli pályára állhasson. (A Föld forgása miatt az egyenlítőn már a Földön álló úrhajónak is kb. 460 m/s sebessége van, ezért építik az űrközpontokat minél közelebb az egyenlítőhöz.)
A második kozmikus sebesség (vagy szökési sebesség az a sebesség, amivel az űrhajónak ahhoz kell rendelkeznie a Föld felszínén, hogy végleg elhagyja a Földet. Ennek meghatározásához használjuk fel, hogy a már kikapcsolt hajtóművű űrhajó teljes mechanikai energiája állandó:![\[E=E_m+E_h={\rm const.}\]](/images/math/9/1/7/917117b0be52d3c323b62a728833b0c5.png)
![\[E_h=-\int_{r_0}^r F{\rm d}r=-\int_{r_0}^r -\gamma\frac{mm_F}{r^2}{\rm d}r=-\gamma mm_F \left(\frac{1}{r}-\frac{1}{r_0}\right)\]](/images/math/c/3/e/c3ea903229ea26c008b5a6fa482b1223.png)
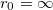 ), akkor
), akkor ![\[E_h=-\gamma\frac{mm_F}{r}=-m\frac{gr_F^2}{r}\]](/images/math/f/a/4/fa4dc32881a54a6cf09fb48805f941e1.png)
![\[E_m+E_h=\frac{1}{2}mv_2^2-m\frac{gr_F^2}{r_F}=0\]](/images/math/b/1/b/b1be6ed2364ee051eba9b312a8355793.png)
![\[v_2=\sqrt{2gr_F}=\sqrt{2}v_1\approx 11,2\,{\rm km/s}\]](/images/math/8/e/d/8ed25cb84a1188e6c9e347ed945cc385.png)
A távközlési és navigációs műholdak pontosan meghatározott pályákon keringenek a Föld körül. A műholdakat nagy hordozórakéták emelik Föld-körüli pályára (minél magasabb a pálya, annál több energiára van szükség a pályára állításhoz).
A távközlési műholdak a forgó Földhöz képest állnak, hogy a Földről rögzített parabolaantennával lehessen velük kapcsolatot tartani. Ehhez a műholdnak pontosan egy nap (egy csillag-nap) alatt kell megkerülniük a Földet az egyenlítő síkjában. Felírva a mozgásegyenletet![\[m\omega^2r=\gamma\frac{mm_F}{r^2}=m\frac{gr_F^2}{r^2}\]](/images/math/c/a/4/ca4096d5f11d670e658658c5b55e5f80.png)
![\[r^3=\frac{gr_F^2}{\omega^2}=\frac{gr_F^2T^2}{4\pi^2}\]](/images/math/b/0/3/b0329be9376b56d1c195ba62f9da8bca.png)
![\[r\approx 40200\,{\rm km}\qquad h=r-r_F\approx 35800\,{\rm km}\]](/images/math/d/d/8/dd8a48601b7ff0fa9667de226eaad11e.png)
A GPS rendszer műholdjai ennél valamivel alacsonyabban (kb. 20 ezer km), sok más műhold (pl. fényképező, időjárási műholdak) pedig sokkal alacsonyabb pályán keringenek. (A Nemzetközi űrállomás például mindössze 360 km magasan.) A műholdak a különböző zavarok (az alacsony pályákon elsősorban a magas légkör fékező hatása) miatt pályakorrekciókra szorulnak. Erre a célra a műholdakon kisteljesítményű rakéták vannak. Az alacsony pályán keringő, és így a légkör miatt erősebb fékezésnek kitett műholdakat időnként újra magasabb pályára kell állítani. Ehhez a műholdat a keringés irányában a rakéták segítségével gyorsítani kell. (Ha elfogy a manőverekre szánt üzemanyag, akkor a műhold egyre mélyebbre süllyed, és végül elég a sűrűbb légkörben.)
Merev test forgása
Tehetetlenségi nyomaték
A merev test a valóságos testek egy modellje: a tömegponttal szemben figyelembe veszi a test alakját, forgását is, de a valóságos testek (rugalmas vagy képlékeny) alakváltozásait nem. A merev test leírásához felhasználható, amit a pontrendszerekről megállapítottunk, hiszen a merev test egy speciális pontrendszerként kezelhető (ahol a pontok egymáshoz képest nem mozoghatnak).
A merev test mozgása felépíthető elemi elmozdulásokból és elfordulásokból. A merev test haladó mozgása ugyanúgy leírható, mint a tömegponté: a testet ekkor a tömegközéppontjába koncentrált tömegpontként kezelhetjük. A forgás általános esetben nagyon bonyolult lehet, itt két esettel, a rögzített tengely körüli forgással és a pörgettyűmozgással foglalkozunk.
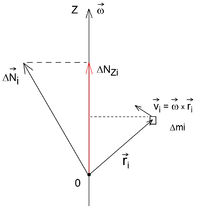
Egy rögzített tengely körül forgó merev test tengelye (és így szögsebességvektora) legyen -irányú. A merev test egy elemi tömegdarabjának perdülete
-irányú. A merev test egy elemi tömegdarabjának perdülete ![\[\Delta\vec{N}_i=\vec{r}_i\times\Delta\vec{p}_i=\Delta m_i\vec{r}_i\times\vec{v}_i=\Delta m_i\vec{r}_i\times\left(\vec{\omega}\times\vec{r}_i\right)\]](/images/math/1/1/6/1161049c21349ce905ad4b31094a4105.png)
 - és
- és  -rányú komponenseinek változását, ezért csak a perdület
-rányú komponenseinek változását, ezért csak a perdület  -irányú komponensével kell foglalkoznunk:
-irányú komponensével kell foglalkoznunk: ![\[\Delta N_{z_i}=\Delta m_i\omega_z R_i^2\]](/images/math/a/0/c/a0cfbce96590422e1f8224db79de2337.png)
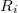 a tömegpont távolsága a tengelytől (4. ábra). A test teljes perdületének
a tömegpont távolsága a tengelytől (4. ábra). A test teljes perdületének  -komponense
-komponense ![\[N_z=\sum_i\Delta m_i\omega_z R_i^2=\omega_z\sum_i\Delta m_i R_i^2\]](/images/math/a/a/2/aa2ec022732aa4e5fd56ccbf95334bdb.png)
![\[\Theta_z=\sum_i\Delta m_i R_i^2\]](/images/math/d/4/d/d4d4ead403307048eca6a3ab2fcc39e4.png)
 -irányú perdülete így:
-irányú perdülete így: ![\[N_z=\Theta_z\omega_z\]](/images/math/4/0/0/4000d1729a78a404e3b01ada39b66d79.png)
![\[M_z=\frac{{\rm d}N_z}{{\rm d}t}=\frac{{\rm d}\left(\Theta_z\omega_z\right)}{{\rm d}t}=\Theta_z\frac{{\rm d}\omega_z}{{\rm d}t}=\Theta_z\beta_z\]](/images/math/3/a/2/3a2e131134fc1df4eeebb468d6fa387d.png)
 -irányú forgatónyomaték nulla, akkor a test állandó szögsebességgel forog:
-irányú forgatónyomaték nulla, akkor a test állandó szögsebességgel forog: ![\[M_z=0\quad\Leftrightarrow\quad\omega_z={\rm const.}\]](/images/math/b/3/e/b3e4947f4bd504881883c415efbcd3bf.png)
![\[E_m=\sum_i\frac{1}{2}\Delta m_i v_i^2=\frac{1}{2}\sum_i\Delta m_i\left(\omega R_i\right)^2=\frac{1}{2}\omega^2\sum_i\Delta m_i R_i^2=\frac{1}{2}\Theta\omega^2\]](/images/math/e/2/5/e2508a447c46cda1d94805b812a875e8.png)
Precesszió
A pörgettyű olyan forgó test, melynek egyetlen pontja rögzített, amely körül szabadon foroghat.
Ha a pörgettyűre nem hat külső forgatónyomaték (pl. ha a rögzített pont a test tömegközéppontja), akkor perdületvektora időben állandó. Ez az ún. erőmentes pörgettyű. A perdületvektor állandóságán alapul a giroszkóp működése, melyet repülőgépekben (mesterséges horizont) és űrhajókban használnak a jármű orientációjának érzékelésére és szabályozására.
Ha a pörgettyűre külső forgatónyomaték hat (pl. tömegközéppontja alatt vagy felett van alátámasztva), akkor súlyos pörgettyűről beszélünk. Ilyen eszköz a gyerekjátékként használt búgócsiga. A gyorsan megpörgetett búgócsiga (annak ellenére, hogy a tömegközéppontja alatt van alátámasztva) nem dől fel, hanem forgástengelye egy függőleges tengelyű kúp mentén lassan körbefordul. Ez a mozgás a precesszió.
A precesszió jelensége az 5. ábra alapján megérthető: a gyorsan forgó, forgásszimmetrikus pörgettyűre a nehézségi erő forgatónyomatéka hat. A perdület és a forgatónyomaték közti kapcsolat![\[\Delta\vec{N}=\vec{M}\Delta t\]](/images/math/6/3/f/63fa226f5951b3f8dcffb7f2df12754c.png)
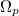 precessziós szögsebességgel körbefordul. A forgatónyomaték, a precesszió szögsebessége és a pörgettyű perdülete közötti kapcsolat
precessziós szögsebességgel körbefordul. A forgatónyomaték, a precesszió szögsebessége és a pörgettyű perdülete közötti kapcsolat ![\[\vec{M}=\vec{\Omega}_p\times\vec{N}\]](/images/math/a/0/b/a0b6f10943f1fbe780b00039fce0ed0d.png)
Forgómozgás a hétköznapokban és a természetben
Gyorsan forgó adathordozók a számítógépben
A merevlemez és a DVD a számítógép két fontos adathordozója: az írható és olvasható adatokat mindkettőben – egészen különböző módon – gyorsan forgó lemezek tárolják. A nagy adatsűrűség és a minél gyorsabb adatelérés rendkívül gyors forgást tesz szükségessé, ami – a kis méretekkel együtt – komoly technikai kihívást jelent.
A mai merevlemezek 5400-15000 fordulat/perc sebességgel forognak. A tükörsima lemezek 10-20 nm vastag mágneses rétegei felett néhány tized nm távolságra, egy néhány atom vastagságú légpárnán siklik az író-olvasó fej – a lemez pereménél versenyautónál is nagyobb sebességgel. Emiatt a lemezeket speciális pormentes helyiségekben kell összeszerelni és légmentesen lezárni. Az adatok írása az írófejben létrehozott mágneses térrel történik, a kiolvasásnál viszont a hagyományos indukciós elven működő apró tekercs helyett már az óriás mágneses ellenállás (GMR) kvantummechanikai jelenségén alapuló eszközöket használnak (ezzel jelentősen megnövelve az elérhető adatsűrűséget és kiolvasási sebességet).
A DVD lemezek szintén akár 10000 fordulat/perc sebességgel foroghatnak. Az író és olvasó lézerfényt ilyen sebesség mellett kell a  m-nél kisebb „lyukakba” fókuszálni.
m-nél kisebb „lyukakba” fókuszálni.
Forgómozgás a sportban
A forgómozgásnak nagyon sok sportágban van meghatározó szerepe. A gerelyhajításnál, a diszkoszvetésnél és a frizbinél a forgásnak fontos szerepe van az eldobott test repülési helyzetének stabilizálásában. Az eldobáskor megforgatott sportszerek megőrzik perdületüket, és így olyan helyzetben maradnak, hogy az aerodinamikai felhajtóerő miatt sokkal messzebbre repülnek.
Ugyanez a szerepe a lövedékek forgásának is. A (sport)fegyverek csövében található huzagolás a kirepülő lőszert nagy sebességgel megforgatja hossztengelye körül, ezzel biztosítva stabilitását.
A labdajátékoknál is fontos szerepe van a forgásnak, de itt nem a helyzet stabilitása miatt: a forogva repülő labdára a levegővel való kölcsönhatás miatt a közegellenálláson kívül oldalirányú erő is hat (Magnus-effektus), ami a labda pályáját oldalirányban eltéríti. Ennek köszönhetően lehet szögletből közvetlenül gólt lőni. A pingpongban a nyesett és csavart labdák pedig nem csak a levegőben, hanem az asztalról való visszapattanáskor is „furcsán” viselkednek.
A perdületmegmaradás tételére szép példa a piruettező mozgása: a korcsolyázó vagy a tornász kitárt karokkal és térddel (azaz nagy tehetetlenségi nyomatékkal kezd forogni. Amikor karjait, lábát behúzza, a tehetetlenségi nyomatéka lecsökken, és így a perdület állandósága miatt (lábujjhegyen vagy a korcsolya hegyén pörögve nagyon kicsi a külső forgatónyomaték) a szögsebessége megnő, pörögni kezd.
Bonyolult forgó mozgás a szaltó és a különböző szertorna gyakorlatok: a forgás sebessége itt is a végtagok behúzásával gyorsítható.
A biciklikerekek forgására később visszatérünk.
A Föld precessziója: a csillagjegyek eltolódása
A Föld forgástengelye nem merőleges az ekliptikára (az ekliptika a Föld keringési síkja), hanem a merőlegestől 23,5°-kal eltér. Ez a tengelyferdeség okozza az évszakok változását: nyáron az északi féltekén a napfény meredekebben éri a felszínt, mint télen, így erősebb a besugárzás.
A Nap látszólagos mozgása az égen bonyolultabb, mint a csillagoké: egyrészt a Föld forgása miatt naponta felkel és lenyugszik, másrészt a keringés miatt a delelés látszólagos helye az égbolton folyamatosan változik. Azok a csillagképek, amelyeken egy év alatt végighalad a Nap delelése az állatövi csillagképek. A Nap látszólagos pályája kétszer keresztezi az egyenlítőt (ilyenkor a nappalok és az éjszakák hossza megegyezik), ezek közül egyik a tavaszpont. A forgástengely meghosszabbítása északi irányban egy aránylag fényes csillag közelében halad el: ez a Sarkcsillag. A Sarkcsillag mindig ugyanott látható az égbolton, ezért jól használható tájékozódásra.
A Föld azonban nem gömbszimmetrikus: a forgás miatt alakja jó közelítéssel lapult forgási ellipszoid. Emiatt a Nap (és a Hold) gravitációs erejének forgatónyomatéka van, amely a Föld tengelyét az ekliptikára merőleges irányba próbálja beforgatni.
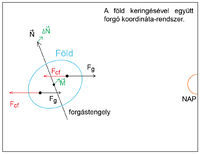
A jelenséget érdemes a Föld keringésével együtt forgó koordinátarendszerből vizsgálni: ebben a koordinátarendszerben a Föld középpontja nyugalomban van, viszont a Földre a Nap gravitációs erején kívül a (fiktív) centrifugális erő is hat.![\[F_g=\gamma\frac{m_F m_N}{r^2}\]](/images/math/0/2/3/023028133bbebeb0f3014080d73f0003.png)
![\[F_cf=\omega^2 r\]](/images/math/6/0/8/6081197b93abb05752d46944963161ad.png)
A Föld középpontjában a két erő kiegyenlíti egymást (hiszen ebben a koordinátarendszerben a Föld középpontja nyugalomban van). A Föld Naphoz közelebbi felén azonban az erők távolságfüggése miatt 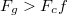 , míg a távolabbi felén
, míg a távolabbi felén 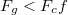 (6. ábra). Az így kialakuló erőpárnak a Föld perdületére merőleges forgatónyomatéka van, ezért a forgó Föld tengelye a búgócsigához hasonlóan precesszálni fog.
(6. ábra). Az így kialakuló erőpárnak a Föld perdületére merőleges forgatónyomatéka van, ezért a forgó Föld tengelye a búgócsigához hasonlóan precesszálni fog.
A precesszió periódusideje kb. 26000 év. Ez azt jelenti, hogy az ókor óta a csillagjegyek kb. egy hónappal eltolódtak (pl. a tavaszpont már nem a kos csillagképbe esik). A precesszió miatt változik a forgástengely meghosszabbításának a helye is az égbolton: a Sarkcsillag csak a jelenkorban van az égi pólus közelében.
A forgástengely precessziója mellett megfigyelhető a tengelyferdeség lassú változása is: a tengelyferdeség mértéke 41000 éves periódussal ingadozik 22° és 24,5° között, ami jelentősen befolyásolja a Föld éghajlatát.
A Hold-pálya precessziója: miért nincs minden hónapban napfogyatkozás?
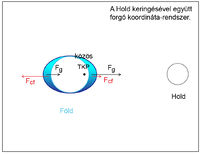
A Hold keringésének síkja nem egyezik meg az ekliptikával, azzal kb. 5°-os szöget zár be. A Hold-pályára a forgó Földhöz hasonlóan hat a Nap forgatónyomatéka, ezért a Hold-pálya tengelye is precesszál (18,6 éves periódusidővel).
Napfogyatkozás újholdkor lehet (amikor a Hold a Nap és a Föld között van), holdfogyatkozás pedig teliholdkor (amikor a Hold és a Nap a Föld két ellentétes oldalán van). A fogyatkozásoknak azonban az is feltétele, hogy a Hold éppen az ekliptika közelében legyen, ezért nincs minden hónapban fogyatkozás. A lehetséges időpontokat a Föld és a Hold keringéséből, valamint a Hold-pálya precessziójából adódó ciklusok határozzák meg. A fogyatkozás létrejötte és jellege, valamint megfigyelhetősége ezen kívül függ még a Nap-Föld és a Föld-Hold távolságtól, és természetesen a megfigyelő földrajzi helyétől (és az időjárástól) is. Holdfogyatkozást aránylag gyakran lehet látni, hiszen ha a Hold a Föld árnyékába kerül, akkor azt a Föld minden olyan pontjáról látni lehet, ahonnan a Hold látszik (tehát kb. a Föld feléről, ahol éppen éjszaka van). A teljes napfogyatkozás egy adott földrajzi helyen azért olyan ritka, mert a Hold látszólagos átmérője kb. megegyezik a Nap látszólagos átmérőjével (0,5°), és így a Hold árnyékkúpja csak egy nagyon kis területen éri el a Földet. (Amikor a Hold földtávolban, a Föld pedig napközelben van, akkor pedig egyáltalán nem éri el: ilyenkor csak gyűrűs napfogyatkozás látható.) A fogyatkozás során ez az árnyékkúp halad végig egy keskeny sávon, ahonnan a teljes napfogyatkozás megfigyelhető.
A Hold mozgására hatással vannak a Föld-Hold rendszerben kialakuló árapály erők. Az árapály jelenséget a Föld-Hold rendszerrel együtt forgó koordinátarendszerben érdemes vizsgálni: A Hold és a Föld a közös tömegközéppont körül kering (ami a tömegarányok miatt a Föld belsejébe esik). A forgó koordinátarendszerben az égitestekre a gravitációs vonzáson kívül a centrifugális erő is hat. Az Föld középpontjában a Hold vonzása és a centrifugális erő kiegyenlíti egymást (hiszen ebben a koordinátarendszerben nyugalomban van). A Hold felé néző oldalon a gravitációs erő, az ellentétes oldalon pedig a centrifugális erő nagyobb, így ezeken a helyeken az óceánok felszíne megemelkedik.
A Föld forgása miatt ezek a kiemelkedések körbejárják a Földet, így egy adott helyen naponta kétszer dagály, kétszer pedig apály figyelhető meg. (A Holdon kívül a Nap is hozzájárul az árapály-jelenséghez, amit a kontinensek is jelentősen befolyásolnak, így annak nagysága nagyon különböző: néhány cm-től akár 20 m-ig is változik.) A Földön körbehaladó dagályhullám fékezi a Föld forgását (emiatt lassan nő a napok hossza), ez viszont a rendszer összperdületének állandósága miatt a Hold pályaperdületének növekedését, és így a Földtől való folyamatos távolodást okozza.
A Holdon a tömegarányok miatt sokkal erősebb árapály erők lépnek fel. Mivel jelenleg a Holdon nincs folyékony anyag ezek az erők csak holdrengéseket okoznak. Korábban viszont az árapály erők fékezése lassította a Hold forgását, egészen addig, amíg a forgási idő meg nem egyezett a keringési idővel. Ez a kötött forgás az oka annak, hogy a Holdnak mindig ugyanazt az oldalát látjuk. (A Hold billegése miatt azonban a felszín 59 %-a látható a Földről.)
Látványos kísérletek
A perdületmegmaradást bemutató kísérleti videók után néhánytovábbi szép kísérlet:
A lejtőn leguruló testek mozgását befolyásolja a testek tehetetlenségi nyomatéka. Az azonos átmérőjű, de különböző tehetetlenségi nyomatékú testek (tömör henger, üreges henger, golyó) más-más gyorsulással gördülnek le a lejtőn.
A következő videón egy pörgettyű viselkedését tanulmányozhatjuk. Ha a kerék nem forog, akkor, ha a tömegközéppontja felett van alátámasztva, fizikai ingaként viselkedik, ha a tömegközéppontja alatt, akkor ledől, ha pedig a tömegközéppontjában, akkor közömbös egyensúlyi helyzetben van.
A megpörgetett kerék másképp viselkedik: ha nem a tömegközéppontjában van alátámasztva, akkor precesszálni fog. A precesszió iránya attól függ, hogy a kerék a tömegközéppontja alatt avgy felett van alátámasztva (hiszen ettől függ a pörgettyűre ható forgatónyomaték iránya). A tömegközéppontjában alátámasztott (ún. erőmentes) pörgettyű nem precesszál.
Két további videón azt lehet megfigyelni, hogy a szabadon (nem rögzített tengely körül) forgó testek csak bizonyos meghatározott tengelyek körül foroghatnak.
Egy tévhit: miért lehet biciklizni?
Széles körben elterjedt tévhit, hogy azért lehet biciklizni, mert a biciklikeréknek perdülete van, és ez stabilizálja a feldőléssel szemben. A bicikli azonban azért nem dől fel, mert már csekély dőléskor is a kormány elfordul a dőlés irányába, és az emiatt körpályára kényszerített biciklire ható centrifugális erő (a jelenséget a biciklivel együtt kanyarodó, azaz forgó rendszerből leírva) a dőlő biciklit felállítja.
Az igaz, hogy a kerék perdülete miatt a bicikli dőlésekor fellépő pörgettyűnyomaték közrejátszik a kormány elfordításában, de ez a hatás – különösen könnyű kerekű bicikliknél – sokkal kisebb, mint a kerék utánfutása miatt fellépő forgatónyomaték. Ez utóbbi hatásról könnyen meggyőződhetünk, ha egy álló biciklit a nyergénél megfogunk, és kicsit megdöntjük: a kormány el fog fordulni a dőlés irányába (annak ellenére, hogy az álló keréknek nincs perdülete). Ennek az az oka, hogy a kormány tengelyének meghosszabbítása az első kerék érintkezési pontja előtt metszi a talajt (a két pont távolságát nevezik utánfutásnak), és így a megdöntött biciklinél a talaj által kifejtett kényszererőnek forgatónyomatéka van a kormány tengelyére vonatkoztatva.
A biciklizés fizikája röviden és részletesebben.
Vissza a Fizika 1i nyitóoldalára
1. Tér és idő
3. Megmaradási törvények a mechanikában
4. Rezgések
6. Hideg-meleg