„Erőtan I. - 2.1.2” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Kinematika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 16. sor: | 16. sor: | ||
<wlatex>#: a) Az emelés időtartamát $T$-vel jelöljük. A végsebesség így $v_{1}=aT$ a magasság pedig $H=\frac{a}{2}T^{2}$ alakban írhatók. $$T=\frac{v_{1}}{a}$$ $$H=\frac{v_{1}^{2}}{2a} \qquad\Rightarrow\qquad a=\frac{v_{1}^{2}}{2H}=2\,\mathrm{\frac{m}{s^{2}}}$$ | <wlatex>#: a) Az emelés időtartamát $T$-vel jelöljük. A végsebesség így $v_{1}=aT$ a magasság pedig $H=\frac{a}{2}T^{2}$ alakban írhatók. $$T=\frac{v_{1}}{a}$$ $$H=\frac{v_{1}^{2}}{2a} \qquad\Rightarrow\qquad a=\frac{v_{1}^{2}}{2H}=2\,\mathrm{\frac{m}{s^{2}}}$$ | ||
#: b) A mozgatás során a testre ható erők az általunk kifejtett $F$ erő (felfelé) és a gravitációs erő (lefelé). Az eredő erő $$F_{e}=F-F_{g}=ma \qquad\Rightarrow\qquad F=m(a+g)=192 \,\mathrm{N}$$ | #: b) A mozgatás során a testre ható erők az általunk kifejtett $F$ erő (felfelé) és a gravitációs erő (lefelé). Az eredő erő $$F_{e}=F-F_{g}=ma \qquad\Rightarrow\qquad F=m(a+g)=192 \,\mathrm{N}$$ | ||
| − | #: c) A mozgatás | + | #: c) A mozgatás időtartama az a) rész alapján $$T=\frac{2H}{v_{1}}=3\,\mathrm{s}\,.$$ Az utolsó másodpercben a sebesség egyenletesen nőtt $4\,\mathrm{\frac{m}{s}}$-ról $6\,\mathrm{\frac{m}{s}}$-ra, tehát az átlagsebesség $5\,\mathrm{\frac{m}{s}}$ volt. |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 12., 17:58-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Erőtan I. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
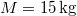tömegű terhet álló helyzetből egyenletesen gyorsítva függőlegesen 
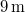magasságra emelünk.
- a) Mekkora a gyorsulás, ha a végsebesség
?
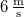- b) Mekkora erő szükséges a mozgatáshoz?
- c) Mennyi ideig tart a mozgás és mekkora az átlagsebesség az utolsó másodpercben?
- a) Mekkora a gyorsulás, ha a végsebesség
Megoldás
- a) Az emelés időtartamát
-vel jelöljük. A végsebesség így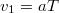 
a magasság pedig 
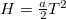alakban írhatók. ![\[T=\frac{v_{1}}{a}\]](/images/math/6/a/1/6a1b122c7b4fa79a75e4630570167555.png)
![\[H=\frac{v_{1}^{2}}{2a} \qquad\Rightarrow\qquad a=\frac{v_{1}^{2}}{2H}=2\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/a/2/0/a204da5391947c468f011f3084f4396d.png)
- b) A mozgatás során a testre ható erők az általunk kifejtett
erő (felfelé) és a gravitációs erő (lefelé). Az eredő erő ![\[F_{e}=F-F_{g}=ma \qquad\Rightarrow\qquad F=m(a+g)=192 \,\mathrm{N}\]](/images/math/8/3/b/83bd923f360ae76229189fa886e74ff4.png)
- c) A mozgatás időtartama az a) rész alapján Az utolsó másodpercben a sebesség egyenletesen nőtt
![\[T=\frac{2H}{v_{1}}=3\,\mathrm{s}\,.\]](/images/math/3/3/2/3327e4dec33d0d8efbdb6de2e3e2d5cb.png)
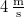-ról 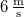-ra, tehát az átlagsebesség 
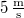volt.
- a) Az emelés időtartamát
