Mechanika - Rezgések I.
A Fizipedia wikiből
Feladatok
- (1.4.35.) Határozzuk meg a pont
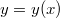 pályaegyenletét, ha a koordináták időfüggése:
pályaegyenletét, ha a koordináták időfüggése:
- a)
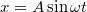 ;
; 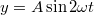
- b)
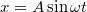 ;
; 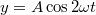 ÚtmutatásEjtsük ki az időkoordinátát.Végeredmény
ÚtmutatásEjtsük ki az időkoordinátát.Végeredmény![\[y^2=4x^2\left(1-\frac{x^2}{A^2}\right)\]](/images/math/7/6/5/7658dc4d2c1288cf7145f37bf6b7a8dd.png)
![\[y=A\left(1-\frac{2x^2}{A^2}\right)\]](/images/math/a/2/3/a23d0d74ec791e34f38a01a870c58d71.png)
- a)
- (2.1.24.)
 tömegű testet
tömegű testet  rugóállandójú súlytalan rugóra akasztunk. A testet kezdősebesség nélkül elengedjük abban a helyzetben, amelyben a rugó feszültségmentes. Adjuk meg a kitérést az idő függvényében!ÚtmutatásÁllapítsuk meg az egyensúlyi helyzetet és ahhoz képest a kezdeti feltételeket!Végeredmény
rugóállandójú súlytalan rugóra akasztunk. A testet kezdősebesség nélkül elengedjük abban a helyzetben, amelyben a rugó feszültségmentes. Adjuk meg a kitérést az idő függvényében!ÚtmutatásÁllapítsuk meg az egyensúlyi helyzetet és ahhoz képest a kezdeti feltételeket!Végeredmény![\[x(t)=\frac{mg}k(1-\cos(\omega t))\]](/images/math/c/6/c/c6c3d4785fff01b27c7d2bf78ad2e67a.png)
- (2.1.49.) Pontszerűnek tekinthető
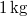 tömegű testre
tömegű testre 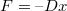 erő hat. A rugóállandó:
erő hat. A rugóállandó: 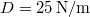 . A
. A  pillanatban a kitérés
pillanatban a kitérés 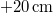 , a sebesség
, a sebesség 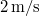 és a nagysága növekszik.
és a nagysága növekszik.
- a) Mekkora a rezgés frekvenciája?
- b) Mekkora a rezgés amplitúdója?
- c) Írja fel a helyzet-idő függvényt! Mekkora a kezdőfázis?Végeredmény
![\[\omega=5\,\frac1{\rm s}\]](/images/math/2/4/1/241b9e387a43c0c9dab921fc625ac8be.png)
![\[A=0,448\,\rm m\]](/images/math/4/1/d/41d391a8a1b54956ae327869b2e3471e.png)
![\[x(t)=\cos(\omega t+63,4^{\circ})\]](/images/math/4/b/a/4bad91bd0424aa424e0ee839d1e58112.png)
- (6.1.) Egy részecske
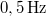 frekvenciával harmonikus rezgőmozgást végez. A
frekvenciával harmonikus rezgőmozgást végez. A  időpillanatban
időpillanatban 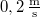 sebességgel halad át az egyensúlyi helyzetén. Írja fel a helyzet-idő függvényt a konkrét adatokkal!Végeredmény
sebességgel halad át az egyensúlyi helyzetén. Írja fel a helyzet-idő függvényt a konkrét adatokkal!Végeredmény![\[x(t)=\frac{0,2}{\pi}\sin{\pi t}\]](/images/math/c/f/0/cf01d6f79d01f041f81b1bd652893a4c.png)
- (6.5.) Az
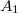 amplitúdóval és
amplitúdóval és 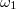 frekvenciával vízszintes síkon rezgő
frekvenciával vízszintes síkon rezgő  tömegű testre az egyensúlyi helyzeten áthaladva felülről
tömegű testre az egyensúlyi helyzeten áthaladva felülről  tömegű agyagdarab esik, mely rátapad. Mekkora lesz az új rezgésidő és az amplitúdó?Végeredmény
tömegű agyagdarab esik, mely rátapad. Mekkora lesz az új rezgésidő és az amplitúdó?Végeredmény![\[T_2=T_1\sqrt{\frac{m+M}m}\]](/images/math/5/2/9/5299745e574e83530e82dc3f461dc9a9.png)
![\[A_2=A_1\sqrt{\frac m{m+M}}\]](/images/math/6/c/d/6cd5224246932e436be28cbb9c9c6be6.png)
- (6.6.) Egy
 tömegű kosár
tömegű kosár  direkciós erejű rugón nyugszik. A kosár felett
direkciós erejű rugón nyugszik. A kosár felett  magasságból
magasságból  tömegű testet ejtünk le, amely rugalmatlanul ütközve a kosárban marad. Milyen amplitúdóval fog rezegni a kosár?ÚtmutatásNe felejtsük el figyelembe venni az egyensúlyi helyzet eltolódását!Végeredmény
tömegű testet ejtünk le, amely rugalmatlanul ütközve a kosárban marad. Milyen amplitúdóval fog rezegni a kosár?ÚtmutatásNe felejtsük el figyelembe venni az egyensúlyi helyzet eltolódását!Végeredmény![\[A^2=\frac{m^2g^2}{k^2}\left(1+\frac{2kh}{g(m+M)}\right)\]](/images/math/1/e/8/1e8c79c1281603308099e98f7b455a8a.png)
- (*6.9.) Két vízszintes helyzetű
 rugóállandójú rugó közé
rugóállandójú rugó közé  tömegű anyagi pontot erősítünk, amely vertikálisan kis amplitúdóval rezgéseket végez. A két rugó összhossza nyugalmi állapotban
tömegű anyagi pontot erősítünk, amely vertikálisan kis amplitúdóval rezgéseket végez. A két rugó összhossza nyugalmi állapotban 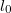 , megfeszítve
, megfeszítve  . Határozzuk meg a rezgési frekvenciát, mint
. Határozzuk meg a rezgési frekvenciát, mint  függvényét, ha kis amplitúdójú rezgéseket engedünk csak meg. Vizsgáljuk az
függvényét, ha kis amplitúdójú rezgéseket engedünk csak meg. Vizsgáljuk az 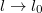 határesetet! ÚtmutatásÍrjuk fel a rugó hosszváltozásás pontosan a Pitagorasz-tétel segítségével, majd közelítsük kis változásokra. Ne felejtsük el a rugóerőt a mozgás irányára vetíteni!VégeredményAz effektív rugóállandóezzel számolható a frekvencia az ismert összefüggéssel.
határesetet! ÚtmutatásÍrjuk fel a rugó hosszváltozásás pontosan a Pitagorasz-tétel segítségével, majd közelítsük kis változásokra. Ne felejtsük el a rugóerőt a mozgás irányára vetíteni!VégeredményAz effektív rugóállandóezzel számolható a frekvencia az ismert összefüggéssel.![\[D_{\rm{eff}}=D\frac{l-l_0}l,\]](/images/math/8/6/8/868de616f0bc7382d57a8f8ed809d15a.png)
- (*6.11.) Mutassuk meg, hogy egy kúpinga periódusideje ugyanakkora, ha egy kis kör mentén mozog, mint ha síkban kis lengéseket végez!VégeredményA körfrekvencia négyzete mindkét esetben
![\[\omega^2=\frac gl\]](/images/math/e/8/6/e869d041559ef36b3aab46f5685284e8.png)
- (*6.14.) Az ábrán látható
 tömegű test a vízszintes rúdon súrlódás nélkül mozoghat. A hozzá kapcsolódó rugó másik végpontját a rúdtól
tömegű test a vízszintes rúdon súrlódás nélkül mozoghat. A hozzá kapcsolódó rugó másik végpontját a rúdtól  távolságra rögzítjük. A rugó nyugalmi hossza
távolságra rögzítjük. A rugó nyugalmi hossza 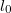 , rugóállandója
, rugóállandója  . Határozzuk meg az egyensúlyi helyzet körüli kis rezgések frekvenciáját különböző
. Határozzuk meg az egyensúlyi helyzet körüli kis rezgések frekvenciáját különböző  távolságok esetén! Vizsgáljuk meg a
távolságok esetén! Vizsgáljuk meg a 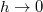 és
és 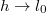 határeseteket! ÚtmutatásÍrjuk fel a rugó hosszváltozásás pontosan a Pitagorasz-tétel segítségével, majd közelítsük kis változásokra. Ne felejtsük el a rugóerőt a mozgás irányára vetíteni!VégeredményAz effektív rugóállandóezzel számolható a frekvencia az ismert összefüggéssel.
határeseteket! ÚtmutatásÍrjuk fel a rugó hosszváltozásás pontosan a Pitagorasz-tétel segítségével, majd közelítsük kis változásokra. Ne felejtsük el a rugóerőt a mozgás irányára vetíteni!VégeredményAz effektív rugóállandóezzel számolható a frekvencia az ismert összefüggéssel.![\[D_{\rm{eff}}=D\frac{l_0^2-h^2}{l_0^2},\]](/images/math/2/6/0/2609eb153ada82b39c411e744dc94731.png)
- (*6.16.) Vízszintes lapon álló
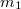 és
és 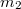 tömegű kiskocsikat
tömegű kiskocsikat  rugóállandójú rugóval kötünk össze. A két kiskocsit széthúzzuk, majd hirtelen elengedjük őket. Hogyan fognak ezután mozogni? (A súrlódástól eltekintünk.)ÚtmutatásLássuk be, hogy a két test kitérés-idő függvénye egymás számszorosa, majd ezt használjuk ki az egymásba helyettesítésüknél a két csatolt mozgásegyenletben!Végeredmény
rugóállandójú rugóval kötünk össze. A két kiskocsit széthúzzuk, majd hirtelen elengedjük őket. Hogyan fognak ezután mozogni? (A súrlódástól eltekintünk.)ÚtmutatásLássuk be, hogy a két test kitérés-idő függvénye egymás számszorosa, majd ezt használjuk ki az egymásba helyettesítésüknél a két csatolt mozgásegyenletben!Végeredmény![\[\omega^2=D\frac{m_1+m_2}{m_1m_2}\]](/images/math/9/7/0/9702e7a0db656030d1694b915dcaf52e.png)
- (*6.19.) Határozzuk meg az
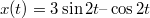 törvény szerint harmonikus rezgőmozgást végző tömegpont mozgásának amplitúdóját és periódusidejét!ÚtmutatásHasználjunk trigonometrikus azonosságokat a függvény átalakításához!Végeredmény
törvény szerint harmonikus rezgőmozgást végző tömegpont mozgásának amplitúdóját és periódusidejét!ÚtmutatásHasználjunk trigonometrikus azonosságokat a függvény átalakításához!Végeredmény![\[T=\pi\]](/images/math/3/5/1/351957643fac8c9b2300a903bf445973.png)
![\[A=\sqrt{10}\]](/images/math/e/a/2/ea290d6fbddc61784f2ce57aad007d80.png)
- (*6.20.) Egyik harmonikus rezgés amplitúdója
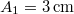 , kezdőfázisa
, kezdőfázisa 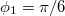 , a másiké
, a másiké 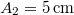 ,
, 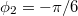 . Mekkora az eredő amplitúdó és az előálló rezgés fázisállandója?ÚtmutatásHasználjunk forgóvektorokat vagy komplex amplitúdókat az összegzéshez!Végeredmény
. Mekkora az eredő amplitúdó és az előálló rezgés fázisállandója?ÚtmutatásHasználjunk forgóvektorokat vagy komplex amplitúdókat az összegzéshez!Végeredmény![\[A=7\,\rm{cm}\]](/images/math/c/0/4/c048db28d95c52173bbbfe48b07c71b4.png)
![\[\alpha=-8,2^{\circ}\]](/images/math/2/4/6/2467e7b19fe9b6006446b6033f8cd45f.png)
- (*6.21.) Azonos frekvenciájú, egyirányú rezgések összetevésénél az egyik rezgés amplitúdója
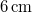 , kedzőfázisa
, kedzőfázisa 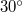 , a másik rezgés amplitúdója
, a másik rezgés amplitúdója 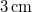 .
.
- a) Mekkorára kell választani a második rezgés kezdőfázisát, hogy az eredő rezgés kezdőfázisa zérus legyen?
- b) Mekkora lesz ebben az esetben az eredő rezgés amplitúdója?
- c) Mekkorára kell a második rezgés kezdőfázisát választani, hogy az eredő amplitúdó
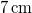 legyen?Végeredmény
legyen?Végeredmény![\[\phi_2=-90^{\circ}\]](/images/math/e/c/0/ec061405b2af353cbb01bd290cfaffcc.png)
![\[A_2\approx5,2\,\rm{cm}\]](/images/math/4/0/a/40ab8bda66808c9d377f14602032956e.png) vagy
vagy![\[\phi_2=-53,6^{\circ}\]](/images/math/b/2/8/b28b28672baadb71c868b28a2630c068.png)
![\[\phi_2=113,6^{\circ}\]](/images/math/c/c/8/cc8c4bdf40a85ac72d7923fd1cc92415.png)
- (*6.22.) Két, azonos amplitúdójú rezgés, melyek frekvenciája
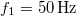 és
és 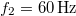 egyszerre kezdi meg rezgését az egyensúlyi helyzetből. Mikor lesz legelőször ismét azonos a kitérésük?Végeredmény
egyszerre kezdi meg rezgését az egyensúlyi helyzetből. Mikor lesz legelőször ismét azonos a kitérésük?Végeredmény![\[t=4,54\,\rm{ms}\]](/images/math/8/6/2/862159a61d26c02e62478ef5e33e8c42.png)
- (6.24.) Két egyirányú harmonikus rezgés eredője:
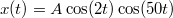 , ahol
, ahol  másodpercekben értendő. Mekkora az összetevő rezgések frekvenciája, és mekkora a lebegés frekvenciája?ÚtmutatásAlakítsuk át a függvényt trigonometrikus függvények összegére!Végeredmény
másodpercekben értendő. Mekkora az összetevő rezgések frekvenciája, és mekkora a lebegés frekvenciája?ÚtmutatásAlakítsuk át a függvényt trigonometrikus függvények összegére!Végeredmény![\[f_l=0,636\,\rm{Hz}\]](/images/math/f/8/c/f8c9411ace4847d35dd0b4c6319cb3f0.png)