Mechanika - Merev testek II.
A Fizipedia wikiből
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
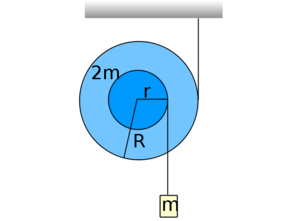
- (*3.3.5.)
tömegű, 
sugarú, függőleges tengely körül súrlódás nélkül forgó korong kerületén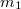 
tömegű pontszerű test van rögzítve. A rendszer 
szögsebességgel forog. Mekkora munka árán lehet az 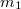tömegpontot a forgástengelyhez hozni? (A tömegpontot pl. súrlódásmentes csatornában húzzuk a centrum felé.)Végeredmény![\[W=\frac12\omega^2m_1R^2\left(\frac{2m_1}m+1\right)\]](/images/math/c/2/8/c28609ebe704254142dd1a0500b2ae41.png)
- (3.3.6.) sugarú tömegű korong kerületére csavart fonál végét rögzítjük, és a korongot elengedjük.
- a) Írjuk le a korong mozgását!
- b) Mekkora a korong szögsebessége és középpontjának
sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról 
hosszúságú fonaldarab csavarodott le? 
Végeredmény![\[\beta=\frac{2g}{3R}\]](/images/math/c/6/a/c6af796891b7a163698d29903524966c.png)
![\[K=\frac{mg}3\]](/images/math/5/2/7/52725fae775e2fae11b0ff221c1c53ea.png)
![\[\omega=\sqrt{\frac{4gl}{3R^2}}\]](/images/math/5/9/d/59d2cc5504905104ac1e8e187ab1e258.png)
![\[v=\sqrt{\frac43 gl}\]](/images/math/5/7/a/57a92411e8d0a4b01ec5b3e9920a3958.png)
- (*3.3.7.) sugarú
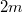tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű 
sugarú tárcsa kerületére csavart fonál végére tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását! 
Végeredmény![\[\beta=g\frac{6R-2r}{8R^2+2r^2-4rR}\]](/images/math/4/c/b/4cb2890bf3e7604cd4b163ff532dedb8.png)
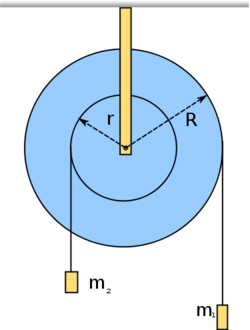
- (*3.3.8.) Az ábrán feltüntetett
tehetetlenségi nyomatékú lépcsős csiga két kötelére 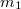és 
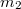tömegű súlyokat függesztünk. Határozzuk meg a csiga szöggyorsulását, és a kötélágakban ébredő erőket! 
Végeredmény![\[\beta=\frac{m_1gR-m_2gr}{m_1R^2+m_2r^2+\theta}\]](/images/math/a/6/b/a6b10a5a3ca6e0c94124a48c3fde35ee.png)
- (*3.3.9.) Vízszintes tengely körül forgó csigán átvetett fonál egyik végén tömegű teher függ. A fonál másik vége rugóhoz csatlakozik, amelynek rugóállandója
. A csiga sugara , tehetetlenségi nyomatéka . Mutassuk ki, hogy a teher rezgőmozgást végez! Mekkora a rezgésidő?
ÚtmutatásVigyázzunk, hogy a kötél két szakaszának eltérő a feszítettsége!Végeredmény![\[T=2\pi\sqrt{\frac{\frac{\theta}{R^2}+m}{D}}\]](/images/math/6/2/9/629305006f9afd82df6c9355df5b3d49.png)
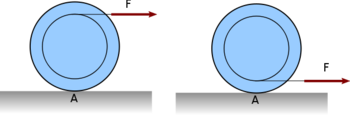
- (*3.3.13.) Vízszintes lapon álló tömegű koronghoz erősített elhanyagolható tömegű tárcsa kerületére csavart fonalat vízszintes irányban állandó
erővel húzunk. A korong sugara , a tárcsa sugara .(A fonalat a korong középpontja fölött húzzuk.) 
- a) Mekkora gyorsulással mozog a korong középpontja?
- b) Mi a talaj és a korong között fellépő súrlódási erő szerepe a korong középpontjának gyorsításánál?
- c) Mekkora
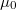súrlódási együttható szükséges ahhoz, hogy a korong a talajon csúszás nélkül gördülhessen?
- d) Oldjuk meg a feladatot arra az esetre is, ha a fonalat a korong középpontja alatt húzzuk a talaj síkjával párhuzamosan! ÚtmutatásVegyünk fel tetszőleges irányú súrlódási erőt a rajzon, mivel ez az erő ismeretlen. A rajznak megfelelően kell viszont az egygenletekben előjelet kapnia Gördülésnél a súrlódási erő tapadási.VégeredményA súrlódási erő iránya kétféle is lehet
![\[a=\frac{2F(R+r)}{3mR}\]](/images/math/1/4/f/14fea7cbad5e618c0756bb75b048707c.png)
-től függően. ami akár nulla is lehet. A d) esetben![\[F\frac{|R-2r|}{3R}\leq\mu mg\]](/images/math/7/b/3/7b3f8a0e7226f4f01df5aa6a3c52b70c.png)
A súrlódási erő mindig fékező.![\[a=\frac{2F(R-r)}{3mR}\]](/images/math/7/1/b/71be2975663507fcc3303251e984602c.png)
![\[F\frac{R+2r}{3R}\leq\mu mg\]](/images/math/6/3/2/632ce9fdb826c13954fc7e4d49edcf26.png)
- (*3.3.16.) Egy
hajlásszögű lejtőre tömegű és sugarú hengert helyezünk, majd magára hagyjuk.
- a) Hogyan fog a henger mozogni, ha a lejtő és a hengerfelület között nem lép fel súrlódás?
- b) Mekkora lesz az a minimális 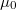súrlódási tényező, melynél a henger tisztán gördül a lejtőn? Határozza meg a tiszta gördülés esetén a mozgást jellemző mennyiségeket!
- c) Mekkora lesz a henger szögsebessége a
magasságú lejtő alján?
- d) Írja le a henger mozgását olyan esetben, amikor
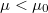!ÚtmutatásVigyázzunk, hogy a különféle esetekben hogyan kezeljük a súrlódási erőt!VégeredményTisztán lecsúszikgyorsulással. A tisztán legördülés esetéhez![\[a=g\sin{\alpha}\]](/images/math/b/c/7/bc7929481f8e308534ecbc3567aaade1.png)
kell, és![\[\frac13\tan{\alpha}\leq\mu\]](/images/math/c/c/f/ccf677356ca0210480e6698d61fcf18c.png)
A d) esetben csúszva gördül![\[a=\frac23g\sin{\alpha}\]](/images/math/f/4/0/f404a0436088f24f08d5d2b0bc3cae08.png)
és![\[a=g(\sin{\alpha}-\mu\cos{\alpha})\]](/images/math/5/c/2/5c22ae9a55d2d0901faeef6e02296926.png)
valamint![\[\beta=\frac{2\mu g\cos{\alpha}}R\]](/images/math/3/3/b/33b132b73a5d4827e4645de72e6fd92b.png)
![\[\beta R<a\]](/images/math/d/7/2/d72caf56dca3e9b6ef6bcd2c1228fdd7.png)
- (3.3.17.) A vízszintessel
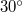-os szöget képező 
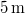magasságú lejtőn egyidejűleg kezdősebesség nélkül elindítunk egy hasábot, egy hengert és egy golyót. A hasáb súrlódásmentesen csúszik, a henger és a golyó csúszásmentesen gördül. A testek különböző időtartamok alatt érnek a lejtő aljára, ahol lécbe ütköznek. Mekkora időközök telnek el az egyes ütközések között?VégeredményA keresett időközök
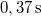és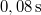 
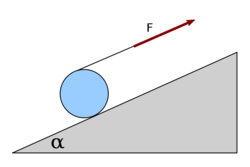
- (*3.3.18.) sugarú, tömegű homogén körhenger kerületére fonalat csavarunk. A hengert ezután hajlásszögű lejtőre helyezzük. A hengert elengedve a fonalat erővel húzzuk felfelé. Mekkora kötélerő biztosítja azt, hogy a henger csak forgó mozgást végezzen?
Végeredmény![\[F=mg\sin{\alpha}-\mu mg\cos{\alpha}\]](/images/math/7/0/5/7053a1cfa75a0c8d1a8fd84533bdbfd2.png)
- (*3.3.24. alapján) Egy pontszerűnek tekinthető
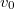sebességű 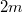tömegű hokikorong tökéletesen rugalmatlanul ütközik egy fele akkora tömegű, hosszúságú rúd végével (jégen). Az ütközés után a testek összetapadnak. Írja le a rendszer mozgását ütközés után! 
- a) Hol lesz az ütközés után a rendszer tömegközéppontja (a rúd hossza mentén)?
- b) Mekkora lesz a tömegközéppont sebessége?
- c) Mekkora az e pontra vonatkoztatott tehetetlenségi nyomaték?
- d) Milyen szögsebességgel forog a rendszer ütközés után?ÚtmutatásMerev testek tökéletesen rugalmatlan ütközésekor a két test "összetapad", és csak az impulzus meg az impulzusmomentum marad meg.VégeredményA rúd végétől
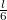, a rúd tömegközéppontjától pedig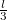 
![\[v_{\rm{TKP}}=\frac23v_0\]](/images/math/5/d/5/5d5396ddab117439c0ca159e066f4fc2.png)
![\[\theta=\frac{ml^2}4\]](/images/math/8/0/0/8004f12e9022f79533b290c126599250.png)
![\[\omega=\frac{4v_0}{3l}\]](/images/math/9/d/9/9d97c81c85d0ac5361b502ca65bdfcec.png)
- Oldjuk meg az előző feladatot abban az esetben, ha az ütközés tökéletesen rugalmas!VégeredményMajd lesz.
- (*3.3.29.) Egy 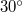hajlásszögű lejtőre
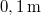magasságú, 
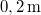hosszú és 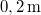szélességű testet helyezünk. A test tömege 
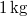. A test és a lejtő felülete között a súrlódási tényező 
.
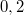- a) Írja fel a test mozgásegyenletét!
- b) Hol van a test és a lejtő kölcsönhatását számbavevő erők támadáspontja?
- c) Létezhet-e akkora súrlódási tényező, hogy a test felbillenjen?ÚtmutatásA tömegközéppont kettő és a forgás egy mozgásegyenletét általánosan érdemes felírni, majd azokat az eseteket vizsgálni, amikor a test nem billen, hanem csúszik vagy tapad. A súrlódási erő minimum/maximum feltételei megadják a különböző esetek fennállásának feltételétVégeredményEz az test ezen a lejtőn nem billenhet fel.
![\[t=\mu b=0,02\,m\]](/images/math/f/3/0/f301bbccc865b474c54d78aa482358ec.png)
