„Kinematika - 1.4.6” változatai közötti eltérés
A Fizipedia wikiből
| 12. sor: | 12. sor: | ||
$$v_{y}(t)=\frac{dy}{dt}=0$$$$v_{z}(t)=\frac{dz}{dt}=-2ct$$ $$a_{x}(t)=\frac{dv_{x}}{dt}=2a$$ $$a_{y}(t)=\frac{dv_{y}}{dt}=0$$ $$a_{z}(t)=\frac{dv_{z}}{dt}=-2c$$$$T=\frac{1}{\sqrt{5}}\,\mathrm{s}$$}}</wlatex></includeonly><noinclude> | $$v_{y}(t)=\frac{dy}{dt}=0$$$$v_{z}(t)=\frac{dz}{dt}=-2ct$$ $$a_{x}(t)=\frac{dv_{x}}{dt}=2a$$ $$a_{y}(t)=\frac{dv_{y}}{dt}=0$$ $$a_{z}(t)=\frac{dv_{z}}{dt}=-2c$$$$T=\frac{1}{\sqrt{5}}\,\mathrm{s}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex># A tömegpont $y$-irányban nem mozdul el, ezért a mozgás során végig az $xz$-síkban halad. Az $x=at^2$ és $z=b-ct^{2}$ egyenletek egyikéből kifejezve az időt, a másikba behelyettesítve meghatározhatjuk a tömegpont pályáját $$z=b-\frac{c}{a}x\,,$$ amely egy egyenest ír le. A helykoordináták időfüggése alapján a pont sebességének komponensei az alábbiak szerint számolhatók ki. $$v_{x}(t)=\frac{dx}{dt}=2at$$ | + | <wlatex># A tömegpont $y$-irányban nem mozdul el, ezért a mozgás során végig az $xz$-síkban halad. Az $x=at^2$ és $z=b-ct^{2}$ egyenletek egyikéből kifejezve az időt, a másikba behelyettesítve meghatározhatjuk a tömegpont pályáját $$z=b-\frac{c}{a}x\,,$$ amely egy egyenest ír le. A helykoordináták időfüggése alapján a pont sebességének komponensei az alábbiak szerint számolhatók ki. $$v_{x}(t)=\frac{dx}{dt}=2at$$$$v_{y}(t)=\frac{dy}{dt}=0$$$$v_{z}(t)=\frac{dz}{dt}=-2ct$$ A gyorsulás pedig $$a_{x}(t)=\frac{dv_{x}}{dt}=2a$$ $$a_{y}(t)=\frac{dv_{y}}{dt}=0$$ $$a_{z}(t)=\frac{dv_{z}}{dt}=-2c$$ <br> Az $x$-tengelynél a $t=0$ pillanatban van. A feladat szerint meg kell határoznunk, hogy ezután mennyi idő telik el, míg a tömegpont eléri a $z$-tengelyt, vagyis mikor lesz $z=0$. $$z(T)=0\qquad\Rightarrow\qquad T=\sqrt{\frac{b}{c}}=\frac{1}{\sqrt{5}}s$$ |
| − | $$v_{y}(t)=\frac{dy}{dt}=0$$$$v_{z}(t)=\frac{dz}{dt}=-2ct$$ A gyorsulás pedig $$a_{x}(t)=\frac{dv_{x}}{dt}=2a$$ $$a_{y}(t)=\frac{dv_{y}}{dt}=0$$ $$a_{z}(t)=\frac{dv_{z}}{dt}=-2c$$ <br> Az $x$-tengelynél a $t=0$ pillanatban van. A feladat szerint meg kell határoznunk, hogy ezután mennyi idő telik el, míg a tömegpont eléri a $z$-tengelyt, vagyis mikor lesz $z=0$. $$z(T)=0\qquad\Rightarrow\qquad T=\sqrt{\frac{b}{c}}=\frac{1}{\sqrt{5}}s$$ | + | |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 11., 08:43-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Kinematika |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy mozgó pont helyvektorának komponensei:
, 
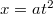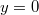és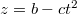 
. Határozzuk meg a pont pályáját, sebességét és gyorsulását, valamint azt az időtartamot, amely alatt a pont a pályának a koordináta-tengelyek közötti szakaszát megteszi. Legyen például: 
, 
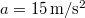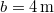és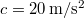 
.
Megoldás
- A tömegpont
-irányban nem mozdul el, ezért a mozgás során végig az 
-síkban halad. Az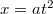 
és 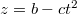egyenletek egyikéből kifejezve az időt, a másikba behelyettesítve meghatározhatjuk a tömegpont pályáját amely egy egyenest ír le. A helykoordináták időfüggése alapján a pont sebességének komponensei az alábbiak szerint számolhatók ki.![\[z=b-\frac{c}{a}x\,,\]](/images/math/e/b/a/eba67d17cc483593b57267f6b96505a2.png)
![\[v_{x}(t)=\frac{dx}{dt}=2at\]](/images/math/e/c/5/ec5a9a0f6aa65e5f9c123c0e560c6080.png)
![\[v_{y}(t)=\frac{dy}{dt}=0\]](/images/math/8/c/e/8cecc42d71c399cdfd95e9b2432f3374.png)
A gyorsulás pedig![\[v_{z}(t)=\frac{dz}{dt}=-2ct\]](/images/math/b/5/5/b55c511a3c496794e1561599ce3f5669.png)
![\[a_{x}(t)=\frac{dv_{x}}{dt}=2a\]](/images/math/3/b/a/3ba61228431454ebf2c3bb9e3061726f.png)
![\[a_{y}(t)=\frac{dv_{y}}{dt}=0\]](/images/math/8/6/c/86cf03285f52a55c0c9e82111950f622.png)
![\[a_{z}(t)=\frac{dv_{z}}{dt}=-2c\]](/images/math/1/1/6/116e9872f2717798b24eba10b43cf067.png)
Az
-tengelynél a 
pillanatban van. A feladat szerint meg kell határoznunk, hogy ezután mennyi idő telik el, míg a tömegpont eléri a 
-tengelyt, vagyis mikor lesz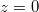 
. ![\[z(T)=0\qquad\Rightarrow\qquad T=\sqrt{\frac{b}{c}}=\frac{1}{\sqrt{5}}s\]](/images/math/c/f/c/cfc3af32467dd9b6daa5ed3f0d6c7d6c.png)
