„Erőtan I. - 2.1.38” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Erőtan I. {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 9. sor: | 9. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Az $\alpha$ hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel $\varphi$ szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható $\mu<\mbox{tg}\,\alpha\cos\varphi/(1+\mbox{tg}\,\alpha\sin\varphi)$? | </noinclude><wlatex># Az $\alpha$ hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel $\varphi$ szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható $\mu<\mbox{tg}\,\alpha\cos\varphi/(1+\mbox{tg}\,\alpha\sin\varphi)$? | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=Először a | + | </wlatex><includeonly><wlatex>{{Útmutatás|content=Először a lejtővel párhuzamos és arra merőleges komponensekre bontsd fel az erőket! Ezután a párhuzamos síkban bontsd fel léccel párhuzamos és lécre merőleges komponensre!}}{{Végeredmény|content= $$a=g\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]$$ }}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>#: A testre ható gravitációs erőt először lejtőre merőleges ($F_{g1}=mg\cos\varphi$) és azzal párhuzamos komponensre bontjuk fel ($F_{g2}=mg\sin\alpha$). A lejtőre merőleges irányban nem történik mozgás ezért a lejtő $N=mg\cos\alpha$ nyomóerővel nyomja a testet. A lejtővel párhuzamos síkban a gravitációs erő $F_{g2}$ nagyságú komponensét felbontjuk egy a lécre merőleges ($F_{g21}=mg\sin\alpha\cos\varphi$) és a léccel párhuzamos irányú komponensre ($F_{g22}=mg\sin\alpha\sin\varphi$). Ebben a síkban a lécre merőleges irányban sincs mozgás, ezért a léc a testet $N'=F_{g21}$ erővel nyomja. A léccel párhuzamos irányba a mozgásegyenlet $$ma=F_{g22}-S-S'\,,$$ amely meghatározza a test gyorsulását és ahol $S$ a lejtő által kifejtett súrlódási erő, míg $S'$ a léc által kifejtett súrlódási erő. $$S=\mu N\qquad S'=\mu N' \qquad\qquad ma=mg\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]$$ A gyorsulás tehát $$a=g\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]\,.$$ | <wlatex>#: A testre ható gravitációs erőt először lejtőre merőleges ($F_{g1}=mg\cos\varphi$) és azzal párhuzamos komponensre bontjuk fel ($F_{g2}=mg\sin\alpha$). A lejtőre merőleges irányban nem történik mozgás ezért a lejtő $N=mg\cos\alpha$ nyomóerővel nyomja a testet. A lejtővel párhuzamos síkban a gravitációs erő $F_{g2}$ nagyságú komponensét felbontjuk egy a lécre merőleges ($F_{g21}=mg\sin\alpha\cos\varphi$) és a léccel párhuzamos irányú komponensre ($F_{g22}=mg\sin\alpha\sin\varphi$). Ebben a síkban a lécre merőleges irányban sincs mozgás, ezért a léc a testet $N'=F_{g21}$ erővel nyomja. A léccel párhuzamos irányba a mozgásegyenlet $$ma=F_{g22}-S-S'\,,$$ amely meghatározza a test gyorsulását és ahol $S$ a lejtő által kifejtett súrlódási erő, míg $S'$ a léc által kifejtett súrlódási erő. $$S=\mu N\qquad S'=\mu N' \qquad\qquad ma=mg\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]$$ A gyorsulás tehát $$a=g\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]\,.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 12., 21:27-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Erőtan I. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Az
 hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel
hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel  szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható
szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható 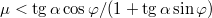 ?
?
Megoldás
- A testre ható gravitációs erőt először lejtőre merőleges (
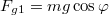 ) és azzal párhuzamos komponensre bontjuk fel (
) és azzal párhuzamos komponensre bontjuk fel (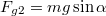 ). A lejtőre merőleges irányban nem történik mozgás ezért a lejtő
). A lejtőre merőleges irányban nem történik mozgás ezért a lejtő 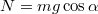 nyomóerővel nyomja a testet. A lejtővel párhuzamos síkban a gravitációs erő
nyomóerővel nyomja a testet. A lejtővel párhuzamos síkban a gravitációs erő 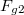 nagyságú komponensét felbontjuk egy a lécre merőleges (
nagyságú komponensét felbontjuk egy a lécre merőleges (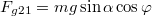 ) és a léccel párhuzamos irányú komponensre (
) és a léccel párhuzamos irányú komponensre (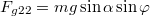 ). Ebben a síkban a lécre merőleges irányban sincs mozgás, ezért a léc a testet
). Ebben a síkban a lécre merőleges irányban sincs mozgás, ezért a léc a testet 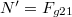 erővel nyomja. A léccel párhuzamos irányba a mozgásegyenlet amely meghatározza a test gyorsulását és ahol
erővel nyomja. A léccel párhuzamos irányba a mozgásegyenlet amely meghatározza a test gyorsulását és ahol![\[ma=F_{g22}-S-S'\,,\]](/images/math/6/7/c/67c3ab9275f54d04a98578dcb2827ce1.png)
 a lejtő által kifejtett súrlódási erő, míg
a lejtő által kifejtett súrlódási erő, míg 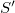 a léc által kifejtett súrlódási erő. A gyorsulás tehát
a léc által kifejtett súrlódási erő. A gyorsulás tehát![\[S=\mu N\qquad S'=\mu N' \qquad\qquad ma=mg\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]\]](/images/math/7/2/d/72d563f6e0154f8c5c01e34594816f92.png)
![\[a=g\left[\sin\alpha\cos\varphi-\mu\left(\cos\alpha+\sin\alpha\sin\varphi\right)\right]\,.\]](/images/math/8/b/0/8b094c7dfffc24435d5a899dac6e8e79.png)
- A testre ható gravitációs erőt először lejtőre merőleges (