„Mechanika - Mozgástan” változatai közötti eltérés
A Fizipedia wikiből
| 4. sor: | 4. sor: | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| gyaksorszám = 3 | | gyaksorszám = 3 | ||
| − | | témakör = | + | | témakör = Mozgástan |
}} | }} | ||
A lap 2013. április 11., 11:25-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mozgástan |
| Feladatok listája: Sablon:Mozgástan: Feladatok listája |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- (*1.1.7.) Két párhuzamosan haladó sínpáron egy-egy vonat halad egymás felé. Az egyik vonat sebessége
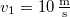, a másiké 
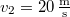. A gyorsabban haladó vonat füttyjelet bocsát ki, melyet a vonat vezetője 
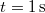hosszúnak észlel. Milyen hosszúnak méri a füttyjelet a töltésen álló, illetve a közeledő vonaton ülő megfigyelő? (hangsebesség: 
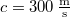)Végeredmény![\[t_{km}=\frac{28}{30}\,\mathrm{s}\]](/images/math/d/a/a/daadb30d0aab190625d6fd66baa88fdf.png)
![\[t_{mv}=\frac{28}{31}\,\mathrm{s}\]](/images/math/3/c/8/3c88c5c2a4af314c492b65bf4b02918c.png)
- (1.2.6.) Egy testet függőleges irányban
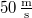sebességgel feldobunk. Milyen magasra emelkedik 
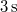alatt? Mekkora a legnagyobb magasság, amit elér? Mennyi ideig emelkedik felfelé? Mennyi idő múlva esik vissza a földre? (
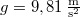)Végeredmény![\[h(t_{1})=105,855\,\mathrm{m}\]](/images/math/9/8/0/98006297470c3b6a5492750401e2cc9d.png)
![\[T_{\mathrm{em}}=5,097\,\mathrm{s}\]](/images/math/f/c/4/fc4b2acaadc3fbe34913ee8d0e2baafe.png)
![\[h_{\mathrm{max}}=127,42\,\mathrm{m}\]](/images/math/1/7/9/17984e9c807af34b17790258c4a8d6b8.png)
![\[T_{\mathrm{ve}}=10,194\,\mathrm{s}\]](/images/math/5/2/e/52e8a22c2c21feb15a2804f220e62446.png)
- (*1.2.8.) Egy motorkerékpáros állandó
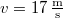sebességgel halad el a rendőr előtt, aki azonnal észreveszi, hogy a motoros bizonyos szabálysértést követett el, és ezért utol kell érnie. Négy másodperccel később a rendőr üldözni kezdi a motorost, állóhelyből indulva, és állandó gyorsulással mozogva. őrhelyétől mérve 
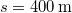távolságban éri utól a motorost. Mennyi időt fordított a rendőr az üldözésre? Mekkora volt a gyorsulása? Mekkora sebességgel haladt a rendőr a motoros beérésekor?Végeredmény![\[T=19,53 \,\mathrm{s}\]](/images/math/6/7/e/67e546ecf8d513edc22e4504b00714da.png)
![\[a=2,1\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/3/6/c/36c0fa90d182327b93e378ca5470e33a.png)
![\[v_{max}=41,01\,\mathrm{\frac{m}{s}}\]](/images/math/0/5/0/050a276a092dc2b99b00a3db34b36698.png)
- (**1.2.17, csak csemegének) Egy
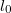hosszúságú, tökéletesen rugalmas és korlátlanul nyújtható fonál egyik végét falhoz rögzítjük. Erről a végpontról a fonálon mászva 
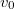sebességgel elindul egy hangya a másik vége felé. Ugyanabban a pillanatban azonban egy gonosz manó 
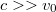állandó sebességgel elkezdi húzni a fonál szabad végét. A hangyának a fonálhoz viszonyított sebessége az egész mozgás során állandó. Utolérheti-e a hangya a manót? (Mi történik, ha a hangya a manótól indul a fal felé?)ÚtmutatásEgy általános
időpontban határozzuk meg a fonál hosszát! Tegyük fel, hogy a hangya ekkor 
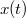helyen van. Írjuk fel ekkor a sebességet és a gyorsulást a külső megfigyelő rendszerében! VégeredményA hangya mindig utoléri a hangyát, és eléri a falat is.
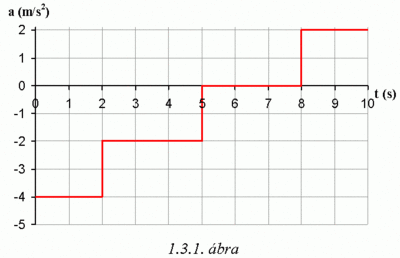
- (1.3.1) Az
tengelyen mozgó tömegpont gyorsulása az idő függvényében az 1.3.1. ábrán látható.
- a) Ábrázolja a tömegpont sebességét az idő függvényében, ha a kezdeti sebesség
!
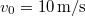- b) Határozza meg a tömegpont helyét a
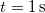és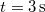 
időpillanatokban, ha a tömegpont 
-ban az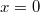 
pontban volt!
- c) Mekkora a tömegpont átlagsebessége 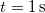a és a 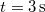közötti időintervallumban?
Végeredményb)c)![\[x(t=1\,\mathrm{s})=8\,\mathrm{m}\qquad\mbox{és}\qquad x(t=3\,\mathrm{s})=13\,\mathrm{m}\]](/images/math/1/d/9/1d92104ff21ed0f944a94dd313184e0b.png)
![\[v_{\mbox{átl}}=2,5\,\mathrm{\frac{m}{s}}\]](/images/math/0/1/5/0151fed8f7ee34d0bac7b4dddd29ba0c.png)
- a) Ábrázolja a tömegpont sebességét az idő függvényében, ha a kezdeti sebesség
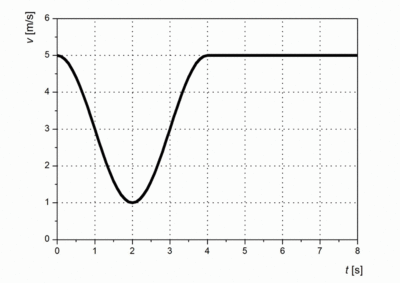
- (*1.2.22) Egy test a vizsgált időtartam első felében harmonikus rezgést végez, a második felében egyenletesen mozog. Mozgásának sebesség-idő grafikonja az alábbi ábrán látható.
- a) Írja fel a sebességet az idő függvényében mindkét tartományon!
- b) Határozza meg a gyorsulás-idő függvényt képlettel!
- c) Határozza meg az 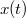függvényt, ha a test a
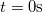időpillanatban az origóban volt!
- (*1.3.8.) Egy részecske a pozitív tengely irányába mozog, úgy, hogy sebessége az alábbi törvény szerint változik: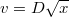
, ahol d pozitív állandó. Tételezzük fel, hogy a időpontban a részecske az origóban volt. Határozzuk meg
- a) a részecske sebességének és gyorsulásának függését az időtől!
- b) a részecske átlagsebességét, míg az 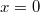pontból az
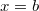pontba jut!ÚtmutatásA
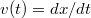összefüggés alapján írjuk fel az 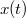függvényre vonatkozó differenciál egyenletet! Végeredménya)b)![\[v(t)=\frac{dx}{dt}=\frac{D^{2}t}{2}\qquad\mbox{és}\qquad a(t)=\frac{dv}{dt}=\frac{D^{2}}{2}\,.\]](/images/math/5/c/3/5c35932b8b593f4579cfad4df4ec0f57.png)
![\[v_{atlag}=\frac{b}{T}=\frac{D\sqrt{b}}{2}\,.\]](/images/math/3/3/5/3357662062e58205cc30d3b9e3c4f776.png)
- (1.4.6) Egy mozgó pont helyvektorának komponensei:
, 
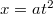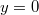és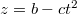 
. Határozzuk meg a pont pályáját, sebességét és gyorsulását, valamint azt az időtartamot, amely alatt a pont a pályának a koordináta-tengelyek közötti szakaszát megteszi. Legyen például: 
, 
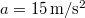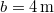és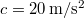 
.ÚtmutatásA pálya meghatározásához fejezd ki az időt valamely helykoordináta segítségével! A gyorsulás kiszámításához deriváld le kétszer a helyvektort az idő szerint!Végeredmény![\[v_{x}(t)=\frac{dx}{dt}=2at\]](/images/math/e/c/5/ec5a9a0f6aa65e5f9c123c0e560c6080.png)
![\[v_{y}(t)=\frac{dy}{dt}=0\]](/images/math/8/c/e/8cecc42d71c399cdfd95e9b2432f3374.png)
![\[v_{z}(t)=\frac{dz}{dt}=-2ct\]](/images/math/b/5/5/b55c511a3c496794e1561599ce3f5669.png)
![\[a_{x}(t)=\frac{dv_{x}}{dt}=2a\]](/images/math/3/b/a/3ba61228431454ebf2c3bb9e3061726f.png)
![\[a_{y}(t)=\frac{dv_{y}}{dt}=0\]](/images/math/8/6/c/86cf03285f52a55c0c9e82111950f622.png)
![\[a_{z}(t)=\frac{dv_{z}}{dt}=-2c\]](/images/math/1/1/6/116e9872f2717798b24eba10b43cf067.png)
![\[T=\frac{1}{\sqrt{5}}\,\mathrm{s}\]](/images/math/4/7/a/47a615343d494770a174a8c68461644d.png)
- (*1.4.7 alapján) Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le:
.
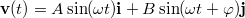- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
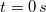időpontban a test az 
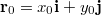koordinátájú pontban tartózkodott!
- b) Határozza meg a test gyorsulásvektorát az idő függvényében!
- c) Milyen pályán mozog a test, ha
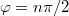valamilyen 
egész számmal?
- d) Amennyiben
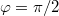, úgy adjuk meg a pálya görbületi sugarát a 
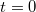időponthoz tartozó helyen.ÚtmutatásA sebességet integrálva megkaphatjuk a tömegpont helyzetének időfüggését. Ügyeljünk a kezdeti feltételre.Végeredménya)b)![\[\mathbf{r}(t)=\left(x_{0}+\frac{A}{\omega}-\frac{A}{\omega}\cos(\omega t)\right)\mathbf{i} +\left( y_{0}+\frac{B}{\omega}\cos\varphi- \frac{B}{\omega}\cos(\omega t+\varphi)\right)\mathbf{j}\]](/images/math/f/6/0/f6040af91a503d71c967cfcd88b7ad15.png)
c) Ha![\[\mathbf{a}(t)=\frac{d\mathbf{v}}{dt}=A\omega\cos(\omega t)\mathbf{i} + B\omega\cos(\omega t+\varphi)\mathbf{j}\]](/images/math/7/7/3/773077855448f6930e66c3cd3d40a012.png)
páratlan, akkor ellipszis, ha páros, akkor egyenes. d)![\[ \phantom{a} \]](/images/math/9/4/3/943e36a2c1f8ac3b616b1b6f372704ca.png)
![\[R = \frac{B^2}{A \omega} \]](/images/math/4/c/d/4cdb0376f93d4374b0de665d21cb013e.png)
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
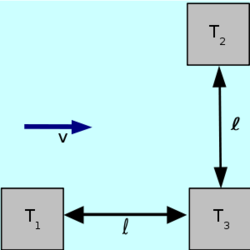
- (*1.4.10) Folyóvízben három tutaj van lehorgonyozva.
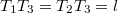, irányuk egymásra merőleges. A víz 
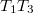irányában folyik 
sebességgel. Két gyorsúszó azonos, a vízhez képest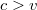 
sebességgel a 
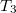tutajról egyszerre indulnak, az egyik a 
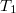a másik a 
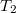felé, ezeket megérintve visszatérnek 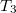-hoz. Melyik ér vissza előbb, és mennyivel késik a másik? 
ÚtmutatásGondoljuk át, hogy a kettes számú tutaj felé úszó ember pontosan merre is úszik különböző megfigyelők szerint!VégeredményA 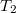tutajról induló úszó hamarabb ér vissza a tutajra.
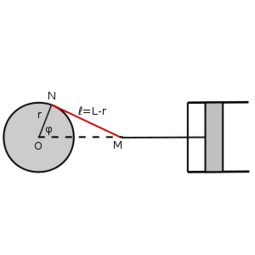
- (*1.4.17) Egy gőzgép hajtókereke egyenletes
szögsebességgel forog az 
középpontján átmenő tengely körül. A kerék 
hosszúságú hajtórúdjának 
csuklópontja az -tól 
távolságban van, 
vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az pont sebessége abban a pillanatban, amikor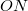 
a vízszintessel 
szöget zár be? ( a dugattyú-karral egy egyenesen fekszik.)
ÚtmutatásAz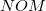
háromszögre cosinus-tételt alkalmazzunk! Végeredmény![\[v(\varphi)=r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{l^{2}-r^{2}\sin^{2}\varphi}}\right]\]](/images/math/6/0/9/6092a2866d0201a1853d0abdba7e6e76.png)
- (1.4.18) Egy vékony egyenes cső pontja körül állandó szögsebességgel forog vízszintes síkban. A csőben egy golyó mozog a csőhöz képest állandó 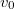sebességgel. Milyen pályát ír le a golyó a csövön kívül álló megfigyelőhöz képest és mekkora a sebesség nagysága, mint az idő függvénye?
ÚtmutatásHasználj polárkoordinátákat!Végeredmény![\[x(t)=r(t)\cos\varphi(t)=|r_{0}-v_{0}t|\cos(\omega t)\]](/images/math/1/b/5/1b54f1253d5a11bc70d46623d4bc8d3f.png)
![\[y(t)=r(t)\sin\varphi(t)=|r_{0}-v_{0}t|\sin(\omega t)\]](/images/math/0/1/2/01251920eb548f27d48bedaeac6bce78.png)
![\[v_{x}(t)=\frac{dx}{dt}=v_{0}\,\mathrm{sgn}(v_{0}t-r_{0})\cos(\omega t)-\omega|r_{0}-v_{0}t|\sin(\omega t)\]](/images/math/c/6/8/c68477d3eb2712b303f188963a7ca762.png)
![\[v_{y}(t)=\frac{dy}{dt}=v_{0}\mathrm{sgn}\,(v_{0}t-r_{0})\sin(\omega t)+\omega|r_{0}-v_{0}t|\cos(\omega t)\]](/images/math/f/2/5/f250fb4680228cdc9488be1131f2a783.png)
- (*1.4.20) Egy ember a tó partján sétálva a tóban egy fuldoklót vesz észre. A fuldokló a parttól
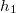, az ember 
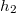távolságban van. A fuldokló és a mentésére siető távolsága 
. Milyen úton haladjon a mentésre siető ember, hogy a fuldoklót leghamarabb elérje, ha a parton futva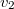 
, a vízben úszva 
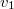sebességgel tud haladni?
- (*1.4.23) Egy aknavetővel a völgyből
magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége .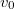 
Végeredmény![\[\varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}\]](/images/math/c/b/3/cb3a2e723a373e2c2b55afd5e5011270.png)
![\[D=\frac{v_{0}^{2}}{g}-2h\,.\]](/images/math/6/4/9/64909bf4299497b17ab066ed1374ca88.png)
