Mechanika - Mozgástan - 1.1.7

Feladat

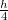1. (*3.2.6.) Mekkora egy $\setbox0\hbox{$h$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú pálca lengésideje, ha a felső végétől $\setbox0\hbox{$\frac{h}4$}% \message{//depth:\the\dp0//}% \box0%$ távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?

Megoldás

A megadott forgástengely a tömegközépponttól is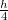 $\setbox0\hbox{$\frac{h}4$}% \message{//depth:\the\dp0//}% \box0%$ távolságra van, így a Steiner-tétel szerint a rá vonatkozó tehetetlenségi nyomaték

$\[\theta=\frac1{12}mh^2+m\left(\frac{h}4\right)^2=\frac7{48}mh^2.\]$

A végponti tehetetlenségi nyomatékból kiindulni helytelen lett volna, mert sem az, sem a megadott forgáspont nem tömegközéppont! A tömegközéppontban ható súlyerő forgatónyomatéka

$\[M(\alpha)=mg\frac{h}4sin\alpha\approx mg\frac{h}4\alpha\]$

a kis szögek miatt. Ezzel a mozgásegyenlet

$\[-mg\frac{h}4\alpha=\frac7{48}mh^2\ddot\alpha,\]$

egyszerűsítve

$\[\ddot\alpha=-\frac{12g}{7h}\alpha=-\omega^2\alpha,\]$

azaz valóban a harmonikus rezgés mozgásegyenletét kaptuk. Ebből a rezgés körfrekvenciáját leolvasva a periódusidőre adódik

$\[T=2\pi\sqrt{\frac{7h}{12g}}\]$

.