Erőtan I. - 2.1.48
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 12., 21:27-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Erőtan I. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
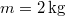 tömegű anyagi pontra
tömegű anyagi pontra 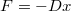 alakú rugalmas erő hat.
alakú rugalmas erő hat. 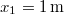 távolságban az erő nagysága
távolságban az erő nagysága 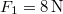 . A kezdő időpontban
. A kezdő időpontban 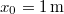 és
és 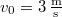 . Határozzuk meg a pont mozgását az idő függvényében!
. Határozzuk meg a pont mozgását az idő függvényében!
Megoldás
- A rugóállandó
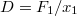 szerint számolható ki. A tömegpont mozgásegyenlete A gyorsulás éppen az elmozdulás második időszerinti deriváltja, melyet
szerint számolható ki. A tömegpont mozgásegyenlete A gyorsulás éppen az elmozdulás második időszerinti deriváltja, melyet![\[ma=-Dx\,.\]](/images/math/0/2/3/023d7370c3105ed4ddbc480a3f2714f8.png)
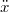 szerint jelölünk. Így a mozgásegyenlet a differenciálegyenletre vezet, ahol bevezettük az
szerint jelölünk. Így a mozgásegyenlet a differenciálegyenletre vezet, ahol bevezettük az![\[\ddot{x}+\omega^{2}x=0\]](/images/math/e/4/c/e4cbe78d632e327d100f5e67cb27ceca.png)
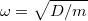 körfrekvenciát. A differenciál egyenlet két független megoldása
körfrekvenciát. A differenciál egyenlet két független megoldása 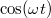 és
és 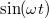 , melyek mindketten egy harmonikus rezgőmozgást írnak le. A differenciálegyenlet lineáris, ezért az általános megoldás ezek tetszőleges lineáris kombinációjaként, azaz a sebesség pedig
, melyek mindketten egy harmonikus rezgőmozgást írnak le. A differenciálegyenlet lineáris, ezért az általános megoldás ezek tetszőleges lineáris kombinációjaként, azaz a sebesség pedig![\[x(t)=A\cos(\omega t)+B\sin(\omega t)\,,\]](/images/math/a/b/1/ab1084f3e60f33ef5e183d9e6d291b66.png) Az
Az![\[v(t)=\dot{x}(t)=-A\omega\sin(\omega t)+B\omega\cos(\omega t)\,.\]](/images/math/a/9/6/a96064d238f1ddd1152b5261e4cf892a.png)
 és
és  együtthatókat a kezdeti feltételek segítségével határozhatjuk meg.
együtthatókat a kezdeti feltételek segítségével határozhatjuk meg. ![\[x(0)=x_{0}\qquad\Rightarrow\qquad A=x_{0}\]](/images/math/4/d/8/4d86a91deb45ee9e302d0e43fd4a3994.png) Ezek alapján megadható a pont mozgása.
Ezek alapján megadható a pont mozgása.![\[v(0)=v_{0}\qquad\Rightarrow\qquad B\omega=v_{0}\]](/images/math/a/1/0/a1011f23d15562d64ee0f67eb95715e3.png)
![\[x(t)=x_{0}\cos(\omega t)+\frac{v_{0}}{\omega}\sin(\omega t)\]](/images/math/f/c/b/fcb491f28cdc69f6c4d34ab258021eac.png)
![\[x_{0}=1\,\mathrm{m}\qquad v_{0}=3\,\mathrm{\frac{m}{s}}\qquad \omega=\sqrt{\frac{F_{1}}{x_{1}m}}=2\frac{1}{s}\]](/images/math/8/3/c/83c69081f83ece6d6b7c4b065a57a5c2.png)
- A rugóállandó
![\[x(t)=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}\left[\frac{x_{0}}{\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}}\cos(\omega t)+ \frac{\frac{v_{0}}{\omega}}{\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}}\sin(\omega t)\right]\]](/images/math/0/3/4/034843193a91eb3efc417e99e9b968f7.png)
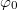 fázist, melyre
fázist, melyre ![\[\mbox{tg}\,\varphi_{0}=\frac{v_{0}}{\omega x_{0}}\,.\]](/images/math/5/9/b/59bfd7b1f4d2f9bded51a474eaae146a.png)
![\[x(t)=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}\left[\cos\varphi_{0}\cos(\omega t)+\sin\varphi_{0}\sin(\omega t)\right]=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}\cos(\omega t-\varphi_{0})\]](/images/math/5/0/e/50e79f56f21dd3197e47a2415a061607.png)