Erőtan I. - 2.1.14
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 12., 20:50-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Erőtan I. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
 hajlásszögű lejtő tetejéről a
hajlásszögű lejtő tetejéről a  időpontban elengedünk egy
időpontban elengedünk egy  tömegű testet, ugyanakkor el is kezdjük húzni a lejtővel párhuzamosan
tömegű testet, ugyanakkor el is kezdjük húzni a lejtővel párhuzamosan 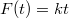 nagyságú erővel felfelé. A mozgást addig vizsgáljuk, míg a test újra meg nem áll. Numerikus adatok :
nagyságú erővel felfelé. A mozgást addig vizsgáljuk, míg a test újra meg nem áll. Numerikus adatok :  45°, LaTex syntax error
45°, LaTex syntax error\setbox0\hbox{$m=4 \,\mathrm{kg}$}%
\message{//depth:\the\dp0//}% \box0%
,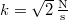 ,
, 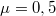 ,
, 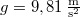 .
.
- a) Mekkora a test gyorsulása a
 időpontban?
időpontban?
- b) Add meg a test gyorsulását az idő függvényében! Mennyi idő telik el, míg a testre ható erők kiegyenlítik egymást?
- c) Mikor áll meg a test?
- d) Mekkora és milyen irányú a test gyorsulása a megállás pillanatában?
- e) Ha a lejtőt
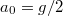 gyorsulással megtolnánk, mekkora lenne a test gyorsulása a
gyorsulással megtolnánk, mekkora lenne a test gyorsulása a  időpontban?
időpontban?
- a) Mekkora a test gyorsulása a
Megoldás
- a-b) Egy általános időpillanatban a testre ható erőket az ÁBRÁn ábrázoltuk. A gravitációs erőt érdemes felbontani egy lejtőre merőleges
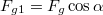 és egy a lejtővel párhuzamos
és egy a lejtővel párhuzamos 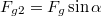 komponensre.
komponensre.
- a-b) Egy általános időpillanatban a testre ható erőket az ÁBRÁn ábrázoltuk. A gravitációs erőt érdemes felbontani egy lejtőre merőleges
ÁBRA
A lejtőre merőleges irányban nem történik mozgás, ezért![\[N=F_{g1}\,.\]](/images/math/1/f/0/1f04cdff3fa3b9ef4f8edfb3e5bf538b.png)
![\[ma(t)=F_{g2}-F(t)-S\,,\]](/images/math/6/3/7/637e11b93c4d6158bdb506e7e765d3a0.png)
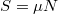 .
. ![\[ma(t)=mg\left(\sin\alpha - \mu\cos\alpha\right)-kt\]](/images/math/8/0/5/805fac3d4fb483ef0a5d0c2a00ada805.png)
 időpillanatban
időpillanatban 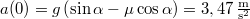 .
. Amikor a testre ható erők kiegyenlítik egymást, akkor a gyorsulás zérus. Ez abban a
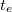 időpontban történik meg, amikor
időpontban történik meg, amikor 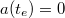 . Ebből
. Ebből ![\[t_{e}=\frac{mg}{k}\left(\sin\alpha - \mu\cos\alpha\right)=9,81\,\mathrm{s}\,.\]](/images/math/2/1/3/2132fec809119a28ee332507f2090048.png)
- c) A sebesség az idő függvényében az alábbiak szerint számolható ki. A kezdeti sebesség 0, így
![\[v(t)=v(0)+\int_{0}^{t}a(t')dt'\]](/images/math/b/6/2/b626776db780679c5049b4960bd1026b.png) A test abban a
A test abban a![\[v(t)=gt\left(\sin\alpha - \mu\cos\alpha\right)-\frac{k}{2m}t^{2}\,.\]](/images/math/1/f/e/1fe6aa55515b18e46e93e614d789f20d.png)
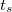 időpillanatban áll meg, amikor
időpillanatban áll meg, amikor 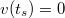 . Ebből az egyenletből a
. Ebből az egyenletből a 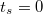 is adódik természetesen, hiszen a kezdeti időpillanatban is
is adódik természetesen, hiszen a kezdeti időpillanatban is  volt a sebesség, de fizikailag most az egyenlet másik megoldása érdekes.
volt a sebesség, de fizikailag most az egyenlet másik megoldása érdekes. ![\[t_{s}=\frac{2mg}{k}\left(\sin\alpha - \mu\cos\alpha\right)=19,62\,\mathrm{s}\,.\]](/images/math/f/6/c/f6ccee1742b4302f089e1fbd28ecd08b.png)
- d) A megállás pillanatában a gyorsulás éppen
![\[a(t_{s})=-g\left(\sin\alpha - \mu\cos\alpha\right)=-3,47\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/0/9/9/0992c32381d35712ab817f9322674423.png)
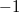 -szerese a kezdeti gyorsulásnak.
-szerese a kezdeti gyorsulásnak.
- e) Ha az ÁBRA szerinti elrendezésben megtoljuk a lejtőt, akkor a lejtőz rögzített rendszerben egy tehetetlenségi erőt kell figyelembe vennünk. Az ÁBRÁn a kezdeti időpillanatban ható erőket vázoltuk fel. A gravitációs erő mellett a tehetetlenségi erőt is érdemes felbontani lejtővel párhuzamos és arra merőleges komponensre.
- c) A sebesség az idő függvényében az alábbiak szerint számolható ki.
ÁBRA
A mozgásegyenlet a lejtőre merőleges irányban az erők kiegyenlítik egymást.![\[N=F_{g}\cos\alpha-F_{t}\sin\alpha=mg\left(\cos\alpha-\frac{\sin\alpha}{2}\right)\,.\]](/images/math/5/f/0/5f0b60e30c19175ff418211488b3a576.png)
![\[ma'(0)=F_{g}\sin\alpha-\mu N+F_{t}\cos\alpha=mg\left(\sin\alpha-\mu\left(\cos\alpha-\frac{\sin\alpha}{2}\right)+\frac{\cos\alpha}{2} \right)\]](/images/math/6/b/7/6b7c4bb629db0c255821708a2a270885.png)
![\[a'(0)=g\left(\sin\alpha-\mu\left(\cos\alpha-\frac{\sin\alpha}{2}\right)+\frac{\cos\alpha}{2} \right)=8,67\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/9/c/c/9cc138586598714042c70e8200422c1b.png)
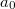 gyorsulást.
gyorsulást.