Erőtan I. - 2.4.1
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 12., 21:32-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Erőtan I. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
 tömegű golyóból és
tömegű golyóból és  hosszúságú, nyújthatatlan fonálból álló ingát a függőlegestől
hosszúságú, nyújthatatlan fonálból álló ingát a függőlegestől 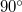 -kal kitérítünk, majd elengedünk. Mekkora erő feszíti a fonalat a golyó pályájának legalsó pontján való áthaladáskor? (A fonál tömege és a közegelenállás elhanyagolható.)
-kal kitérítünk, majd elengedünk. Mekkora erő feszíti a fonalat a golyó pályájának legalsó pontján való áthaladáskor? (A fonál tömege és a közegelenállás elhanyagolható.)
Megoldás
- A kezdeti pozícióban a golyó helyzeti energiája a legalsó ponthoz viszonyítva
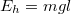 . Ezaz energia alakul át mozgási energiává a legalsó pontig történő mozgás során. A legalsó pontban a testre ható erőket az ÁBRÁn ábrázoltuk.
. Ezaz energia alakul át mozgási energiává a legalsó pontig történő mozgás során. A legalsó pontban a testre ható erőket az ÁBRÁn ábrázoltuk.![\[\frac{1}{2}mv^{2}=mgl\qquad\Rightarrow\qquad v=\sqrt{2gl}\]](/images/math/6/b/1/6b1944f53bcdb7d18070ad57acc8dc41.png)
- A kezdeti pozícióban a golyó helyzeti energiája a legalsó ponthoz viszonyítva
ÁBRA
Az eredő erőnek éppen a centripetális erőnek kell lennie, azaz![\[K-mg=m\frac{v^{2}}{l}\qquad\Rightarrow\qquad K=3mg\]](/images/math/2/8/3/283b7b007afc259dd4da216be0cd48bd.png)