Integrálás - Tömegközéppont számítás

Feladat

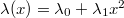1. Egy $\setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú rúd az $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ tengelyen fekszik, lineáris sűrűsége $\setbox0\hbox{$\lambda(x)=\lambda_{0}+\lambda_{1}x^{2}$}% \message{//depth:\the\dp0//}% \box0%$, és az origóban van a kisebb sűrűségű vége. (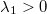$\setbox0\hbox{$\lambda_1>0$}% \message{//depth:\the\dp0//}% \box0%$) Hol van a rúd tömegközéppontja?

Megoldás

Mivel a lineráis sűrűség

$\[\lambda(x)=\frac{dm}{dx},\]$

így a számításhoz szükséges tömegelemek

$\[dm=\lambda(x)dx\]$

szerint írhatók fel. Először meg kell határozzuk a rúd össztömegét:

$\[m=\int dm\]$

szimbolikus integrált konkrétan valamelyik koordináta szerint kell felírni. Esetünkben ez egyszerűen az origótól mért $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ távolság, így az integrálás határai is egyszerűen megadhatók:

$\[m=\int_{0}^{d}\lambda(x)dx=\lambda_{0}d+\frac{\lambda_{1}d^{3}}{3}\]$

Felhasználva a tömegközéppont definícióját:

$\[mx_{\rm{TKP}}=\int x dm=\int_{0}^{d}x\lambda(x)dx=\int_{0}^{d}\left(\lambda_{0}x+\lambda_{1}x^{3}\right)dx=\frac{\lambda_{0}d^{2}}{2}+\frac{\lambda_{1}d^{4}}{4}\]$

Végül

$\[x_{\rm{TKP}}=\frac{\frac{\lambda_{0}d^{2}}{2}+\frac{\lambda_{1}d^{4}}{4}}{\lambda_{0}d+\frac{\lambda_{1}d^{3}}{3}}=\frac{\frac{\lambda_{0}d}{2}+\frac{\lambda_{1}d^{3}}{4}}{\lambda_{0}+\frac{\lambda_{1}d^{2}}{3}}\]$