Integrálás
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- Határozzuk meg az alábbi integrálokat!
- a)
![\[\int \left(3+4x+5x^{2}\right)dx\]](/images/math/4/b/2/4b2db38419b9f18cd58c88b080ab5dc1.png)
- b)
![\[\int_{-1}^{2}\left(x^{2}-\sin(5x)\right)dx\]](/images/math/2/6/0/2600c8c15e99e8308ee54fff0df29d0c.png)
- c)
![\[\int_{0}^{\pi}\sin^{2}x\,dx\]](/images/math/4/8/b/48b05376492ca302010168d09383a173.png)
- d)
![\[\int_{0}^{\pi}\cos^{2}x\,dx\]](/images/math/9/8/d/98dc32b7de1d0b2f040ea4af278e614d.png)
- e)
![\[\int\sqrt{3x+2}dx\]](/images/math/4/8/3/483106f173cac054e038addbc0b6af43.png)
- f)
![\[\int\frac{1}{2x}dx\]](/images/math/1/6/b/16b1a9170bf5c75ce98e459e167fcaaa.png)
- a)
- Határozzuk meg az
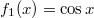 és az
és az 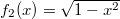 függvények által közrefogott területet a [-1,1] intervallumon!
függvények által közrefogott területet a [-1,1] intervallumon!
- * Határozzuk meg az alábbi integrálokat parciális integrálással!
- a)
![\[\int x\cos x \,dx\]](/images/math/2/e/1/2e1c4c5b5750faf60873240307a73b73.png)
- b)
![\[I=\int x^{2}e^{2x}dx\]](/images/math/1/2/8/128ae8d82a57ba5def5bef0294ca766d.png)
- c)
![\[I=\int e^{x}\sin x\,dx\]](/images/math/d/0/a/d0a9fea2785d66530873a5bb106678f4.png)
- a)
- * Határozzuk meg az alábbi integrálokat lehetőség szerint többféle módszerrel!
- a)
![\[\int e^{x}\mbox{sh} x\,dx\]](/images/math/c/8/5/c85ec32a9805d564de6b373645ecf759.png)
- b)
![\[\int\frac{1}{x^{2}+3}dx\]](/images/math/1/6/2/1622a50694d6aad64f076ecc09655c73.png)
- c)
![\[\int_{0}^{\pi}\sin^{3}x\,dx\]](/images/math/c/d/b/cdb2462bda9b53c47163fb33bde41542.png)
- d)
![\[\int\frac{\ln (2x)}{x}dx\]](/images/math/f/c/1/fc1e362c99c973096b02ed0a8aa0ee41.png)
- a)
- Egy
 hosszúságú rúd az
hosszúságú rúd az  tengelyen fekszik, lineáris sűrűsége
tengelyen fekszik, lineáris sűrűsége 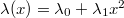 , és az origóban van a kisebb sűrűségű vége. (
, és az origóban van a kisebb sűrűségű vége. (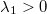 ) Hol van a rúd tömegközéppontja?
) Hol van a rúd tömegközéppontja?
- *
- a) Az alábbi határozott integrál a változó felső
 határ miatt annak függvénye: és egyenlő a
határ miatt annak függvénye: és egyenlő a![\[I(v)=\int_{0}^{v}\frac{1}{1-\alpha v'}dv'=t\]](/images/math/e/1/6/e1686d2cfc14de6e2c61b78269e28c51.png)
 időváltozóval. Határozzuk meg a
időváltozóval. Határozzuk meg a 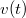 függvényt!
függvényt!
- b) Az alábbi határozott integrál a változó felső
 határ miatt annak függvénye: Határozzuk meg az
határ miatt annak függvénye: Határozzuk meg az![\[\alpha t= \int \limits _{\omega _0} ^\omega \frac{1}{\omega '^2} d\omega ' = I(\omega)\]](/images/math/a/8/6/a8630fdeb67f60cd300a3863e7f7a404.png)
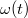 függvényt!
függvényt!
- c) Az alábbi határozott integrál a változó
 határ miatt annak függvénye: Határozzuk meg a
határ miatt annak függvénye: Határozzuk meg a![\[I (h) = \int \limits _{h_0} ^h \frac {1}{\sqrt{h '}} dh' = -c t \]](/images/math/f/0/0/f004e1aa9fd212e19ab2e889020a96b2.png)
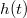 függvényt!
függvényt!
- a) Az alábbi határozott integrál a változó felső
- Egy parabola-antenna a nagy viharban leesett a háztetőről, és úgy ért a földre, hogy szimmetriatengelye éppen függőleges. A nagy esőben a tányér megtelt vízzel. Tudjuk, hogy a tányér mélysége középen
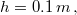 a tányér sugara pedig
a tányér sugara pedig 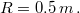
- a) Határozzuk meg, hogy mekkora térfogatú víz gyűlt össze a tányérban?
- b) Mekkora a tányér (belső) felülete?
![\[T=2sin(1) - \frac{\pi}2\]](/images/math/b/5/7/b57aa2a6824e5bc234ccbad7f717e79e.png)
![\[x\sin x+\cos x+C\]](/images/math/3/2/b/32b9057db69e58c0d4acd8bd4edd9368.png)
![\[e^{2x}\left(\frac{x^{2}}{2}-\frac{x}{2}+\frac{1}{4}\right)+C\]](/images/math/a/9/9/a99e105a028a643dc6cebe8480d2c8ca.png)
![\[\frac{e^{x}}{2}\left(\sin x-\cos x\right)+C\]](/images/math/4/a/8/4a84b6c718369247ec8fb9d5f801e469.png)
![\[\frac{e^{2x}}{4}-\frac{x}{2}+C\]](/images/math/1/1/2/112c9d9008ad8c9035e9f49bb0c0c1ed.png)
![\[\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C\]](/images/math/1/7/a/17ae43437200f976baf5faea2bdad36f.png)
![\[\frac43\]](/images/math/3/3/e/33ef116779b2381be20e42fb75bf5041.png)
![\[\frac{(\ln 2x)^2}2 +c\]](/images/math/c/7/3/c7317a97de0f65c4341a3c429c54104c.png)
![\[x_{\rm{TKP}}=\frac{\frac{\lambda_{0}d}{2}+\frac{\lambda_{1}d^{3}}{4}}{\lambda_{0}+\frac{\lambda_{1}d^{2}}{3}}\]](/images/math/b/5/a/b5aed4f9629168092e82aa7dfe7d9595.png)
![\[v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)\]](/images/math/9/0/6/9063f1fc9d57397f0628dc346ccee6cf.png)
![\[\omega (t) = \frac{ \omega _0}{1 - \omega _0 \alpha t}\]](/images/math/7/5/7/7572c6f68dccfaeadfa79c93fb8c0711.png)
![\[h(t) = h_0 + \frac {c^2 t^2 }{4} - c \sqrt { h_0 } \cdot t\]](/images/math/3/7/1/371d73f11c60e568794a87c605814941.png)
![\[V = \frac{R^2 h \pi}{2} = 0.0393 m^3 = 39.3 l \]](/images/math/4/2/a/42a02a7027c8cca7e84f8c47ce7151b0.png)
![\[ S = \frac{4 \pi R}{3 \sqrt{h}} \left[ \left( h + \frac{R^2}{4 h} \right)^{3/2} - \left( \frac{R^2}{4 h} \right)^{3/2} \right] = 0.816 m^2 \]](/images/math/b/2/b/b2b8365b623e9d4d50fe2d6cf26837bc.png)