Kinematika - Ferde hajítás

Feladat

1. Egy testet vízszintes terepen, a felszínnel 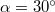$\setbox0\hbox{$\alpha = 30^{\circ}$}% \message{//depth:\the\dp0//}% \box0%$-os szöget bezáróan, 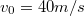$\setbox0\hbox{$v_0 = 40 m/s$}% \message{//depth:\the\dp0//}% \box0%$ sebességgel lövünk ki. Milyen messzire csapódik be a test a talajba a kilövés helyétől? Milyen magasra jut el mozgása során? Mekkora a pályája görbületi sugara a kilövés helyén, ill. a pálya tetőpontján?($\setbox0\hbox{$g=9,81\,\mathrm{\frac{m}{s^{2}}}$}% \message{//depth:\the\dp0//}% \box0%$)

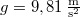Megoldás

1. A koordináta-rendszerünk origóját vegyük fel a kilövés helyén. A test gyorsulásvektora időben állandó,
   $\[\vec{a} = (0,-g) \; .\]$

Tudjuk, hogy 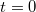$\setbox0\hbox{$t = 0$}% \message{//depth:\the\dp0//}% \box0%$ időpontban a test sebességvektora 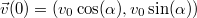$\setbox0\hbox{$\vec{v}(0) = (v_0 \cos(\alpha), v_0 \sin(\alpha))$}% \message{//depth:\the\dp0//}% \box0%$, ennek ismeretében a gyorsulás integrálásával, majd a kezdeti sebesség illesztésével megkapjuk a sebesség-idő függvényt:

$\[\vec{v}(t) = (v_0 \cos(\alpha), v_0 \sin(\alpha) - g t )\]$

.

Ismételt integrálással, kihasználva, hogy az origót a kilövés helyén vettük fel, a test helyvektora:

$\[\vec{r}(t) = (v_0 \cos(\alpha) t, v_0 \sin(\alpha) t - \frac{g}{2} t^2) \]$

Akkor csapódik a test a földbe, amikor 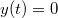$\setbox0\hbox{$y(t) = 0$}% \message{//depth:\the\dp0//}% \box0%$ lesz ismét:

$\[v_0 \sin(\alpha) t_{cs} - \frac{g}{2} t_{cs}^2 = 0 \]$

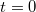Ebből a $\setbox0\hbox{$t = 0$}% \message{//depth:\the\dp0//}% \box0%$ megoldás a kilövés pillanatát jelzi. Nekünk a másik kell, ami

$\[t_{cs} = \frac{2 v_0 \sin(\alpha)}{g}\]$

A becsapódás távolságát úgy nyerjük, hogy ezt beírjuk az 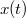$\setbox0\hbox{$x(t)$}% \message{//depth:\the\dp0//}% \box0%$ kifejezésbe:

$\[d = v_0 \cos(\alpha) t_{cs} = \frac{2 v_0^2 \sin(\alpha) \cos(\alpha)}{g}\]$

A maximális magasságot ott éri el a test, ahol 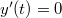$\setbox0\hbox{$y'(t) = 0$}% \message{//depth:\the\dp0//}% \box0%$, azaz

$\[v_0 \sin(\alpha) - g t_{max} = 0 \; ,\]$

amiből

$\[t_{max} = \frac{v_0 \sin(\alpha)}{g} \; .\]$

Beírva ezt az 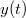$\setbox0\hbox{$y(t)$}% \message{//depth:\the\dp0//}% \box0%$ függvénybe nyerjük a maximális magasságot:

$\[h = y(t_{max}) = \frac{v_0^2 \sin^2(\alpha)}{2 g}\]$

A kilövési pontban a sebesség nagysága 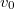$\setbox0\hbox{$v_0$}% \message{//depth:\the\dp0//}% \box0%$, a gyorsulásnak az erre merőleges komponense 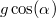$\setbox0\hbox{$g \cos(\alpha)$}% \message{//depth:\the\dp0//}% \box0%$, ebből a görbületi sugár:

$\[R_{start} = \frac{v_0^2}{g \cos(\alpha)}\]$

A tetőponton a sebesség nagysága 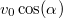$\setbox0\hbox{$v_0 \cos(\alpha)$}% \message{//depth:\the\dp0//}% \box0%$, a gyorsulás pedig éppen merőleges rá. Ezért a görbületi sugár:

$\[R_{fent} = \frac{v_0^2 \cos^2(\alpha)}{g}\]$