„Kinematika - 1.4.20” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Feladat) |
||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
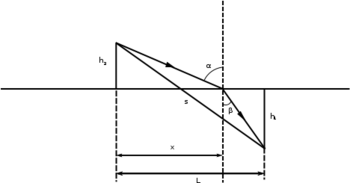
| − | </noinclude><wlatex># (1.4.20) Egy ember a tó partján sétálva a tóban egy fuldoklót vesz észre. A fuldokló a parttól $h_{1}$, az ember $h_{2}$ távolságban van. A fuldokló és a mentésére siető távolsága $s$. Milyen úton haladjon a mentésre siető ember, hogy a fuldoklót leghamarabb elérje, ha a parton futva $v_{2}$, a vízben úszva $v_{1}$ sebességgel tud haladni? | + | </noinclude><wlatex># (1.4.20) Egy ember a tó partján sétálva a tóban egy fuldoklót vesz észre. A fuldokló a parttól $h_{1}$, az ember $h_{2}$ távolságban van. A fuldokló és a mentésére siető távolsága $s$. Milyen úton haladjon a mentésre siető ember, hogy a fuldoklót leghamarabb elérje, ha a parton futva $v_{2}$, a vízben úszva $v_{1}$ sebességgel tud haladni? |
</wlatex><includeonly><wlatex></wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex></wlatex></includeonly><noinclude> | ||
A lap 2013. szeptember 25., 14:01-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (1.4.20) Egy ember a tó partján sétálva a tóban egy fuldoklót vesz észre. A fuldokló a parttól
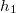, az ember 
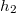távolságban van. A fuldokló és a mentésére siető távolsága 
. Milyen úton haladjon a mentésre siető ember, hogy a fuldoklót leghamarabb elérje, ha a parton futva 
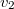, a vízben úszva 
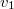sebességgel tud haladni?
Megoldás
- A távolságok rögzítettek, ezért az ábrán szereplő
távolság is rögzített. A mentésre indulónak azt kell eldöntenie, hogy milyen 
szög alatt kell a part felé indulnia, és milyen 
irányba ússzon. A mentés összes ideje az ábrán jelzett
távolság függvényében szerint írható. Az idő minimális, ha![\[T(x)=\frac{\sqrt{h_{2}^{2}+x^{2}}}{v_{2}}+\frac{\sqrt{h_{1}^{2}+(L-x)^{2}}}{v_{1}}\]](/images/math/b/f/d/bfd5d4c05b09de29878b121585040e24.png)
![\[\frac{dT}{dx}=0\]](/images/math/f/9/6/f96f186ac0c37cd905e7f27d3d8ce3df.png)
Az ábra alapján észrevehetjük, hogy![\[\frac{1}{v_{2}}\frac{x}{\sqrt{h_{2}^{2}+x^{2}}}-\frac{1}{v_{1}}\frac{L-x}{\sqrt{h_{2}^{2}+(L-x)^{2}}}=0\,.\]](/images/math/7/3/3/733741f9370e7f9dfc314e9baeefe8dd.png)
így a minimális időt az alábbi feltétel határozza meg.![\[\frac{x}{\sqrt{h_{2}^{2}+x^{2}}}=\sin\alpha\qquad\mbox{és}\qquad\frac{L-x}{\sqrt{h_{2}^{2}+(L-x)^{2}}}=\sin\beta\,,\]](/images/math/e/5/d/e5dc0a1603e3027346a319b1d2e403d2.png)
Az eredményben felismerhetjük a Snellius-Descartes törvényt. Az optikában a fény terjedésének leírásához általában is használható az úgynevezett Fermat-elv, amely variációs elvnek a mechanikai analógiája ez a feladat.![\[\frac{\sin\alpha}{\sin\beta}=\frac{v_{2}}{v_{1}}\]](/images/math/d/f/4/df43d74f3c20a4203f7a492138e4b27b.png)
- A távolságok rögzítettek, ezért az ábrán szereplő
