„Erőtan I. - 2.1.35” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Erőtan I. {{Kísérleti fizika gyakorlat | tárgynév …”) |
(→Megoldás) |
||
| (2 szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő: Bácsi Ádám]] | [[Kategória:Szerkesztő: Bácsi Ádám]] | ||
| − | [[Kategória:Erőtan I.]] | + | [[Kategória:Mechanika - Erőtan I.]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| − | | témakör = Erőtan I. | + | | témakör = Mechanika - Erőtan I. |
}} | }} | ||
== Feladat == | == Feladat == | ||
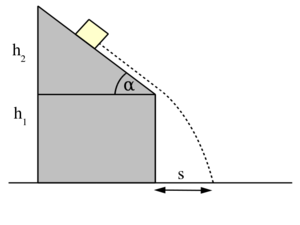
| − | </noinclude><wlatex># Vízszintes sík fölött $h_{1}$ magasságban $\alpha$ hajlásszögű, $h_{2}$ magasságú lejtőt helyezünk el. Ennek tetejéről test csúszik le, mely a vízszintesen mérve a lejtő csúcsától $s$ távolságban csapódik le. (2.1.35.ábra) Mennyi a lejtő és a test között a súrlódási együttható? ($\alpha=45^\circ$, $h_{1}=24\,\mathrm{m}$, $h_{2}=10\,\mathrm{m}$, $s=12\,\mathrm{m}$.) | + | </noinclude><wlatex># (2.1.35) Vízszintes sík fölött $h_{1}$ magasságban $\alpha$ hajlásszögű, $h_{2}$ magasságú lejtőt helyezünk el. Ennek tetejéről test csúszik le, mely a vízszintesen mérve a lejtő csúcsától $s$ távolságban csapódik le. (2.1.35.ábra) Mennyi a lejtő és a test között a súrlódási együttható? ($\alpha=45^\circ$, $h_{1}=24\,\mathrm{m}$, $h_{2}=10\,\mathrm{m}$, $s=12\,\mathrm{m}$.) [[Kép:Kfgy1_2.1.35.svg|none|300px]]</wlatex><includeonly><wlatex>{{Végeredmény|content= $\mu=0,4$ }}</wlatex></includeonly><noinclude> |
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content= $\mu=0,4$ }}</wlatex></includeonly><noinclude> | + | |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: A lejtőn a test gyorsulása $$a=g(\sin\alpha-\mu\cos\alpha)\,.$$ A lejtő alján a sebessége $$v=\sqrt{2a\frac{h_{2}}{\sin\alpha}}=\sqrt{2gh_{2}(1-\mu\,\mbox{ctg}\,\alpha)}\,,$$ mert a lejtőn megteendő út éppen $h_{2}/\sin\alpha$. A test a lejtőt elhagyva ferde hajításnak megfelelő mozgást végez. A sebesség $x$ komponense végig $v_{x}=v\cos\alpha$, tehát az esés ideje $$T=\frac{s}{v_{x}}=\frac{s}{v\cos\alpha}\,.$$ Ennyi idő alatt esett le a test a földig, vagyis $$h_{1}=Tv\sin\alpha+\frac{g}{2}T^{2}=s\,\mbox{tg}\,\alpha+\frac{gs^{2}}{2v^{2}\cos^{2}\alpha}\,.$$ Behelyettesítve a sebességre kapott formulával az $$h_{1}-s\,\mbox{tg}\,\alpha=\frac{s^{2}}{4h_{2}(1-\mu\,\mbox{ctg}\,\alpha)\cos^{2}\alpha}$$ egyenletre jutunk, amelyben minden adat ismert a súrlódási tényezőt kivéve. Azt kifejezve $$\mu=\,\mbox{tg}\,\left[1-\frac{s^{2}}{4h_{2}(h_{1}-s\,\mbox{tg}\,\alpha)\cos^{2}\alpha}\right]=0,4\,.$$ | + | <wlatex>#: A lejtőn a test gyorsulása $$a=g(\sin\alpha-\mu\cos\alpha)\,.$$ A lejtő alján a sebessége $$v=\sqrt{2a\frac{h_{2}}{\sin\alpha}}=\sqrt{2gh_{2}(1-\mu\,\mbox{ctg}\,\alpha)}\,,$$ mert a lejtőn megteendő út éppen $h_{2}/\sin\alpha$. A test a lejtőt elhagyva ferde hajításnak megfelelő mozgást végez. A sebesség $x$ komponense végig $v_{x}=v\cos\alpha$, tehát az esés ideje $$T=\frac{s}{v_{x}}=\frac{s}{v\cos\alpha}\,.$$ Ennyi idő alatt esett le a test a földig, vagyis $$h_{1}=Tv\sin\alpha+\frac{g}{2}T^{2}=s\,\mbox{tg}\,\alpha+\frac{gs^{2}}{2v^{2}\cos^{2}\alpha}\,.$$ Behelyettesítve a sebességre kapott formulával az $$h_{1}-s\,\mbox{tg}\,\alpha=\frac{s^{2}}{4h_{2}(1-\mu\,\mbox{ctg}\,\alpha)\cos^{2}\alpha}$$ egyenletre jutunk, amelyben minden adat ismert a súrlódási tényezőt kivéve. Azt kifejezve $$\mu=\,\mbox{tg}\alpha\,\left[1-\frac{s^{2}}{4h_{2}(h_{1}-s\,\mbox{tg}\,\alpha)\cos^{2}\alpha}\right]=0,4\,.$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. október 1., 15:08-kori változata
Feladat
- (2.1.35) Vízszintes sík fölött
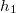magasságban 
hajlásszögű,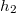 
magasságú lejtőt helyezünk el. Ennek tetejéről test csúszik le, mely a vízszintesen mérve a lejtő csúcsától 
távolságban csapódik le. (2.1.35.ábra) Mennyi a lejtő és a test között a súrlódási együttható? (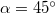
, 
, 
, 
.) 
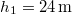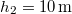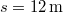Megoldás
- A lejtőn a test gyorsulása A lejtő alján a sebessége
![\[a=g(\sin\alpha-\mu\cos\alpha)\,.\]](/images/math/2/d/0/2d0e07ee5e49b4a9365607c8b5405a1d.png)
mert a lejtőn megteendő út éppen![\[v=\sqrt{2a\frac{h_{2}}{\sin\alpha}}=\sqrt{2gh_{2}(1-\mu\,\mbox{ctg}\,\alpha)}\,,\]](/images/math/2/3/4/2343a818758898b568ce36766e94c3d5.png)
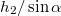. A test a lejtőt elhagyva ferde hajításnak megfelelő mozgást végez. A sebesség 
komponense végig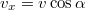 
, tehát az esés ideje Ennyi idő alatt esett le a test a földig, vagyis![\[T=\frac{s}{v_{x}}=\frac{s}{v\cos\alpha}\,.\]](/images/math/8/d/d/8ddf1403afeb8b5ce88fb862a580abaa.png)
Behelyettesítve a sebességre kapott formulával az![\[h_{1}=Tv\sin\alpha+\frac{g}{2}T^{2}=s\,\mbox{tg}\,\alpha+\frac{gs^{2}}{2v^{2}\cos^{2}\alpha}\,.\]](/images/math/0/7/6/0767260c66b6313abad0b1e13fdaff49.png)
egyenletre jutunk, amelyben minden adat ismert a súrlódási tényezőt kivéve. Azt kifejezve![\[h_{1}-s\,\mbox{tg}\,\alpha=\frac{s^{2}}{4h_{2}(1-\mu\,\mbox{ctg}\,\alpha)\cos^{2}\alpha}\]](/images/math/3/d/6/3d6fbd7dc959a780d480befc55ebe62c.png)
![\[\mu=\,\mbox{tg}\alpha\,\left[1-\frac{s^{2}}{4h_{2}(h_{1}-s\,\mbox{tg}\,\alpha)\cos^{2}\alpha}\right]=0,4\,.\]](/images/math/7/7/5/775cac297f597cc6cf1ced925f9d5491.png)
- A lejtőn a test gyorsulása
