„Kinematika - 1.4.23” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| (2 szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
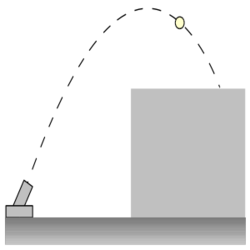
| − | </noinclude><wlatex># (1.4.23) Egy aknavetővel a völgyből $h$ magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége $v_{0}$. [[Kép:Kfgy1_03_1_4_23.svg|none|250px]] | + | </noinclude><wlatex># (*1.4.23) Egy aknavetővel a völgyből $h$ magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége $v_{0}$. [[Kép:Kfgy1_03_1_4_23.svg|none|250px]] |
</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}$$ $$D=\frac{v_{0}^{2}}{g}-2h\,.$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$\varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}$$ $$D=\frac{v_{0}^{2}}{g}-2h\,.$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
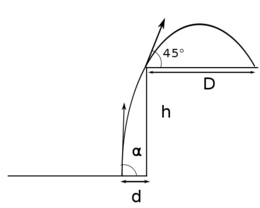
| − | <wlatex>#: A lövedék pályája egy parabolát ír le. Olyan pálya lehet az optimális, amelyik éppen érinti a fennsík peremét. Ez az állítás indirekt módon látható be. Képzeljünk el egy olyan pályát, amely a fennsík pereme felett halad el. Ennél azonban biztosan távolabbra tudunk lőni, ha az aknavetőt közelebb toljuk és ugyanabban a szögben lövünk. Természetesen az olyan pályák, melyek a fennsík pereme alatt haladnának, teljes mértékben érdektelenek. <br><br> Tehát olyan pályákat vizsgálunk, amelyek éppen a fennsík peremét érintik. Amikor a lövedék eléri a peremet, akkor a sebességének nagysága a kilövés szögétől és a kilövés helyétől függetlenül $v_{1}$ lesz, melyet az alábbi energetikai megfontolásból számolhatunk ki. $$\frac{1}{2}mv_{0}^{2}=mgh+\frac{1}{2}mv_{1}^{2}\qquad\Rightarrow\qquad v_{1}=v_{0}\sqrt{1-\frac{2hg}{v_{0}^{2}}}$$ Most vizsgáljuk meg, hogy milyen szögűnek kell lennie a $v_{1}$ sebességnek ahhoz, hogy a maximális legyen a felszínen megtett út. Ha a vízszintessel bezárt szög $\alpha$, akkor a sebbeség különböző irányú komponenseinek nagysága $$v_{1x}=v_{1}\cos\alpha\qquad\qquad v_{1y}=v_{1}\sin\alpha\,.$$ A a felszínen a becsapódásig $t_{1}(\alpha)=2v_{1y}/g$ idő telik el. Ezalatt a lövedék vízszintes irányba $$x_{1}(\alpha)=v_{1x}t_{1}=\frac{ | + | <wlatex>#: A lövedék pályája egy parabolát ír le. Olyan pálya lehet az optimális, amelyik éppen érinti a fennsík peremét. Ez az állítás indirekt módon látható be. Képzeljünk el egy olyan pályát, amely a fennsík pereme felett halad el. Ennél azonban biztosan távolabbra tudunk lőni, ha az aknavetőt közelebb toljuk és ugyanabban a szögben lövünk. Természetesen az olyan pályák, melyek a fennsík pereme alatt haladnának, teljes mértékben érdektelenek. <br><br> Tehát olyan pályákat vizsgálunk, amelyek éppen a fennsík peremét érintik. Amikor a lövedék eléri a peremet, akkor a sebességének nagysága a kilövés szögétől és a kilövés helyétől függetlenül $v_{1}$ lesz, melyet az alábbi energetikai megfontolásból számolhatunk ki. $$\frac{1}{2}mv_{0}^{2}=mgh+\frac{1}{2}mv_{1}^{2}\qquad\Rightarrow\qquad v_{1}=v_{0}\sqrt{1-\frac{2hg}{v_{0}^{2}}}$$ Most vizsgáljuk meg, hogy milyen szögűnek kell lennie a $v_{1}$ sebességnek ahhoz, hogy a maximális legyen a felszínen megtett út. Ha a vízszintessel bezárt szög $\alpha$, akkor a sebbeség különböző irányú komponenseinek nagysága $$v_{1x}=v_{1}\cos\alpha\qquad\qquad v_{1y}=v_{1}\sin\alpha\,.$$ A a felszínen a becsapódásig $t_{1}(\alpha)=2v_{1y}/g$ idő telik el. Ezalatt a lövedék vízszintes irányba $$x_{1}(\alpha)=v_{1x}t_{1}=\frac{2v_{1}^{2}}{g}\sin\alpha\cos\alpha$$ utat tesz meg. A kifejezés maximális, ha $\alpha=45^{\circ}$ és ekkor a megtett út $D=x_{1\mathrm{max}}=v_{1}^{2}/g$. A kérdés tehát az, hogy honnan és milyen szög alatt kell lőni ahhoz, hogy a pálya a fennsík peremét érintse, és ebben a pillanatban a vízszintessel $45$ fokos szöget zár be a sebesség. [[Kép:1.4.23.M.svg|none|260px]] Kihasználhatjuk azt a tényt, hogy a mozgás során az $x$ irányú sebesség végig változatlan. Amikor a lövedék a fennsík pereménél van, akkor $v_{x}=v_{1}\sin 45^\circ=v_{1}/\sqrt{2}$. Ennek azonban meg kell egyeznie a kilövés pillanatában mérhető $x$ irányú sebességgel $v_{x}=v_{0}\cos\varphi$. Ezek alapján ki lehet számolni azt a szöget, amely alatt a lövedéket ki kell lőni. $$\frac{v_{1}}{\sqrt{2}}=v_{0}\cos\varphi$$$$\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}=\cos\varphi\qquad\Rightarrow\qquad \varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}$$ <br><br> Ahhoz, hogy meghatározzuk a kilövés helyét, ki kell számolnunk, hogy mennyi időbe ($\Delta t$) telik, amíg a lövedék a kilövés után eléri a fennsík peremét. Ehhez meg kell oldanunk a $$h=v_{0}\sin\varphi\Delta t-\frac{g}{2}\Delta t^{2}$$ másodfokú egyenletet. A két megoldás közül az egyik (kisebb) azt az időtartamot adja meg, ami alatt a lövedék eléri a fennsík peremét. A másik (nagyobb) megoldás azt az időpontot határozza meg, amikor a lövedék $D$ távolságban becsapódik. Nekünk most az előbbire van szükségünk, mert ez alapján az aknavető távolsága a fennsík szélétől $$d=\frac{v_{1}}{\sqrt{2}}\Delta t_{1}=\frac{v_{1}}{2g}\left[\sqrt{v_{0}^{2}+2gh}-v_{1}\right]$$ <br> Összefoglalva az eredményeket: <br> Ahhoz, hogy a lövedék a lehető legmesszebb csapódjon be a fennsíkon, az aknavetőt a fennsík szélétől $$d=\frac{\sqrt{v_{0}^{2}-2hg}}{2g}\left[\sqrt{v_{0}^{2}+2gh}-\sqrt{v_{0}^{2}-2hg}\right]$$ távolságban kell elhelyezni és a lövedéket $$\varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}$$ szögben kell kilőni. A fennsíkon megtett út ebben az esetben $$D=\frac{v_{0}^{2}}{g}-2h\,.$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 9., 16:22-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*1.4.23) Egy aknavetővel a völgyből
 magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége
magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége 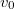 .
.
Megoldás
- A lövedék pályája egy parabolát ír le. Olyan pálya lehet az optimális, amelyik éppen érinti a fennsík peremét. Ez az állítás indirekt módon látható be. Képzeljünk el egy olyan pályát, amely a fennsík pereme felett halad el. Ennél azonban biztosan távolabbra tudunk lőni, ha az aknavetőt közelebb toljuk és ugyanabban a szögben lövünk. Természetesen az olyan pályák, melyek a fennsík pereme alatt haladnának, teljes mértékben érdektelenek.
Tehát olyan pályákat vizsgálunk, amelyek éppen a fennsík peremét érintik. Amikor a lövedék eléri a peremet, akkor a sebességének nagysága a kilövés szögétől és a kilövés helyétől függetlenül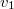 lesz, melyet az alábbi energetikai megfontolásból számolhatunk ki. Most vizsgáljuk meg, hogy milyen szögűnek kell lennie a
lesz, melyet az alábbi energetikai megfontolásból számolhatunk ki. Most vizsgáljuk meg, hogy milyen szögűnek kell lennie a![\[\frac{1}{2}mv_{0}^{2}=mgh+\frac{1}{2}mv_{1}^{2}\qquad\Rightarrow\qquad v_{1}=v_{0}\sqrt{1-\frac{2hg}{v_{0}^{2}}}\]](/images/math/1/d/5/1d5afb4c6082f9f3d5710083c41c87f0.png)
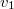 sebességnek ahhoz, hogy a maximális legyen a felszínen megtett út. Ha a vízszintessel bezárt szög
sebességnek ahhoz, hogy a maximális legyen a felszínen megtett út. Ha a vízszintessel bezárt szög  , akkor a sebbeség különböző irányú komponenseinek nagysága A a felszínen a becsapódásig
, akkor a sebbeség különböző irányú komponenseinek nagysága A a felszínen a becsapódásig![\[v_{1x}=v_{1}\cos\alpha\qquad\qquad v_{1y}=v_{1}\sin\alpha\,.\]](/images/math/5/b/9/5b94075e77ed2161350a7e5fa7a2eebf.png)
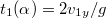 idő telik el. Ezalatt a lövedék vízszintes irányba utat tesz meg. A kifejezés maximális, ha
idő telik el. Ezalatt a lövedék vízszintes irányba utat tesz meg. A kifejezés maximális, ha![\[x_{1}(\alpha)=v_{1x}t_{1}=\frac{2v_{1}^{2}}{g}\sin\alpha\cos\alpha\]](/images/math/9/4/4/9449b0a5ea142bd92dcf76cb66e6c95a.png)
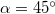 és ekkor a megtett út
és ekkor a megtett út 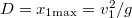 . A kérdés tehát az, hogy honnan és milyen szög alatt kell lőni ahhoz, hogy a pálya a fennsík peremét érintse, és ebben a pillanatban a vízszintessel
. A kérdés tehát az, hogy honnan és milyen szög alatt kell lőni ahhoz, hogy a pálya a fennsík peremét érintse, és ebben a pillanatban a vízszintessel 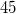 fokos szöget zár be a sebesség. Kihasználhatjuk azt a tényt, hogy a mozgás során az
fokos szöget zár be a sebesség. Kihasználhatjuk azt a tényt, hogy a mozgás során az  irányú sebesség végig változatlan. Amikor a lövedék a fennsík pereménél van, akkor
irányú sebesség végig változatlan. Amikor a lövedék a fennsík pereménél van, akkor 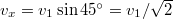 . Ennek azonban meg kell egyeznie a kilövés pillanatában mérhető
. Ennek azonban meg kell egyeznie a kilövés pillanatában mérhető  irányú sebességgel
irányú sebességgel 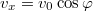 . Ezek alapján ki lehet számolni azt a szöget, amely alatt a lövedéket ki kell lőni.
. Ezek alapján ki lehet számolni azt a szöget, amely alatt a lövedéket ki kell lőni. ![\[\frac{v_{1}}{\sqrt{2}}=v_{0}\cos\varphi\]](/images/math/8/5/b/85b663c95f7131cba71713eeb76293f9.png)
![\[\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}=\cos\varphi\qquad\Rightarrow\qquad \varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}\]](/images/math/f/7/2/f72cc09b2bc1c2d7f8473173940020a9.png)
Ahhoz, hogy meghatározzuk a kilövés helyét, ki kell számolnunk, hogy mennyi időbe ( ) telik, amíg a lövedék a kilövés után eléri a fennsík peremét. Ehhez meg kell oldanunk a másodfokú egyenletet. A két megoldás közül az egyik (kisebb) azt az időtartamot adja meg, ami alatt a lövedék eléri a fennsík peremét. A másik (nagyobb) megoldás azt az időpontot határozza meg, amikor a lövedék
) telik, amíg a lövedék a kilövés után eléri a fennsík peremét. Ehhez meg kell oldanunk a másodfokú egyenletet. A két megoldás közül az egyik (kisebb) azt az időtartamot adja meg, ami alatt a lövedék eléri a fennsík peremét. A másik (nagyobb) megoldás azt az időpontot határozza meg, amikor a lövedék![\[h=v_{0}\sin\varphi\Delta t-\frac{g}{2}\Delta t^{2}\]](/images/math/c/3/d/c3df5756e396598319e390b3df23bccd.png)
 távolságban becsapódik. Nekünk most az előbbire van szükségünk, mert ez alapján az aknavető távolsága a fennsík szélétől
távolságban becsapódik. Nekünk most az előbbire van szükségünk, mert ez alapján az aknavető távolsága a fennsík szélétől ![\[d=\frac{v_{1}}{\sqrt{2}}\Delta t_{1}=\frac{v_{1}}{2g}\left[\sqrt{v_{0}^{2}+2gh}-v_{1}\right]\]](/images/math/e/2/3/e23f62b160605bd4b25ec1fc84773fac.png)
Összefoglalva az eredményeket:
Ahhoz, hogy a lövedék a lehető legmesszebb csapódjon be a fennsíkon, az aknavetőt a fennsík szélétőltávolságban kell elhelyezni és a lövedéket![\[d=\frac{\sqrt{v_{0}^{2}-2hg}}{2g}\left[\sqrt{v_{0}^{2}+2gh}-\sqrt{v_{0}^{2}-2hg}\right]\]](/images/math/e/3/f/e3f12fd85ac30eb0b3611a8680b4c3b8.png) szögben kell kilőni. A fennsíkon megtett út ebben az esetben
szögben kell kilőni. A fennsíkon megtett út ebben az esetben![\[\varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}\]](/images/math/c/b/3/cb3a2e723a373e2c2b55afd5e5011270.png)
![\[D=\frac{v_{0}^{2}}{g}-2h\,.\]](/images/math/6/4/9/64909bf4299497b17ab066ed1374ca88.png)
- A lövedék pályája egy parabolát ír le. Olyan pálya lehet az optimális, amelyik éppen érinti a fennsík peremét. Ez az állítás indirekt módon látható be. Képzeljünk el egy olyan pályát, amely a fennsík pereme felett halad el. Ennél azonban biztosan távolabbra tudunk lőni, ha az aknavetőt közelebb toljuk és ugyanabban a szögben lövünk. Természetesen az olyan pályák, melyek a fennsík pereme alatt haladnának, teljes mértékben érdektelenek.