„Erőtan I. - 2.1.26” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő: Bácsi Ádám]] | [[Kategória:Szerkesztő: Bácsi Ádám]] | ||
| − | [[Kategória:Erőtan I.]] | + | [[Kategória:Mechanika - Erőtan I.]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Sima, vízszintes síkon levő kis méretű testre $F(t)=kt$ törvény szerint változó erő hat úgy, hogy iránya a vízszintessel $\alpha$ szöget zár be. A test és a sík közti súrlódástól eltekintünk. Határozza meg | + | </noinclude><wlatex># (*2.1.26) Sima, vízszintes síkon levő kis méretű testre $F(t)=kt$ törvény szerint változó erő hat úgy, hogy iránya a vízszintessel $\alpha$ szöget zár be. A test és a sík közti súrlódástól eltekintünk. Határozza meg |
#: a) a test sebességét abban a pillanatban, amikor a test kezd felemelkedni, | #: a) a test sebességét abban a pillanatban, amikor a test kezd felemelkedni, | ||
#: b) a felemelkedés kezdetéig befutott utat! ($v(t=0)=0$ és $x(t=0)=0$) | #: b) a felemelkedés kezdetéig befutott utat! ($v(t=0)=0$ és $x(t=0)=0$) | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content= Határozzuk meg először azt az időpontot, amikor a test felemelkedik! A gyorsulás integrálásával határozzuk meg a sebesség, majd még egyszer integrálva a test helyzetének időfüggését}}{{Végeredmény|content= a) $$v(t_{e})=\frac{mg^{2}\cos\alpha}{2k\sin^{2}\alpha}$$ <br> b) $$x(t_{e})=\frac{m^{2}g^{3}\cos\alpha}{ | + | </wlatex><includeonly><wlatex>{{Útmutatás|content= Határozzuk meg először azt az időpontot, amikor a test felemelkedik! A gyorsulás integrálásával határozzuk meg a sebesség, majd még egyszer integrálva a test helyzetének időfüggését}}{{Végeredmény|content= a) $$v(t_{e})=\frac{mg^{2}\cos\alpha}{2k\sin^{2}\alpha}$$ <br> b) $$x(t_{e})=\frac{m^{2}g^{3}\cos\alpha}{6k^{2}\sin^{3}\alpha}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>#: a) A testre az $F(t)$ erőn kívül a függőleges irányú gravitációs és nyomóerők hatnak. Az általunk kifejtett erőt érdemes felbontani egy $F_{x}(t)=F(t)\cos\alpha$ nagyságú vízszintes és egy $F_{y}(t)=F(t)\sin\alpha$ nagyságú függőleges komponensre. Amíg a test el nem emelkedik, addig a függőleges irányban az erők kiegyenlítik egymást. $$N=mg-kt\sin\alpha$$ Ez egészen addig a $t_{e}$ pillanatig tart, amíg a nyomórerő zérussá nem válik. Ezután már nem tud megtörténni az erők kiegyenlítődése, hiszen a nyomóerő nem lehet negatív. $$0=mg-kt_{e}\sin\alpha\qquad\Rightarrow\qquad t_{e}=\frac{mg}{k\sin\alpha}$$ A vízszintes irányú mozgásegyenlet: $$ma(t)=kt\cos\alpha$$ Ez alapján a sebesség az idő függvényében $$v(t)=v(0)+\int_{0}^{t}a(t')dt'=\frac{k\cos\alpha}{2m}t^{2}$$ A felemelkedés pillanatában tehát $$v(t_{e})=\frac{mg^{2}\cos\alpha}{2k\sin^{2}\alpha}\,.$$ | <wlatex>#: a) A testre az $F(t)$ erőn kívül a függőleges irányú gravitációs és nyomóerők hatnak. Az általunk kifejtett erőt érdemes felbontani egy $F_{x}(t)=F(t)\cos\alpha$ nagyságú vízszintes és egy $F_{y}(t)=F(t)\sin\alpha$ nagyságú függőleges komponensre. Amíg a test el nem emelkedik, addig a függőleges irányban az erők kiegyenlítik egymást. $$N=mg-kt\sin\alpha$$ Ez egészen addig a $t_{e}$ pillanatig tart, amíg a nyomórerő zérussá nem válik. Ezután már nem tud megtörténni az erők kiegyenlítődése, hiszen a nyomóerő nem lehet negatív. $$0=mg-kt_{e}\sin\alpha\qquad\Rightarrow\qquad t_{e}=\frac{mg}{k\sin\alpha}$$ A vízszintes irányú mozgásegyenlet: $$ma(t)=kt\cos\alpha$$ Ez alapján a sebesség az idő függvényében $$v(t)=v(0)+\int_{0}^{t}a(t')dt'=\frac{k\cos\alpha}{2m}t^{2}$$ A felemelkedés pillanatában tehát $$v(t_{e})=\frac{mg^{2}\cos\alpha}{2k\sin^{2}\alpha}\,.$$ | ||
| − | #: b) Az elmozdulás az idő függvényében az alábbiak szerint számolható ki. $$x(t)=x(0)+\int_{0}^{t}v(t')dt'=\frac{k\cos\alpha}{6m}t^{3}$$ Így a felemelkedésig megtett út $$x(t_{e})=\frac{m^{2}g^{3}\cos\alpha}{ | + | #: b) Az elmozdulás az idő függvényében az alábbiak szerint számolható ki. $$x(t)=x(0)+\int_{0}^{t}v(t')dt'=\frac{k\cos\alpha}{6m}t^{3}$$ Így a felemelkedésig megtett út $$x(t_{e})=\frac{m^{2}g^{3}\cos\alpha}{6k^{2}\sin^{3}\alpha}\,.$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 9., 16:23-kori változata
Feladat
- (*2.1.26) Sima, vízszintes síkon levő kis méretű testre
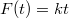törvény szerint változó erő hat úgy, hogy iránya a vízszintessel 
szöget zár be. A test és a sík közti súrlódástól eltekintünk. Határozza meg
- a) a test sebességét abban a pillanatban, amikor a test kezd felemelkedni,
- b) a felemelkedés kezdetéig befutott utat! (
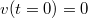és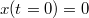 
)
Megoldás
- a) A testre az
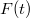erőn kívül a függőleges irányú gravitációs és nyomóerők hatnak. Az általunk kifejtett erőt érdemes felbontani egy 
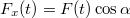nagyságú vízszintes és egy 
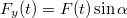nagyságú függőleges komponensre. Amíg a test el nem emelkedik, addig a függőleges irányban az erők kiegyenlítik egymást. Ez egészen addig a![\[N=mg-kt\sin\alpha\]](/images/math/4/8/6/486a1cd1101fdf23608a644820e93614.png)
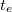pillanatig tart, amíg a nyomórerő zérussá nem válik. Ezután már nem tud megtörténni az erők kiegyenlítődése, hiszen a nyomóerő nem lehet negatív. A vízszintes irányú mozgásegyenlet:![\[0=mg-kt_{e}\sin\alpha\qquad\Rightarrow\qquad t_{e}=\frac{mg}{k\sin\alpha}\]](/images/math/0/d/4/0d4076e8f81c3974ed4db9bd807722b9.png)
Ez alapján a sebesség az idő függvényében![\[ma(t)=kt\cos\alpha\]](/images/math/9/a/b/9ab0c9283324aa1c4f46cc05b83951c9.png)
A felemelkedés pillanatában tehát![\[v(t)=v(0)+\int_{0}^{t}a(t')dt'=\frac{k\cos\alpha}{2m}t^{2}\]](/images/math/6/2/3/62358112b5d2740fb16da9a140c2154f.png)
![\[v(t_{e})=\frac{mg^{2}\cos\alpha}{2k\sin^{2}\alpha}\,.\]](/images/math/1/c/3/1c322b27341dd26c839591aff4ecd6f8.png)
- b) Az elmozdulás az idő függvényében az alábbiak szerint számolható ki. Így a felemelkedésig megtett út
![\[x(t)=x(0)+\int_{0}^{t}v(t')dt'=\frac{k\cos\alpha}{6m}t^{3}\]](/images/math/3/9/3/3938340494128b04fa5ff79245063424.png)
![\[x(t_{e})=\frac{m^{2}g^{3}\cos\alpha}{6k^{2}\sin^{3}\alpha}\,.\]](/images/math/4/2/b/42b113a18fc75fd1672ce06d95aa4348.png)
- a) A testre az
