„Kinematika - 1.3.8” változatai közötti eltérés
A Fizipedia wikiből
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő: Bácsi Ádám]] | [[Kategória:Szerkesztő: Bácsi Ádám]] | ||
| − | [[Kategória: | + | [[Kategória:Mechanika - Mozgástan]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| − | | témakör = | + | | témakör = Mechanika - Mozgástan |
}} | }} | ||
== Feladat == | == Feladat == | ||
A lap 2013. április 22., 16:27-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (1.3.8.) Egy részecske a pozitív
tengely irányába mozog, úgy, hogy sebessége az alábbi törvény szerint változik: 
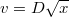, ahol d pozitív állandó. Tételezzük fel, hogy a 
időpontban a részecske az origóban volt. Határozzuk meg
- a) a részecske sebességének és gyorsulásának függését az időtől!
- b) a részecske átlagsebességét, míg az
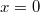pontból az 
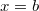pontba jut!
Megoldás
- a) A
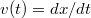összefüggés alapján az 
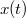függvényre vonatkozó differenciál egyenlet alakban írható. A kezdeti feltétel![\[\frac{dx}{dt}=D\sqrt{x(t)}\]](/images/math/a/8/6/a86d039261e36853c061b05836b5c999.png)
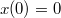. ![\[\frac{1}{\sqrt{x}}\frac{dx}{dt}=D\]](/images/math/4/1/f/41f0a2ded8af6aaed02ba1df07969997.png)
![\[\frac{d}{dt}\left(\frac{1}{2\sqrt{x}}\right)=D\]](/images/math/3/b/8/3b88b34f1357d10c91048e1a6f54b726.png)
ahol![\[\frac{1}{2\sqrt{x}}=Dt+C\,,\]](/images/math/d/5/0/d50d1d18a359a60e77099a8726487320.png)
egy tetszőleges konstans melynek pontos értékét a kezdeti feltétellel illesztjük. A kezdeti feltétel miatt![\[x(t)=\frac{(Dt+c)^{2}}{4}\]](/images/math/c/e/1/ce14ad845ce83cd8ed84edbdf2f5afd8.png)
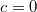, vagyis Ez alapján![\[x(t)=\frac{D^{2}t^{2}}{4}.\]](/images/math/e/0/e/e0ec653121816e657557c7c584f768b5.png)
![\[v(t)=\frac{dx}{dt}=\frac{D^{2}t}{2}\qquad\mbox{és}\qquad a(t)=\frac{dv}{dt}=\frac{D^{2}}{2}\,.\]](/images/math/5/c/3/5c35932b8b593f4579cfad4df4ec0f57.png)
- b) Jelöljük
-vel azt a pillanatot, amikor a részecske az 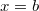pontban van. Így az átlag sebesség![\[x(T)=b\qquad\Rightarrow\qquad T=\frac{2\sqrt{b}}{D}\]](/images/math/b/2/6/b269419b83ea3de04a2ce0689e51456c.png)
![\[v_{atlag}=\frac{b}{T}=\frac{D\sqrt{b}}{2}\,.\]](/images/math/3/3/5/3357662062e58205cc30d3b9e3c4f776.png)
- a) A
