„Erőtan I. - 2.4.1” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Erőtan I. {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő: Bácsi Ádám]] | [[Kategória:Szerkesztő: Bácsi Ádám]] | ||
| − | [[Kategória:Erőtan I.]] | + | [[Kategória:Mechanika - Erőtan I.]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| − | | témakör = Erőtan I. | + | | témakör = Mechanika - Erőtan I. |
}} | }} | ||
== Feladat == | == Feladat == | ||
| 11. sor: | 11. sor: | ||
</wlatex><includeonly><wlatex>{{Útmutatás|content= Energetikai megfontolásokkal határozd meg a golyó sebességét az alsó pontban!}}{{Végeredmény|content= $K=3mg$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content= Energetikai megfontolásokkal határozd meg a golyó sebességét az alsó pontban!}}{{Végeredmény|content= $K=3mg$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: A kezdeti pozícióban a golyó helyzeti energiája a legalsó ponthoz viszonyítva $E_{h}=mgl$. Ezaz energia alakul át mozgási energiává a legalsó pontig történő mozgás során. $$\frac{1}{2}mv^{2}=mgl\qquad\Rightarrow\qquad v=\sqrt{2gl}$$ A legalsó pontban a testre | + | <wlatex>#: A kezdeti pozícióban a golyó helyzeti energiája a legalsó ponthoz viszonyítva $E_{h}=mgl$. Ezaz energia alakul át mozgási energiává a legalsó pontig történő mozgás során. $$\frac{1}{2}mv^{2}=mgl\qquad\Rightarrow\qquad v=\sqrt{2gl}$$ A legalsó pontban a testre függőleges irányú gravitációs erő és kötélerő hat. Az eredő erőnek éppen a centripetális erőnek kell lennie, azaz $$K-mg=m\frac{v^{2}}{l}\qquad\Rightarrow\qquad K=3mg\,.$$ |
| − | + | ||
| − | Az eredő erőnek éppen a centripetális erőnek kell lennie, azaz $$K-mg=m\frac{v^{2}}{l}\qquad\Rightarrow\qquad K=3mg$$ | + | |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 22., 17:06-kori változata
Feladat
- Egy
tömegű golyóból és 
hosszúságú, nyújthatatlan fonálból álló ingát a függőlegestől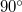 
-kal kitérítünk, majd elengedünk. Mekkora erő feszíti a fonalat a golyó pályájának legalsó pontján való áthaladáskor? (A fonál tömege és a közegelenállás elhanyagolható.)
Megoldás
- A kezdeti pozícióban a golyó helyzeti energiája a legalsó ponthoz viszonyítva
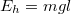. Ezaz energia alakul át mozgási energiává a legalsó pontig történő mozgás során. A legalsó pontban a testre függőleges irányú gravitációs erő és kötélerő hat. Az eredő erőnek éppen a centripetális erőnek kell lennie, azaz![\[\frac{1}{2}mv^{2}=mgl\qquad\Rightarrow\qquad v=\sqrt{2gl}\]](/images/math/6/b/1/6b1944f53bcdb7d18070ad57acc8dc41.png)
![\[K-mg=m\frac{v^{2}}{l}\qquad\Rightarrow\qquad K=3mg\,.\]](/images/math/e/c/a/eca45523df85c83e2317d64a1ef47bde.png)
- A kezdeti pozícióban a golyó helyzeti energiája a legalsó ponthoz viszonyítva
