„Integrálás - Időfüggvények” változatai közötti eltérés

A Fizipedia wikiből
8. sor: 8. sor:
 
== Feladat ==
 
== Feladat ==
 
</noinclude><wlatex>#  
 
</noinclude><wlatex>#  
−
#: a) Az alábbi határozott integrál a változó felső $v$ határ miatt annak függvénye: $$I(v)=\int_{0}^{v}\frac{1}{1-\alpha v'}dv'=t$$ és egyenlő a $t$ időváltozóval. Határozzuk meg a $v(t)$ függvényt!</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)$}}</wlatex></includeonly><noinclude>
+
#: a) Az alábbi határozott integrál a változó felső $v$ határ miatt annak függvénye: $$I(v)=\int_{0}^{v}\frac{1}{1-\alpha v'}dv'=t$$ és egyenlő a $t$ időváltozóval. Határozzuk meg a $v(t)$ függvényt!
 +
#: b) Az alábbi határozott integrál a változó felső $\omega$ határ miatt annak függvénye: $$\alpha t= \int \limits _{\omega _0} ^\omega \frac{1}{\omega '^2} d\omega ' = I(\omega)$$ Határozzuk meg az $\omega(t)$ függvényt!
 +
#: c) Az alábbi határozott integrál a változó $h$ határ miatt annak függvénye: $$I (h) = \int \limits _{h_0} ^h \frac {1}{\sqrt{h '}} dh' = -c t $$ Határozzuk meg a $h(t)$ függvényt!</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)$}} b) $\omega (t) = \frac{ \omega _0}{1 - \omega _0 \alpha t}$ c) $\sqrt{h} = \sqrt{h _0} - \frac{ct}{2}$$ $$h(t) = h_0 + \frac {c^2 t^2 }{4} - c \sqrt { h_0 } \cdot t$</wlatex></includeonly><noinclude>
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>#: a) $$t=\left[-\frac{1}{\alpha}\ln\left(1-\alpha v'\right)\right]^{v}_{0}$$ $$-\alpha t=\ln(1-\alpha v)-\underbrace{\ln 1}_{0}$$ $$e^{-\alpha t}=1-\alpha v$$ $$v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)$$</wlatex>
+
<wlatex>#: a) $$t=\left[-\frac{1}{\alpha}\ln\left(1-\alpha v'\right)\right]^{v}_{0}$$ $$-\alpha t=\ln(1-\alpha v)-\underbrace{\ln 1}_{0}$$ $$e^{-\alpha t}=1-\alpha v$$ $$v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)$$
 +
#: b) $$\alpha t = \left[ - \frac{1}{ \omega '} \right]_ {\omega _0} ^{\omega } = \frac{1}{\omega _0}- \frac{1}{\omega }$$
 +
$$\frac{1}{ \omega } = \frac {1 }{\omega _0} - \alpha t = \frac { 1 - \omega _0 \alpha t }{\omega _0}$$
 +
$$\omega (t) = \frac{ \omega _0}{1 - \omega _0 \alpha t}$$
 +
#: c) $$2\sqrt{h} - 2\sqrt{h _0} = - ct$$ $$\sqrt{h} = \sqrt{h _0} - \frac{ct}{2}$$ $$h(t) = h_0 + \frac {c^2 t^2 }{4} - c \sqrt { h_0 } \cdot t$$</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. május 2., 13:42-kori változata

[rejt] Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája:
  1. Deriválás
  2. Integrálás
  3. Mozgástan
  4. Erőtan I.
  5. Erőtan II.
  6. Munka, energia
  7. Pontrendszerek
  8. Merev testek I.
  9. Merev testek II.
  10. Rugalmasság, folyadékok
  11. Rezgések I.
  12. Rezgések II.
  13. Hullámok
Integrálás
Feladatok listája:
  1. Alapvető integrálok
  2. Területszámítás
  3. Parciális integrálás
  4. Vegyes integrálok
  5. Tömegközéppont számítás
  6. Időfüggvények
  7. Forgástest
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. a) Az alábbi határozott integrál a változó felső \setbox0\hbox{$v$}% \message{//depth:\the\dp0//}% \box0% határ miatt annak függvénye:
    \[I(v)=\int_{0}^{v}\frac{1}{1-\alpha v'}dv'=t\]
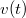    és egyenlő a \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% időváltozóval. Határozzuk meg a \setbox0\hbox{$v(t)$}% \message{//depth:\the\dp0//}% \box0% függvényt!
    b) Az alábbi határozott integrál a változó felső \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0% határ miatt annak függvénye:
    \[\alpha t= \int \limits _{\omega _0} ^\omega \frac{1}{\omega '^2} d\omega ' = I(\omega)\]
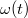    Határozzuk meg az \setbox0\hbox{$\omega(t)$}% \message{//depth:\the\dp0//}% \box0% függvényt!
    c) Az alábbi határozott integrál a változó \setbox0\hbox{$h$}% \message{//depth:\the\dp0//}% \box0% határ miatt annak függvénye:
    \[I (h) = \int \limits _{h_0} ^h \frac {1}{\sqrt{h '}} dh' = -c t \]
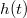    Határozzuk meg a \setbox0\hbox{$h(t)$}% \message{//depth:\the\dp0//}% \box0% függvényt!

Megoldás

  1. a)
    \[t=\left[-\frac{1}{\alpha}\ln\left(1-\alpha v'\right)\right]^{v}_{0}\]
    \[-\alpha t=\ln(1-\alpha v)-\underbrace{\ln 1}_{0}\]
    \[e^{-\alpha t}=1-\alpha v\]
    \[v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)\]
    b)
    \[\alpha t = \left[ - \frac{1}{ \omega '} \right]_ {\omega _0} ^{\omega } = \frac{1}{\omega _0}- \frac{1}{\omega }\]
\[\frac{1}{ \omega } = \frac {1 }{\omega _0} - \alpha t = \frac { 1 - \omega _0 \alpha t }{\omega _0}\]
\[\omega (t) = \frac{ \omega _0}{1 - \omega _0 \alpha t}\]
  1. c)
    \[2\sqrt{h} - 2\sqrt{h _0} = - ct\]
    \[\sqrt{h} = \sqrt{h _0} - \frac{ct}{2}\]
    \[h(t) = h_0 + \frac {c^2 t^2 }{4} - c \sqrt { h_0 } \cdot t\]
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Integrálás_-_Időfüggvények&oldid=9785”