„Integrálás - Vegyes integrálok” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 7. sor: | 7. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Határozzuk meg az alábbi integrálokat lehetőség szerint többféle módszerrel! | + | </noinclude><wlatex># * Határozzuk meg az alábbi integrálokat lehetőség szerint többféle módszerrel! |
#: a) $$\int e^{x}\mbox{sh} x\,dx$$ | #: a) $$\int e^{x}\mbox{sh} x\,dx$$ | ||
#: b) $$\int\frac{1}{x^{2}+3}dx$$ | #: b) $$\int\frac{1}{x^{2}+3}dx$$ | ||
#: c) $$\int_{0}^{\pi}\sin^{3}x\,dx$$ | #: c) $$\int_{0}^{\pi}\sin^{3}x\,dx$$ | ||
| − | #: d) $$\int\frac{\ln (2x)}{x}dx$$</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $$\frac{e^{2x}}{4}-\frac{x}{2}+C$$ b) $$\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C$$ c) $$\frac43$$ | + | #: d) $$\int\frac{\ln (2x)}{x}dx$$</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $$\frac{e^{2x}}{4}-\frac{x}{2}+C$$ b) $$\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C$$ c) $$\frac43$$ d) pl. $$\frac{(\ln 2x)^2}2 +c$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>#: a) $$\int e^{x}\mbox{sh} x\,dx=\frac{e^{2x}}{4}-\frac{x}{2}+C$$ | <wlatex>#: a) $$\int e^{x}\mbox{sh} x\,dx=\frac{e^{2x}}{4}-\frac{x}{2}+C$$ | ||
A lap jelenlegi, 2014. január 9., 16:11-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- * Határozzuk meg az alábbi integrálokat lehetőség szerint többféle módszerrel!
- a)
![\[\int e^{x}\mbox{sh} x\,dx\]](/images/math/c/8/5/c85ec32a9805d564de6b373645ecf759.png)
- b)
![\[\int\frac{1}{x^{2}+3}dx\]](/images/math/1/6/2/1622a50694d6aad64f076ecc09655c73.png)
- c)
![\[\int_{0}^{\pi}\sin^{3}x\,dx\]](/images/math/c/d/b/cdb2462bda9b53c47163fb33bde41542.png)
- d)
![\[\int\frac{\ln (2x)}{x}dx\]](/images/math/f/c/1/fc1e362c99c973096b02ed0a8aa0ee41.png)
- a)
Megoldás
- a)
![\[\int e^{x}\mbox{sh} x\,dx=\frac{e^{2x}}{4}-\frac{x}{2}+C\]](/images/math/c/d/c/cdc40363703b27cf9ac2fc8f728809e9.png)
- b) Mivel
![\[\int\frac{1}{x^{2}+3}dx\]](/images/math/1/6/2/1622a50694d6aad64f076ecc09655c73.png)
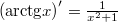 , hasonló megoldást várunk. Az egyetlen eltérés ehhez képest a nevezőben a 3-as.Átalakítva az integrált bevezethetjük az
, hasonló megoldást várunk. Az egyetlen eltérés ehhez képest a nevezőben a 3-as.Átalakítva az integrált bevezethetjük az![\[\frac{1}{3}\int\frac{1}{\frac{x^{2}}{3}+1}dx\]](/images/math/6/0/d/60d76fddfec4146e899adeb250bfd0bb.png)
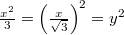 azaz
azaz 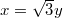 helyettesítést. Ebből a transzformációs képletből: így az átírt integrál
helyettesítést. Ebből a transzformációs képletből: így az átírt integrál![\[\frac{dx}{dy}=\sqrt{3},\]](/images/math/4/6/2/4627bb36f49484989353b30c9296ed4d.png) visszahelyettesítés után végül:
visszahelyettesítés után végül:![\[\frac{1}{3}\int\frac{1}{y^{2}+1}\sqrt{3}dx=\frac{1}{\sqrt{3}}\mbox{arctg}\,y+C\]](/images/math/f/7/9/f79464f3176e2849fc07dfbd72ce2a59.png)
![\[\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C\]](/images/math/1/7/a/17ae43437200f976baf5faea2bdad36f.png)
- c)
![\[\int_{0}^{\pi}\sin^{3}x\,dx=\int_{0}^{\pi}\sin^{2}x\sin x\,dx=\int_{0}^{\pi}\left(1-\cos^{2} x\right)\sin x\,dx=\int_{0}^{\pi}\sin x\,dx-\int_{0}^{\pi}\cos^{2}x\sin x\,dx=\]](/images/math/9/f/8/9f8202c00ad74720163447fda44cb38c.png)
![\[\left[-\cos x\right]^{\pi}_{0}+\left[\frac{\cos^{3} x}{3}\right]^{\pi}_{0}=\frac{4}{3}\]](/images/math/c/d/a/cdae33b69f3b5b4bc50e808f03f95857.png)
- d) Belső függvény deriválttal: tehát a keresett integrál
![\[\frac {d }{dx} \left( \ln 2x \right) ^2 = 2 \ln 2x \cdot \frac{1}{2x} \cdot 2 = \frac {\ln 2x}{x} \cdot 2c,\]](/images/math/d/5/8/d58c059f1c72053fe3bbc1f563126904.png) Helyettesítéssel:
Helyettesítéssel:![\[\frac{(\ln 2x)^2}2 +c.\]](/images/math/7/0/7/707094974ad120fc0e96a53db0377e75.png)
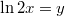 ,
, 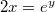 ,
, 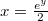 , ebből végül
, ebből végül![\[\frac {dx}{dy} = \frac { e^y}{2}\]](/images/math/4/3/6/43659efb77ac86611b54cefef1acc775.png) Parciális integrálással kétféleképpen is belefoghatunk: ha
Parciális integrálással kétféleképpen is belefoghatunk: ha![\[\int \frac{ \ln 2x}{x} dx = \int \frac {2y}{e^y} dx (y) = \int \frac {2y}{e ^y} \frac { e ^y}{2} dy = \int y dy = \frac {y^2 }{2} +c = \frac {(\ln 2x) ^2}{2} +c\]](/images/math/e/0/9/e093f6175ac31022d451b174f15ee9c9.png)
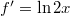 és
és 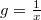 , akkor
, akkor 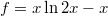 és
és 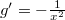 , továbbá amelyben újra megjelent a keresett I integrál. Tovább egyszerűsítve:
, továbbá amelyben újra megjelent a keresett I integrál. Tovább egyszerűsítve:![\[I = \frac { \left( x ln2x -x \right)}{x}+ \int \frac{(x ln2x-x)}{x^2} = ln2x -1 + \int \frac{ln2x}{x} - \int \frac{1}{x},\]](/images/math/8/d/1/8d17951ee8a21f803da1fd7a8de3cd5d.png) azaz I-vel egyszerűsítve
azaz I-vel egyszerűsítve![\[I = ln2x -1 -ln x +I\]](/images/math/f/8/7/f87a9a473b4de91a7066f5e45e6e3b0f.png) Ez látszólag ellentmondás, de csak azért, mert az előbbi sorokban lehagytuk az additív konstanst. Azt is figyelembe véve ez a parciális integrálás nem ellentmondás, csak eredménytelen. Fordított szereposztással azonban eredményre vezet. Ha
Ez látszólag ellentmondás, de csak azért, mert az előbbi sorokban lehagytuk az additív konstanst. Azt is figyelembe véve ez a parciális integrálás nem ellentmondás, csak eredménytelen. Fordított szereposztással azonban eredményre vezet. Ha![\[0 = ln2x -1 -lnx = ln2 + lnx -1 - lnx = ln2 -1 \neq 0.\]](/images/math/c/d/c/cdce20a185702371c75a923949a4ad52.png)
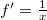 és
és 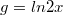 , akkor
, akkor 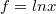 és
és 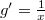 , ezzel az integrál azaz megjelenik egy az eredetihez hasonló típusú integrál. Lényeges eltérés az előző próbálkozáshoz képest, hogy
, ezzel az integrál azaz megjelenik egy az eredetihez hasonló típusú integrál. Lényeges eltérés az előző próbálkozáshoz képest, hogy![\[I = \ln x \cdot \ln 2x - \int \frac {\ln x }{x} dx = \ln x \cdot \ln 2x - I_2,\]](/images/math/3/1/d/31d07624a85658ffe8816186c81daf99.png)
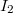 előjele negatív, és a megoldást továbbvezetve rekurzióhoz juthatunk.
előjele negatív, és a megoldást továbbvezetve rekurzióhoz juthatunk. 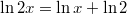 felbontás alapján továbbá Tehát
felbontás alapján továbbá Tehát![\[I=\int \frac {\ln x}{x} + \int \frac {\ln 2}{x}=\int \frac {\ln x}{x} + \ln 2 \cdot \ln x=I_2+ \ln 2 \cdot \ln x\]](/images/math/7/1/5/71562075a833ad048d4ca0a61e44717a.png)
![\[I=\ln x \cdot \ln 2x - I_2 = I_2 + \ln2 \cdot \ln x\]](/images/math/5/1/b/51b7d83bbe7c7152881247d13eaba1e4.png)
![\[2I_2 = \ln x \cdot \ln2x - \ln2 \cdot \ln x\]](/images/math/e/e/6/ee6bd85236bacf6f4180a98bac6aff53.png) Ezt behelyettesítve kapjuk:
Ezt behelyettesítve kapjuk:![\[I_2 =\frac { \ln x \cdot \ln2x}{2} - \frac {\ln2 \ln x }{2}.\]](/images/math/c/7/9/c79f1a4c19d61e5ffedb967c83387ff4.png) a konstans erejéig azonos az előző megoldásokkal.
a konstans erejéig azonos az előző megoldásokkal.![\[I= \frac {\ln x ~\ln 2x}{2}+ \frac {\ln 2 ~ \ln x }{2} = \frac { ( \ln x ) ^2}{2} + \frac { \ln x ~\ln 2 }{2} + \frac {\ln 2 ~\ln x}{2} = \frac {( \ln x ) ^2}{2} + \ln 2 ~ \ln x +c\]](/images/math/6/d/4/6d4a5ed1bba5de04afbd8ad8be0cca7f.png)
- a)