„Kinematika - 1.4.17” változatai közötti eltérés
A Fizipedia wikiből
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
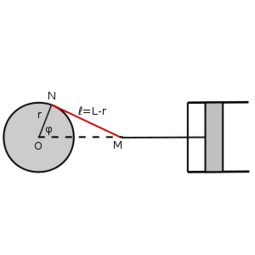
| − | </noinclude><wlatex># (1.4.17) Egy gőzgép hajtókereke egyenletes $\omega$ szögsebességgel forog az $0$ középpontján átmenő tengely körül. A kerék $l$ hosszúságú hajtórúdjának $N$ csuklópontja az $0$-tól $r$ távolságban van, $M$ vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az $M$ pont sebessége abban a pillanatban, amikor $ON$ a vízszintessel $\varphi$ szöget zár be? ($0$ a dugattyú-karral egy egyenesen fekszik.)[[Kép:Kfgy1_03_1_4_17.svg|none| | + | </noinclude><wlatex># (*1.4.17) Egy gőzgép hajtókereke egyenletes $\omega$ szögsebességgel forog az $0$ középpontján átmenő tengely körül. A kerék $l$ hosszúságú hajtórúdjának $N$ csuklópontja az $0$-tól $r$ távolságban van, $M$ vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az $M$ pont sebessége abban a pillanatban, amikor $ON$ a vízszintessel $\varphi$ szöget zár be? ($0$ a dugattyú-karral egy egyenesen fekszik.)[[Kép:Kfgy1_03_1_4_17.svg|none|255px]] |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Az $NOM$ háromszögre cosinus-tételt alkalmazzunk!}}{{Végeredmény|content=$$v(\varphi)=r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{l^{2}-r^{2}\sin^{2}\varphi}}\right]$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=Az $NOM$ háromszögre cosinus-tételt alkalmazzunk!}}{{Végeredmény|content=$$v(\varphi)=r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{l^{2}-r^{2}\sin^{2}\varphi}}\right]$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Vegyük kezdőpillanatnak azt, amikor az $N$ csuklópont az $OM$ egyenesre illeszkedik, vagyis amikor $\varphi=0 | + | <wlatex>#: Vegyük kezdőpillanatnak azt, amikor az $N$ csuklópont az $OM$ egyenesre illeszkedik, vagyis amikor $\varphi=0$, így $\varphi(t)=\omega t$. Az $OM$ szakasz hosszát jelöljük $x(t)$-vel. Ha $O$ a koordinátarendszer origója, akkor $x(t)$ egyben $M$ pont tisztán $x$ tengely menti mozgását is leírja ($y(t)\equiv 0$). Az $NOM$ háromszögre cosinus-tételt alkalmazva $$l^{2}=r^{2}+x(t)^{2}-2rx(t)\cos(\varphi(t))$$ adódik. Ebből a másodfokú egyenletből $$x(t)=r\cos(\omega t)+\sqrt{l^{2}-r^{2}\sin^{2}(\omega t)}$$ eredményre jutunk. Az $M$ pont sebessége $$v(t)=\frac{dx}{dt}=-r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{l^{2}-r^{2}\sin^{2}\varphi}}\right]\,.$$ Elkerülhető a másodfokú egyenlet, ha az $OM$-re merőleges magassággal két derékszögú háromszögre osztjuk az $ONM$ háromszöget. |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2015. március 6., 16:21-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*1.4.17) Egy gőzgép hajtókereke egyenletes
szögsebességgel forog az 
középpontján átmenő tengely körül. A kerék 
hosszúságú hajtórúdjának 
csuklópontja az -tól 
távolságban van, 
vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az pont sebessége abban a pillanatban, amikor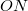 
a vízszintessel 
szöget zár be? ( a dugattyú-karral egy egyenesen fekszik.)
Megoldás
- Vegyük kezdőpillanatnak azt, amikor az csuklópont az
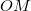egyenesre illeszkedik, vagyis amikor 
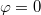, így 
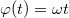. Az 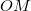szakasz hosszát jelöljük 
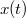-vel. Ha 
a koordinátarendszer origója, akkor 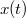egyben pont tisztán 
tengely menti mozgását is leírja (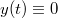
). Az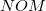 
háromszögre cosinus-tételt alkalmazva adódik. Ebből a másodfokú egyenletből![\[l^{2}=r^{2}+x(t)^{2}-2rx(t)\cos(\varphi(t))\]](/images/math/8/d/e/8decdc02303386aa8879ba5da1c77fce.png)
eredményre jutunk. Az![\[x(t)=r\cos(\omega t)+\sqrt{l^{2}-r^{2}\sin^{2}(\omega t)}\]](/images/math/6/f/7/6f7752a14d0369e87945fb3bcffcfa0b.png)
pont sebessége Elkerülhető a másodfokú egyenlet, ha az![\[v(t)=\frac{dx}{dt}=-r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{l^{2}-r^{2}\sin^{2}\varphi}}\right]\,.\]](/images/math/4/5/4/4543111ba89523b6eaff698faa490847.png)
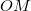-re merőleges magassággal két derékszögú háromszögre osztjuk az 
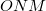háromszöget.
- Vegyük kezdőpillanatnak azt, amikor az
