„Kinematika - Változó mozgás” változatai közötti eltérés

A Fizipedia wikiből
(→‎Megoldás)
 
(egy szerkesztő egy közbeeső változata nincs mutatva)
14. sor: 14. sor:
  
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>#: a) Az ábráról leolvasható a $v(t)$ függvény. $$v(t)=\left\{\begin{array}{ccc} v_{0}+v_{1}\cos(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ v_{0}+v_{1} & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\qquad\qquad v_{0}=3\,\mathrm{\frac{m}{s}}\qquad v_{1}=2\,\mathrm{\frac{m}{s}}\qquad \omega=\frac{\pi}{2}\frac{1}{\,\mathrm{s}}$$
+
<wlatex>#: a) Az ábráról leolvasható a $v(t)$ függvény. $$v(t)=\left\{\begin{array}{ccc} v_{1}+v_{2}\cos(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ v_{1}+v_{2} & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\qquad\qquad v_{1}=3\,\mathrm{\frac{m}{s}}\qquad v_{2}=2\,\mathrm{\frac{m}{s}}\qquad \omega=\frac{\pi}{2}\frac{1}{\,\mathrm{s}}$$
−
#: b) $$a(t)=\frac{dv}{dt}=\left\{\begin{array}{ccc} -v_{1}\omega\sin(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ 0 & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.$$
+
#: b) $$a(t)=\frac{dv}{dt}=\left\{\begin{array}{ccc} -v_{2}\omega\sin(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ 0 & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.$$
−
#: c) $$x(t)=x(0)+\int_{0}^{t}v(t')dt'=\left\{\begin{array}{ccc} v_{0} t + \frac{v_{1}}{\omega}\sin(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\
+
#: c) $$x(t)=x(0)+\int_{0}^{t}v(t')dt'=\left\{\begin{array}{ccc} v_{1} t + \frac{v_{2}}{\omega}\sin(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\
−
  (v_{0}+v_{1})t - v_{1}T & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\,$$ ahol $T=2\pi/\omega=4\,\mathrm{s}$ a periódusidő.
+
  (v_{1}+v_{2})t - v_{2}T & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\,$$ ahol $T=2\pi/\omega=4\,\mathrm{s}$ a periódusidő.
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2016. szeptember 21., 09:47-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája:
  1. Deriválás
  2. Integrálás
  3. Mozgástan
  4. Erőtan I.
  5. Erőtan II.
  6. Munka, energia
  7. Pontrendszerek
  8. Merev testek I.
  9. Merev testek II.
  10. Rugalmasság, folyadékok
  11. Rezgések I.
  12. Rezgések II.
  13. Hullámok
Mechanika - Mozgástan
Feladatok listája:
  1. Kinematika - 1.1.7
  2. Kinematika - 1.2.6
  3. Kinematika - 1.2.8
  4. Kinematika - 1.3.1
  5. Kinematika - Változó mozgás
  6. Kinematika - 1.3.8
  7. Kinematika - 1.4.6
  8. Kinematika - 1.4.7
  9. Kinematika - 1.4.10
  10. Kinematika - 1.4.17
  11. Kinematika - 1.4.18
  12. Kinematika - 1.4.20
  13. Kinematika - 1.4.23
  14. Kinematika - Ferde hajítás
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

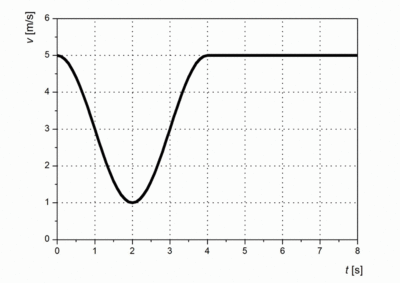
  1. (*1.2.22) Egy test a vizsgált időtartam első felében harmonikus rezgést végez, a második felében egyenletesen mozog. Mozgásának sebesség-idő grafikonja az alábbi ábrán látható.
    Kfgy1-1.2.22.gif
    a) Írja fel a sebességet az idő függvényében mindkét tartományon!
    b) Határozza meg a gyorsulás-idő függvényt képlettel!
    c) Határozza meg az 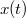\setbox0\hbox{$x(t)$}% \message{//depth:\the\dp0//}% \box0% függvényt, ha a test a 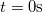\setbox0\hbox{$t=0\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0% időpillanatban az origóban volt!

Megoldás

  1. a) Az ábráról leolvasható a 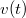\setbox0\hbox{$v(t)$}% \message{//depth:\the\dp0//}% \box0% függvény.
    \[v(t)=\left\{\begin{array}{ccc} v_{1}+v_{2}\cos(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ v_{1}+v_{2} & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\qquad\qquad v_{1}=3\,\mathrm{\frac{m}{s}}\qquad v_{2}=2\,\mathrm{\frac{m}{s}}\qquad \omega=\frac{\pi}{2}\frac{1}{\,\mathrm{s}}\]
    b)
    \[a(t)=\frac{dv}{dt}=\left\{\begin{array}{ccc} -v_{2}\omega\sin(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ 0 & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\]
    c)
    \[x(t)=x(0)+\int_{0}^{t}v(t')dt'=\left\{\begin{array}{ccc} v_{1} t + \frac{v_{2}}{\omega}\sin(\omega t) & \mbox{ha} & 0<t<4\,\mathrm{s} \\ (v_{1}+v_{2})t - v_{2}T & \mbox{ha} & 4\,\mathrm{s}<t\end{array}\right.\,\]
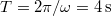    ahol \setbox0\hbox{$T=2\pi/\omega=4\,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0% a periódusidő.
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Kinematika_-_Változó_mozgás&oldid=19246”