„Mechanika - Mozgástan” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gyakorlat 1. |…”) |
|||
| (2 szerkesztő 6 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladatok == | == Feladatok == | ||
| − | {{: | + | {{:Kinematika - 1.1.7}}{{Megoldás|link=Kinematika - 1.1.7}} |
| − | {{: | + | {{:Kinematika - 1.2.6}}{{Megoldás|link=Kinematika - 1.2.6}} |
| − | {{: | + | {{:Kinematika - 1.2.8}}{{Megoldás|link=Kinematika - 1.2.8}} |
| − | {{: | + | <!-- {{:Kinematika - 1.2.17}}{{Megoldás|link=Kinematika - 1.2.17}} --> |
| − | {{: | + | {{:Kinematika - 1.3.1}}{{Megoldás|link=Kinematika - 1.3.1}} |
| − | {{: | + | {{:Kinematika - Változó mozgás}}{{Megoldás|link=Kinematika - Változó mozgás}} |
| − | {{: | + | {{:Kinematika - 1.3.8}}{{Megoldás|link=Kinematika - 1.3.8}} |
| − | {{: | + | {{:Kinematika - 1.4.6}}{{Megoldás|link=Kinematika - 1.4.6}} |
| − | {{: | + | {{:Kinematika - 1.4.7}}{{Megoldás|link=Kinematika - 1.4.7}} |
| − | {{: | + | {{:Kinematika - 1.4.10}}{{Megoldás|link=Kinematika - 1.4.10}} |
| − | {{: | + | {{:Kinematika - 1.4.17}}{{Megoldás|link=Kinematika - 1.4.17}} |
| − | {{: | + | {{:Kinematika - 1.4.18}}{{Megoldás|link=Kinematika - 1.4.18}} |
| − | {{: | + | {{:Kinematika - 1.4.20}}{{Megoldás|link=Kinematika - 1.4.20}} |
| − | {{: | + | {{:Kinematika - 1.4.23}}{{Megoldás|link=Kinematika - 1.4.23}} |
| + | {{:Kinematika - Ferde hajítás}}{{Megoldás|link=Kinematika - Ferde hajítás}} | ||
A lap jelenlegi, 2014. szeptember 23., 20:21-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- (*1.1.7.) Két párhuzamosan haladó sínpáron egy-egy vonat halad egymás felé. Az egyik vonat sebessége
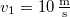 , a másiké
, a másiké 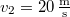 . A gyorsabban haladó vonat füttyjelet bocsát ki, melyet a vonat vezetője
. A gyorsabban haladó vonat füttyjelet bocsát ki, melyet a vonat vezetője 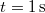 hosszúnak észlel. Milyen hosszúnak méri a füttyjelet a töltésen álló, illetve a közeledő vonaton ülő megfigyelő? (hangsebesség:
hosszúnak észlel. Milyen hosszúnak méri a füttyjelet a töltésen álló, illetve a közeledő vonaton ülő megfigyelő? (hangsebesség: 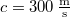 )
)
- (1.2.6.) Egy testet függőleges irányban
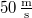 sebességgel feldobunk. Milyen magasra emelkedik
sebességgel feldobunk. Milyen magasra emelkedik 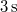 alatt? Mekkora a legnagyobb magasság, amit elér? Mennyi ideig emelkedik felfelé? Mennyi idő múlva esik vissza a földre? (
alatt? Mekkora a legnagyobb magasság, amit elér? Mennyi ideig emelkedik felfelé? Mennyi idő múlva esik vissza a földre? (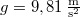 )
)
- (*1.2.8.) Egy motorkerékpáros állandó
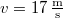 sebességgel halad el a rendőr előtt, aki azonnal észreveszi, hogy a motoros bizonyos szabálysértést követett el, és ezért utol kell érnie. Négy másodperccel később a rendőr üldözni kezdi a motorost, állóhelyből indulva, és állandó gyorsulással mozogva. őrhelyétől mérve
sebességgel halad el a rendőr előtt, aki azonnal észreveszi, hogy a motoros bizonyos szabálysértést követett el, és ezért utol kell érnie. Négy másodperccel később a rendőr üldözni kezdi a motorost, állóhelyből indulva, és állandó gyorsulással mozogva. őrhelyétől mérve 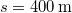 távolságban éri utól a motorost. Mennyi időt fordított a rendőr az üldözésre? Mekkora volt a gyorsulása? Mekkora sebességgel haladt a rendőr a motoros beérésekor?
távolságban éri utól a motorost. Mennyi időt fordított a rendőr az üldözésre? Mekkora volt a gyorsulása? Mekkora sebességgel haladt a rendőr a motoros beérésekor?
- (1.3.1) Az
 tengelyen mozgó tömegpont gyorsulása az idő függvényében az 1.3.1. ábrán látható.
tengelyen mozgó tömegpont gyorsulása az idő függvényében az 1.3.1. ábrán látható.
- a) Ábrázolja a tömegpont sebességét az idő függvényében, ha a kezdeti sebesség
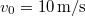 !
!
- b) Határozza meg a tömegpont helyét a
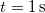 és
és 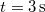 időpillanatokban, ha a tömegpont
időpillanatokban, ha a tömegpont  -ban az
-ban az 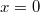 pontban volt!
pontban volt!
- c) Mekkora a tömegpont átlagsebessége a
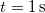 és a
és a 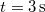 közötti időintervallumban?
közötti időintervallumban?
- a) Ábrázolja a tömegpont sebességét az idő függvényében, ha a kezdeti sebesség
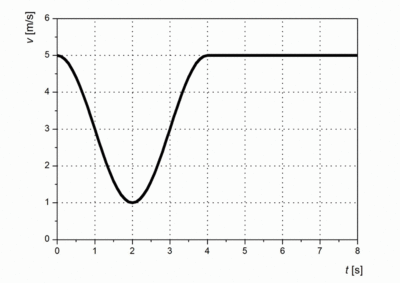
- (*1.2.22) Egy test a vizsgált időtartam első felében harmonikus rezgést végez, a második felében egyenletesen mozog. Mozgásának sebesség-idő grafikonja az alábbi ábrán látható.
- a) Írja fel a sebességet az idő függvényében mindkét tartományon!
- b) Határozza meg a gyorsulás-idő függvényt képlettel!
- c) Határozza meg az
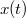 függvényt, ha a test a
függvényt, ha a test a 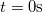 időpillanatban az origóban volt!
időpillanatban az origóban volt!
- (*1.3.8.) Egy részecske a pozitív
 tengely irányába mozog, úgy, hogy sebessége az alábbi törvény szerint változik:
tengely irányába mozog, úgy, hogy sebessége az alábbi törvény szerint változik: 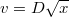 , ahol d pozitív állandó. Tételezzük fel, hogy a
, ahol d pozitív állandó. Tételezzük fel, hogy a  időpontban a részecske az origóban volt. Határozzuk meg
időpontban a részecske az origóban volt. Határozzuk meg
- a) a részecske sebességének és gyorsulásának függését az időtől!
- b) a részecske átlagsebességét, míg az
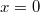 pontból az
pontból az 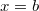 pontba jut!
pontba jut!
- (1.4.6) Egy mozgó pont helyvektorának komponensei:
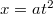 ,
, 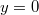 és
és 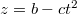 . Határozzuk meg a pont pályáját, sebességét és gyorsulását, valamint azt az időtartamot, amely alatt a pont a pályának a koordináta-tengelyek közötti szakaszát megteszi. Legyen például:
. Határozzuk meg a pont pályáját, sebességét és gyorsulását, valamint azt az időtartamot, amely alatt a pont a pályának a koordináta-tengelyek közötti szakaszát megteszi. Legyen például: 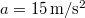 ,
, 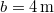 és
és 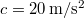 .
.
- (*1.4.7 alapján) Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le:
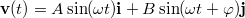 .
.
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
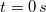 időpontban a test az
időpontban a test az 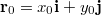 koordinátájú pontban tartózkodott!
koordinátájú pontban tartózkodott!
- b) Határozza meg a test gyorsulásvektorát az idő függvényében!
- c) Milyen pályán mozog a test, ha
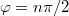 valamilyen
valamilyen  egész számmal?
egész számmal?
- d) Amennyiben
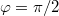 , úgy adjuk meg a pálya görbületi sugarát a
, úgy adjuk meg a pálya görbületi sugarát a 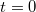 időponthoz tartozó helyen.
időponthoz tartozó helyen.
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
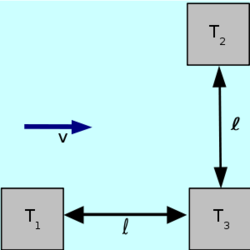
- (*1.4.10) Folyóvízben három tutaj van lehorgonyozva.
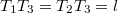 , irányuk egymásra merőleges. A víz
, irányuk egymásra merőleges. A víz 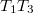 irányában folyik
irányában folyik  sebességgel. Két gyorsúszó azonos, a vízhez képest
sebességgel. Két gyorsúszó azonos, a vízhez képest 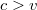 sebességgel a
sebességgel a 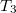 tutajról egyszerre indulnak, az egyik a
tutajról egyszerre indulnak, az egyik a 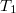 a másik a
a másik a 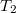 felé, ezeket megérintve visszatérnek
felé, ezeket megérintve visszatérnek 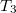 -hoz. Melyik ér vissza előbb, és mennyivel késik a másik?
-hoz. Melyik ér vissza előbb, és mennyivel késik a másik?
- (*1.4.17) Egy gőzgép hajtókereke egyenletes
 szögsebességgel forog az
szögsebességgel forog az  középpontján átmenő tengely körül. A kerék
középpontján átmenő tengely körül. A kerék  hosszúságú hajtórúdjának
hosszúságú hajtórúdjának  csuklópontja az
csuklópontja az  -tól
-tól  távolságban van,
távolságban van,  vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az
vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az  pont sebessége abban a pillanatban, amikor
pont sebessége abban a pillanatban, amikor 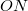 a vízszintessel
a vízszintessel  szöget zár be? (
szöget zár be? ( a dugattyú-karral egy egyenesen fekszik.)
a dugattyú-karral egy egyenesen fekszik.)
- (1.4.18) Egy vékony egyenes cső
 pontja körül állandó
pontja körül állandó  szögsebességgel forog vízszintes síkban. A csőben egy golyó mozog a csőhöz képest állandó
szögsebességgel forog vízszintes síkban. A csőben egy golyó mozog a csőhöz képest állandó 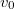 sebességgel. Milyen pályát ír le a golyó a csövön kívül álló megfigyelőhöz képest és mekkora a sebesség nagysága, mint az idő függvénye?
sebességgel. Milyen pályát ír le a golyó a csövön kívül álló megfigyelőhöz képest és mekkora a sebesség nagysága, mint az idő függvénye?
- (*1.4.20) Egy ember a tó partján sétálva a tóban egy fuldoklót vesz észre. A fuldokló a parttól
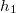 , az ember
, az ember 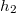 távolságban van. A fuldokló és a mentésére siető távolsága
távolságban van. A fuldokló és a mentésére siető távolsága  . Milyen úton haladjon a mentésre siető ember, hogy a fuldoklót leghamarabb elérje, ha a parton futva
. Milyen úton haladjon a mentésre siető ember, hogy a fuldoklót leghamarabb elérje, ha a parton futva 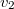 , a vízben úszva
, a vízben úszva 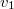 sebességgel tud haladni?
sebességgel tud haladni?
- (*1.4.23) Egy aknavetővel a völgyből
 magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége
magasságú fennsíkra tüzelnek. (1.4.23. ábra). A fennsíktól milyen távolságban kell felállítani az aknavetőt, hogy a lövedék a fennsík szélétől a legmesszebbre repüljön? Mekkora ez a távolság? Milyen szögben kell lőni? A lövedék kezdeti sebessége 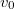 .
.
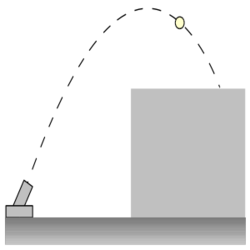
- Egy testet vízszintes terepen, a felszínnel
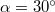 -os szöget bezáróan,
-os szöget bezáróan, 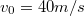 sebességgel lövünk ki. Milyen messzire csapódik be a test a talajba a kilövés helyétől? Milyen magasra jut el mozgása során? Mekkora a pályája görbületi sugara a kilövés helyén, ill. a pálya tetőpontján?(
sebességgel lövünk ki. Milyen messzire csapódik be a test a talajba a kilövés helyétől? Milyen magasra jut el mozgása során? Mekkora a pályája görbületi sugara a kilövés helyén, ill. a pálya tetőpontján?(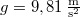 )
)
![\[t_{km}=\frac{28}{30}\,\mathrm{s}\]](/images/math/d/a/a/daadb30d0aab190625d6fd66baa88fdf.png)
![\[t_{mv}=\frac{28}{31}\,\mathrm{s}\]](/images/math/3/c/8/3c88c5c2a4af314c492b65bf4b02918c.png)
![\[h(t_{1})=105,855\,\mathrm{m}\]](/images/math/9/8/0/98006297470c3b6a5492750401e2cc9d.png)
![\[T_{\mathrm{em}}=5,097\,\mathrm{s}\]](/images/math/f/c/4/fc4b2acaadc3fbe34913ee8d0e2baafe.png)
![\[h_{\mathrm{max}}=127,42\,\mathrm{m}\]](/images/math/1/7/9/17984e9c807af34b17790258c4a8d6b8.png)
![\[T_{\mathrm{ve}}=10,194\,\mathrm{s}\]](/images/math/5/2/e/52e8a22c2c21feb15a2804f220e62446.png)
![\[T=19,53 \,\mathrm{s}\]](/images/math/6/7/e/67e546ecf8d513edc22e4504b00714da.png)
![\[a=2,1\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/3/6/c/36c0fa90d182327b93e378ca5470e33a.png)
![\[v_{max}=41,01\,\mathrm{\frac{m}{s}}\]](/images/math/0/5/0/050a276a092dc2b99b00a3db34b36698.png)
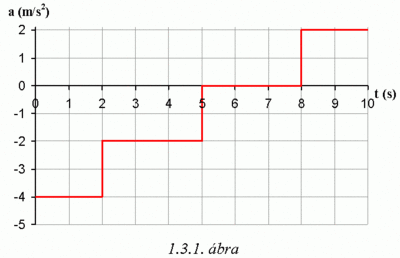
![\[x(t=1\,\mathrm{s})=8\,\mathrm{m}\qquad\mbox{és}\qquad x(t=3\,\mathrm{s})=13\,\mathrm{m}\]](/images/math/1/d/9/1d92104ff21ed0f944a94dd313184e0b.png)
![\[v_{\mbox{átl}}=2,5\,\mathrm{\frac{m}{s}}\]](/images/math/0/1/5/0151fed8f7ee34d0bac7b4dddd29ba0c.png)
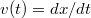 összefüggés alapján írjuk fel az
összefüggés alapján írjuk fel az ![\[v(t)=\frac{dx}{dt}=\frac{D^{2}t}{2}\qquad\mbox{és}\qquad a(t)=\frac{dv}{dt}=\frac{D^{2}}{2}\,.\]](/images/math/5/c/3/5c35932b8b593f4579cfad4df4ec0f57.png)
![\[v_{atlag}=\frac{b}{T}=\frac{D\sqrt{b}}{2}\,.\]](/images/math/3/3/5/3357662062e58205cc30d3b9e3c4f776.png)
![\[v_{x}(t)=\frac{dx}{dt}=2at\]](/images/math/e/c/5/ec5a9a0f6aa65e5f9c123c0e560c6080.png)
![\[v_{y}(t)=\frac{dy}{dt}=0\]](/images/math/8/c/e/8cecc42d71c399cdfd95e9b2432f3374.png)
![\[v_{z}(t)=\frac{dz}{dt}=-2ct\]](/images/math/b/5/5/b55c511a3c496794e1561599ce3f5669.png)
![\[a_{x}(t)=\frac{dv_{x}}{dt}=2a\]](/images/math/3/b/a/3ba61228431454ebf2c3bb9e3061726f.png)
![\[a_{y}(t)=\frac{dv_{y}}{dt}=0\]](/images/math/8/6/c/86cf03285f52a55c0c9e82111950f622.png)
![\[a_{z}(t)=\frac{dv_{z}}{dt}=-2c\]](/images/math/1/1/6/116e9872f2717798b24eba10b43cf067.png)
![\[T=\frac{1}{\sqrt{5}}\,\mathrm{s}\]](/images/math/4/7/a/47a615343d494770a174a8c68461644d.png)
![\[\mathbf{r}(t)=\left(x_{0}+\frac{A}{\omega}-\frac{A}{\omega}\cos(\omega t)\right)\mathbf{i} +\left( y_{0}+\frac{B}{\omega}\cos\varphi- \frac{B}{\omega}\cos(\omega t+\varphi)\right)\mathbf{j}\]](/images/math/f/6/0/f6040af91a503d71c967cfcd88b7ad15.png)
![\[\mathbf{a}(t)=\frac{d\mathbf{v}}{dt}=A\omega\cos(\omega t)\mathbf{i} + B\omega\cos(\omega t+\varphi)\mathbf{j}\]](/images/math/7/7/3/773077855448f6930e66c3cd3d40a012.png)
![\[ \phantom{a} \]](/images/math/9/4/3/943e36a2c1f8ac3b616b1b6f372704ca.png)
![\[R = \frac{B^2}{A \omega} \]](/images/math/4/c/d/4cdb0376f93d4374b0de665d21cb013e.png)
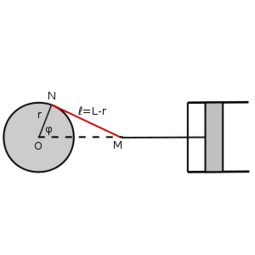
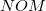 háromszögre cosinus-tételt alkalmazzunk!
háromszögre cosinus-tételt alkalmazzunk! ![\[v(\varphi)=r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{l^{2}-r^{2}\sin^{2}\varphi}}\right]\]](/images/math/6/0/9/6092a2866d0201a1853d0abdba7e6e76.png)

![\[x(t)=r(t)\cos\varphi(t)=|r_{0}-v_{0}t|\cos(\omega t)\]](/images/math/1/b/5/1b54f1253d5a11bc70d46623d4bc8d3f.png)
![\[y(t)=r(t)\sin\varphi(t)=|r_{0}-v_{0}t|\sin(\omega t)\]](/images/math/0/1/2/01251920eb548f27d48bedaeac6bce78.png)
![\[v_{x}(t)=\frac{dx}{dt}=v_{0}\,\mathrm{sgn}(v_{0}t-r_{0})\cos(\omega t)-\omega|r_{0}-v_{0}t|\sin(\omega t)\]](/images/math/c/6/8/c68477d3eb2712b303f188963a7ca762.png)
![\[v_{y}(t)=\frac{dy}{dt}=v_{0}\mathrm{sgn}\,(v_{0}t-r_{0})\sin(\omega t)+\omega|r_{0}-v_{0}t|\cos(\omega t)\]](/images/math/f/2/5/f250fb4680228cdc9488be1131f2a783.png)
![\[\varphi=\arccos\sqrt{\frac{1}{2}-\frac{hg}{v_{0}^{2}}}\]](/images/math/c/b/3/cb3a2e723a373e2c2b55afd5e5011270.png)
![\[D=\frac{v_{0}^{2}}{g}-2h\,.\]](/images/math/6/4/9/64909bf4299497b17ab066ed1374ca88.png)
![\[ d = \frac{2 v_0^2 \sin (\alpha) \cos (\alpha)}{g} = 141.3m\]](/images/math/7/f/1/7f1543ad5182397448e27a92c6a0ff94.png)
![\[h = \frac{v_0^2 \sin^2 (\alpha)}{2 g} = 20.39m \]](/images/math/5/4/2/5424fa15932748977d83bf7c104e7ecd.png)
![\[R_{start} = \frac{v_0^2}{g \cos(\alpha)} = 188.3 m\]](/images/math/3/3/c/33cfdb6089507a854a71eb5b8a7bec9c.png)
![\[R_{fent} = \frac{v_0^2 \cos^2(\alpha)}{g} = 122.3 m\]](/images/math/5/0/c/50c0feb5e847b8e73e9df3775d5fd810.png)