„Erőtan I. - 2.1.4” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Kinematika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| (egy szerkesztő 6 közbeeső változata nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő: Bácsi Ádám]] | [[Kategória:Szerkesztő: Bácsi Ádám]] | ||
| − | [[Kategória: | + | [[Kategória:Mechanika - Erőtan I.]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| − | | témakör = Erőtan I. | + | | témakör = Mechanika - Erőtan I. |
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy autót $4\,\mathrm{\frac{m}{s^{2}}}$ gyorsulással indítanak. A vezető az 5. másodperc végén akadályt pillant meg és $1 \,\mathrm{s}$ telik el a fékezés megkezdéséig. Hány métert halad az autó az akadály megpillantása után, ha a fék a kerekeket teljesen lefékezi? Mennyit haladt volna, ha a vezető azonnal fékez? A lefékezett autó és az úttest közötti súrlódási tényező $0,5$. | + | </noinclude><wlatex># (2.1.4) Egy autót $4\,\mathrm{\frac{m}{s^{2}}}$ gyorsulással indítanak. A vezető az 5. másodperc végén akadályt pillant meg és $1 \,\mathrm{s}$ telik el a fékezés megkezdéséig. Hány métert halad az autó az akadály megpillantása után, ha a fék a kerekeket teljesen lefékezi? Mennyit haladt volna, ha a vezető azonnal fékez? A lefékezett autó és az úttest közötti súrlódási tényező $0,5$. |
</wlatex><includeonly><wlatex>{{Végeredmény|content=$s_{e}=79,6\,\mathrm{m}$ <br> $s'=40 \,\mathrm{m}$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$s_{e}=79,6\,\mathrm{m}$ <br> $s'=40 \,\mathrm{m}$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Ha $t$ ideig gyorsult az autó egyenletes $a$ gyorsulással, akkor a gyorsulás után a sebessége $v=at$. Ezután kezdődik meg a fékezés, melynek során | + | <wlatex>#: Ha $t$ ideig gyorsult az autó egyenletes $a$ gyorsulással, akkor a gyorsulás után a sebessége $v=at$. Ezután kezdődik meg a fékezés, melynek során a függőleges irányú gravitációs és nyomóerő mellett egy vízszintes irányú súrlódási erő is megjelenik. Függőleges irányban az autó egyensúlyban van, ezért $N=F_{g}=mg$. Vízszintes irányban van gyarsulása az autónak, melyet $m a_{f}=S$ határoz meg. A súrlódási erőt $S=\mu N$ szerint számolhatjuk ki. Ezek alapján $a_{f}=\mu g$. <br> A megálláshoz szükséges idő $t_{f}=\frac{v}{a_{f}}$. Az ezalatt megtett út pedig $$s=\frac{a_{f}}{2}t_{f}^{2}=\frac{a^{2}}{2\mu g}t^{2}$$ A feladat első kérdése arra vonatkozik, amikor az autó az akadály megpillantása előtti $t_{0}=5\,\mathrm{s}$ időtartam után még $\Delta t=1\,\mathrm{s}$ ideig gyorsult. Ekkor fékezéstől a megállásig $$s_{u}=\frac{a^{2}}{2\mu g}(t_{0}+\Delta t)^{2}=57,6\,\mathrm{m}$$ utat tesz meg. A fékezés előtti $\Delta t$ idő alatt pedig $$s_{e}=\frac{a}{2}\left((t_{0}+\Delta t)^{2}-t_{0}^{2}\right)=22\,\mathrm{m}$$ utat tett meg. Így összesen az első esetben az autó $79,6\,\mathrm{m}$ tesz meg az akadály megpillantásától a teljes megállásig. <br> A másik esetben csak $t_{0}$ ideig gyorsul az autó, és rögtön megkezdődik a fékezés. Ekkor $$s'=\frac{a^{2}}{2\mu g}t_{0}^{2}=40 \,\mathrm{m}$$ utat tesz meg az autó. |
| − | + | ||
| − | Függőleges irányban az autó egyensúlyban van, ezért $N=F_{g}=mg$. Vízszintes irányban van gyarsulása az autónak, melyet $m a_{f}=S$ határoz meg. A súrlódási erőt $S=\mu N$ szerint számolhatjuk ki. Ezek alapján $a_{f}=\mu g$. <br> A megálláshoz szükséges idő $t_{f}=\frac{v}{a_{f}}$. Az ezalatt megtett út pedig $$s=\frac{a_{f}}{2}t_{f}^{2}=\frac{a^{2}}{2\mu g}t^{2}$$ A feladat első kérdése arra vonatkozik, amikor az autó az akadály megpillantása előtti $t_{0}=5\,\mathrm{s}$ időtartam után még $\Delta t=1\,\mathrm{s}$ ideig gyorsult. Ekkor fékezéstől a megállásig $$s_{u}=\frac{a^{2}}{2\mu g}(t_{0}+\Delta t)^{2}=57,6\,\mathrm{m}$$ utat tesz meg. A fékezés előtti $\Delta t$ idő alatt pedig $$s_{e}=\frac{a}{2}\left((t_{0}+\Delta t)^{2}-t_{0}^{2}\right)=22\,\mathrm{m}$$ utat tett meg. Így összesen az első esetben az autó $79,6\,\mathrm{m}$ tesz meg az akadály megpillantásától a teljes megállásig. <br> A másik esetben csak $t_{0}$ ideig gyorsul az autó, és rögtön megkezdődik a fékezés. Ekkor $$s'=\frac{a^{2}}{2\mu g}t_{0}^{2}=40 \,\mathrm{m}$$ utat tesz meg az autó. | + | |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 27., 21:12-kori változata
Feladat
- (2.1.4) Egy autót
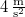gyorsulással indítanak. A vezető az 5. másodperc végén akadályt pillant meg és 
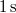telik el a fékezés megkezdéséig. Hány métert halad az autó az akadály megpillantása után, ha a fék a kerekeket teljesen lefékezi? Mennyit haladt volna, ha a vezető azonnal fékez? A lefékezett autó és az úttest közötti súrlódási tényező 
.
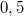Megoldás
- Ha
ideig gyorsult az autó egyenletes 
gyorsulással, akkor a gyorsulás után a sebessége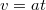 
. Ezután kezdődik meg a fékezés, melynek során a függőleges irányú gravitációs és nyomóerő mellett egy vízszintes irányú súrlódási erő is megjelenik. Függőleges irányban az autó egyensúlyban van, ezért 
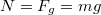. Vízszintes irányban van gyarsulása az autónak, melyet 
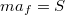határoz meg. A súrlódási erőt 
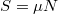szerint számolhatjuk ki. Ezek alapján 
.
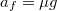A megálláshoz szükséges idő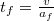
. Az ezalatt megtett út pedig A feladat első kérdése arra vonatkozik, amikor az autó az akadály megpillantása előtti![\[s=\frac{a_{f}}{2}t_{f}^{2}=\frac{a^{2}}{2\mu g}t^{2}\]](/images/math/9/f/b/9fb9e6e5573467352c5da8a0fbef61d1.png)
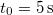időtartam után még 
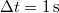ideig gyorsult. Ekkor fékezéstől a megállásig utat tesz meg. A fékezés előtti![\[s_{u}=\frac{a^{2}}{2\mu g}(t_{0}+\Delta t)^{2}=57,6\,\mathrm{m}\]](/images/math/b/9/e/b9e18ab08d4e3c4ec8be7ba8fcc35cbb.png)
idő alatt pedig utat tett meg. Így összesen az első esetben az autó![\[s_{e}=\frac{a}{2}\left((t_{0}+\Delta t)^{2}-t_{0}^{2}\right)=22\,\mathrm{m}\]](/images/math/6/f/e/6fe4ba40ff2dcd22303e41487d5a2c23.png)
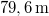tesz meg az akadály megpillantásától a teljes megállásig.
A másik esetben csak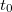
ideig gyorsul az autó, és rögtön megkezdődik a fékezés. Ekkor utat tesz meg az autó.![\[s'=\frac{a^{2}}{2\mu g}t_{0}^{2}=40 \,\mathrm{m}\]](/images/math/2/4/8/2486594e5060c0a04e60dd529103eeaa.png)
- Ha
