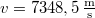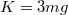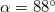„Mechanika - Erőtan I.” változatai közötti eltérés
A Fizipedia wikiből
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 23. sor: | 23. sor: | ||
{{:Erőtan I. - 2.4.4}}{{Megoldás|link=Erőtan I. - 2.4.4}} | {{:Erőtan I. - 2.4.4}}{{Megoldás|link=Erőtan I. - 2.4.4}} | ||
{{:Erőtan I. - 2.4.7}}{{Megoldás|link=Erőtan I. - 2.4.7}} | {{:Erőtan I. - 2.4.7}}{{Megoldás|link=Erőtan I. - 2.4.7}} | ||
| + | {{:Erőtan I. - Harmonikus rezgés gravitációs térben}}{{Megoldás|link=Erőtan I. - Harmonikus rezgés gravitációs térben}} | ||
| + | <!--{{:Erőtan I. - Futószalag}}{{Megoldás|link=Erőtan I. - Futószalag}}--> | ||
A lap jelenlegi, 2014. november 10., 21:41-kori változata
Feladatok
- (2.1.2) Egy
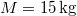 tömegű terhet álló helyzetből egyenletesen gyorsítva függőlegesen
tömegű terhet álló helyzetből egyenletesen gyorsítva függőlegesen 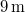 magasságra emelünk.
magasságra emelünk.
- a) Mekkora a gyorsulás, ha a végsebesség
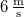 ?
?
- b) Mekkora erő szükséges a mozgatáshoz?
- c) Mennyi ideig tart a mozgás és mekkora az átlagsebesség az utolsó másodpercben?
- a) Mekkora a gyorsulás, ha a végsebesség
- (2.1.4) Egy autót
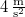 gyorsulással indítanak. A vezető az 5. másodperc végén akadályt pillant meg és
gyorsulással indítanak. A vezető az 5. másodperc végén akadályt pillant meg és 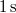 telik el a fékezés megkezdéséig. Hány métert halad az autó az akadály megpillantása után, ha a fék a kerekeket teljesen lefékezi? Mennyit haladt volna, ha a vezető azonnal fékez? A lefékezett autó és az úttest közötti súrlódási tényező
telik el a fékezés megkezdéséig. Hány métert halad az autó az akadály megpillantása után, ha a fék a kerekeket teljesen lefékezi? Mennyit haladt volna, ha a vezető azonnal fékez? A lefékezett autó és az úttest közötti súrlódási tényező 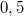 .
.
- (2.1.7) Egy vasúti kocsi rakománya és a kocsi padlója közötti súrlódási együttható
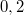 . A kocsi sebessége
. A kocsi sebessége 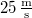 . Mekkora az a legrövidebb távolság, amelyen belül a kocsit a rakomány megcsúszásának veszélye nélkül állíthatjuk meg?
. Mekkora az a legrövidebb távolság, amelyen belül a kocsit a rakomány megcsúszásának veszélye nélkül állíthatjuk meg?
- (2.1.9) Vízszintes deszkán fekszik egy nagy tömegű test. A deszka és a teher közötti súrlódási együttható
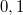 . Mekkora gyorsulást kell adnunk vízszintes irányban a deszkának, hogy a teher lemaradjon róla?
. Mekkora gyorsulást kell adnunk vízszintes irányban a deszkának, hogy a teher lemaradjon róla?
- (2.1.14) Egy
 hajlásszögű lejtő tetejéről a
hajlásszögű lejtő tetejéről a  időpontban elengedünk egy
időpontban elengedünk egy  tömegű testet, ugyanakkor el is kezdjük húzni a lejtővel párhuzamosan
tömegű testet, ugyanakkor el is kezdjük húzni a lejtővel párhuzamosan 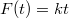 nagyságú erővel felfelé. A mozgást addig vizsgáljuk, míg a test újra meg nem áll. Numerikus adatok :
nagyságú erővel felfelé. A mozgást addig vizsgáljuk, míg a test újra meg nem áll. Numerikus adatok : 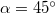 ,
, 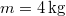 ,
, 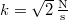 ,
, 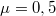 ,
, 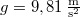 .
.
- a) Mekkora a test gyorsulása a
 időpontban?
időpontban?
- b) Add meg a test gyorsulását az idő függvényében! Mennyi idő telik el, míg a testre ható erők kiegyenlítik egymást?
- c) Mikor áll meg a test?
- d) Mekkora és milyen irányú a test gyorsulása a megállás pillanatában?
- e) Ha a lejtőt
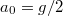 gyorsulással megtolnánk, mekkora lenne a test gyorsulása a
gyorsulással megtolnánk, mekkora lenne a test gyorsulása a  időpontban?
időpontban?
- a) Mekkora a test gyorsulása a
- (*2.1.16) Egy asztalon
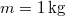 tömegű deszka, a deszkán
tömegű deszka, a deszkán 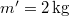 tömegű teher fekszik. Mekkora vízszintes irányú
tömegű teher fekszik. Mekkora vízszintes irányú  erővel kell hatni a deszkára, hogy az a teher alól kicsússzon? A teher és a deszka közötti tapadási-súrlódási együttható
erővel kell hatni a deszkára, hogy az a teher alól kicsússzon? A teher és a deszka közötti tapadási-súrlódási együttható 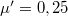 , a deszka és az asztal közötti tapadási-súrlódási együttható pedig
, a deszka és az asztal közötti tapadási-súrlódási együttható pedig 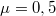 .
.
- (*2.1.26) Sima, vízszintes síkon levő kis méretű testre
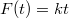 törvény szerint változó erő hat úgy, hogy iránya a vízszintessel
törvény szerint változó erő hat úgy, hogy iránya a vízszintessel  szöget zár be. A test és a sík közti súrlódástól eltekintünk. Határozza meg
szöget zár be. A test és a sík közti súrlódástól eltekintünk. Határozza meg
- a) a test sebességét abban a pillanatban, amikor a test kezd felemelkedni,
- b) a felemelkedés kezdetéig befutott utat! (
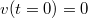 és
és 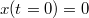 )
)
- (2.1.30) Megrakott
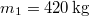 tömegű csille
tömegű csille 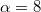 °-os lejtős pályán lefelé indul. Rakománya
°-os lejtős pályán lefelé indul. Rakománya 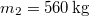 . A pályán a súrlódási tényező
. A pályán a súrlódási tényező 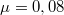 .
.
- a) Mekkora a gyorsulása?
- b) Mekkora a sebessége
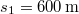 út befutása után?
út befutása után?
- c) Hány
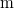 hosszú út befutása után kell megkezdeni a fékezést, ha azt akarjuk, hogy a kocsi
hosszú út befutása után kell megkezdeni a fékezést, ha azt akarjuk, hogy a kocsi 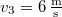 -nál jobban ne gyorsuljon fel?
-nál jobban ne gyorsuljon fel?
- d) Mekkora fékezőerőt kell alkalmazni a
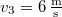 állandó sebesség fenntartására?
állandó sebesség fenntartására?
- e) Mennyi idő alatt fut le a kocsi a lejtőn, ha annak hossza
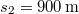 , és a
, és a 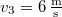 elérése után ezzel az állandó sebességgel halad tovább?
elérése után ezzel az állandó sebességgel halad tovább?
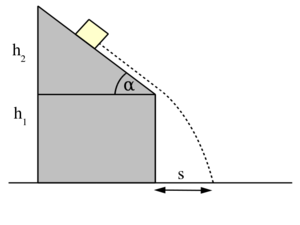
- (2.1.35) Vízszintes sík fölött
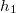 magasságban
magasságban  hajlásszögű,
hajlásszögű, 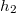 magasságú lejtőt helyezünk el. Ennek tetejéről test csúszik le, mely a vízszintesen mérve a lejtő csúcsától
magasságú lejtőt helyezünk el. Ennek tetejéről test csúszik le, mely a vízszintesen mérve a lejtő csúcsától  távolságban csapódik le. (2.1.35.ábra) Mennyi a lejtő és a test között a súrlódási együttható? (
távolságban csapódik le. (2.1.35.ábra) Mennyi a lejtő és a test között a súrlódási együttható? (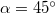 ,
, 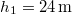 ,
, 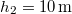 ,
, 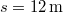 .)
.)
- (*2.1.38) Az
 hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel
hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel  szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható
szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható 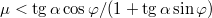 ?
?
- (*2.1.38) Egy
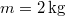 tömegű anyagi pontra
tömegű anyagi pontra 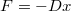 alakú rugalmas erő hat.
alakú rugalmas erő hat. 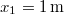 távolságban az erő nagysága
távolságban az erő nagysága 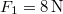 . A kezdő időpontban
. A kezdő időpontban 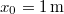 és
és 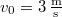 . Határozzuk meg a pont mozgását az idő függvényében!
. Határozzuk meg a pont mozgását az idő függvényében!
- (2.3.1) Tegyük fel, hogy egy műhold a földfelszín felett
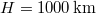 magasságban kering a Föld körül. Mekkora sebességgel kering, ha csak a Föld vonzóereje hat rá?
magasságban kering a Föld körül. Mekkora sebességgel kering, ha csak a Föld vonzóereje hat rá?
- (2.4.1) Egy
 tömegű golyóból és
tömegű golyóból és  hosszúságú, nyújthatatlan fonálból álló ingát a függőlegestől
hosszúságú, nyújthatatlan fonálból álló ingát a függőlegestől 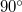 -kal kitérítünk, majd elengedünk. Mekkora erő feszíti a fonalat a golyó pályájának legalsó pontján való áthaladáskor? (A fonál tömege és a közegelenállás elhanyagolható.)
-kal kitérítünk, majd elengedünk. Mekkora erő feszíti a fonalat a golyó pályájának legalsó pontján való áthaladáskor? (A fonál tömege és a közegelenállás elhanyagolható.)
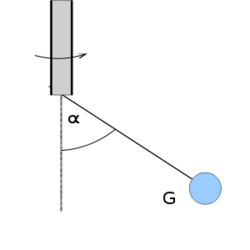
- (*2.4.4) Egy
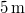 hosszú fonálon függő
hosszú fonálon függő 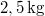 tömegű fémgömb egy motor tengelyére van szerelve. Mekkora a fonalat feszítő erő (
tömegű fémgömb egy motor tengelyére van szerelve. Mekkora a fonalat feszítő erő (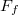 ) és mekkora szöggel hajlik ki az inga a függőlegestől, ha a motor fordulatszáma
) és mekkora szöggel hajlik ki az inga a függőlegestől, ha a motor fordulatszáma 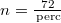 és feltesszük, hogy a fonál nem csavarodik meg a mozgás során?
és feltesszük, hogy a fonál nem csavarodik meg a mozgás során?
- (*2.4.7) Egy
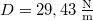 rugalmassági állandójú,
rugalmassági állandójú, 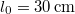 nyugalmi hosszúságú felfüggesztett rugó végére egy
nyugalmi hosszúságú felfüggesztett rugó végére egy 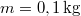 tömegű golyót helyezünk. A golyó állandó nagyságú sebességgel vízszintes kört ír le, miközben a rugó tengelye a függőlegessel
tömegű golyót helyezünk. A golyó állandó nagyságú sebességgel vízszintes kört ír le, miközben a rugó tengelye a függőlegessel 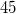 °-os szöget zár be. Mekkora a rugó megnyúlása és a golyó sebességének nagysága?
°-os szöget zár be. Mekkora a rugó megnyúlása és a golyó sebességének nagysága?
- Egy
 direkciós erejű rugó egyik végét a plafonhoz rögzítettük, másik végére pedig
direkciós erejű rugó egyik végét a plafonhoz rögzítettük, másik végére pedig  tömegű testet kötöttünk, amihez egy további fonalállal egy másik, szintén
tömegű testet kötöttünk, amihez egy további fonalállal egy másik, szintén  tömegű testet kötöttünk.
tömegű testet kötöttünk.
- a.) Mekkora a rugó megnyúlása egyensúlyi helyzetben?
- b.) Kicsit kitérítve az egyensúlyi helyzetből, mekkora lesz a kialakuló rezgés körfrekvenciája?
- Legyen ismét egyensúlyban a rendszer. Ekkor elvágjuk a fonalat.
- c.) Hol lesz az a rendszer új egyensúlyi helyzete?
- d.) Mekkora lesz az új körfrekvencia?
- e.) Mekkora amplitudójú rezgést végez a megmaradt test?
- f.) Adjuk meg a rezgés kitérés-idő függvényét!
-
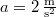
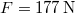
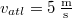
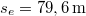
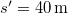
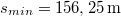
![\[a>1\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/5/1/1/5115683bbd049f166919a8ad5cc1e1d0.png)
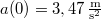
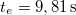
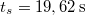
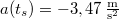
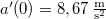
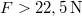
![\[v(t_{e})=\frac{mg^{2}\cos\alpha}{2k\sin^{2}\alpha}\]](/images/math/9/9/b/99be7a7462bdef1cafcb94c350ec5dd1.png)
![\[x(t_{e})=\frac{m^{2}g^{3}\cos\alpha}{6k^{2}\sin^{3}\alpha}\]](/images/math/d/d/3/dd3c3aaba1c23d6eb142f03e1b5c1980.png)
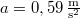
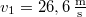
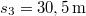
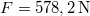
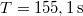
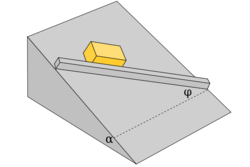
![\[a=g\left[\sin\alpha\sin\varphi-\mu\left(\cos\alpha+\sin\alpha\cos\varphi\right)\right]\]](/images/math/a/e/e/aee3124aefff6b6a7d9d979086ab9217.png)
![\[x(t)=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}\cos(\omega t-\varphi_{0})\]](/images/math/f/0/f/f0f93fed9161b63537f647c89aaa2454.png)