„Kinematika - 1.4.10” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 10. sor: | 10. sor: | ||
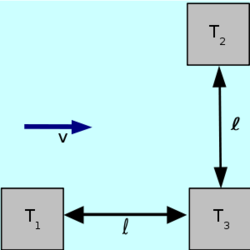
</noinclude><wlatex># Folyóvízben három tutaj van lehorgonyozva. $T_{1}T_{3}=T_{2}T_{3}=l$ , irányuk egymásra merőleges. A víz $T_{1}T_{3}$ irányában folyik $v$ sebességgel. Két gyorsúszó azonos, a vízhez képest $c>v$ sebességgel a $T_{3}$ tutajról egyszerre indulnak, az egyik a $T_{1}$ a másik a $T_{2}$ felé, ezeket megérintve visszatérnek $T_{3}$-hoz. Melyik ér vissza előbb, és mennyivel késik a másik?[[Kép:Kfgy_03_1_4_10.svg|none|250px]] | </noinclude><wlatex># Folyóvízben három tutaj van lehorgonyozva. $T_{1}T_{3}=T_{2}T_{3}=l$ , irányuk egymásra merőleges. A víz $T_{1}T_{3}$ irányában folyik $v$ sebességgel. Két gyorsúszó azonos, a vízhez képest $c>v$ sebességgel a $T_{3}$ tutajról egyszerre indulnak, az egyik a $T_{1}$ a másik a $T_{2}$ felé, ezeket megérintve visszatérnek $T_{3}$-hoz. Melyik ér vissza előbb, és mennyivel késik a másik?[[Kép:Kfgy_03_1_4_10.svg|none|250px]] | ||
</wlatex><includeonly><wlatex>{{Végeredmény|content=A $T_{2}$ tutajról induló úszó hamarabb ér vissza a saját tutajára}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=A $T_{2}$ tutajról induló úszó hamarabb ér vissza a saját tutajára}}</wlatex></includeonly><noinclude> | ||
| − | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: A $T_{1}$ tutajról induló úszót odafelé segíti a víz, visszafelé viszont hátráltatja. A visszaéréshez szükséges idő $$t_{13}=\frac{l}{c+v}+\frac{l}{c-v}$$ szerint számítható ki. A $T_{2}$ tutajról induló úszónak az odaúthoz szükséges idő $$t_{23,oda}=\frac{l}{\sqrt{c^{2}-v^{2}}}\,,$$ a visszafelé úthoz ugyanennyi időre van szüksége, így $$t_{23}=\frac{2l}{\sqrt{c^{2}-v^{2}}}\,.$$ A két időt összevetve azt találjuk, hogy $$t_{13} | + | <wlatex>#: A $T_{1}$ tutajról induló úszót odafelé segíti a víz, visszafelé viszont hátráltatja. A visszaéréshez szükséges idő $$t_{13}=\frac{l}{c+v}+\frac{l}{c-v}$$ szerint számítható ki. A $T_{2}$ tutajról induló úszónak az odaúthoz szükséges idő $$t_{23,oda}=\frac{l}{\sqrt{c^{2}-v^{2}}}\,,$$ a visszafelé úthoz ugyanennyi időre van szüksége, így $$t_{23}=\frac{2l}{\sqrt{c^{2}-v^{2}}}\,.$$ A két időt összevetve azt találjuk, hogy $$t_{13}>t_{23}\,,$$ vagyis a $T_{2}$ tutajról induló úszó hamarabb ér vissza a saját tutajára. Az idők közti különbség $$\Delta t=t_{13}-t_{23}=\frac{2l}{\sqrt{c^{2}-v^{2}}}\left[\frac{c}{\sqrt{c^{2}-v^{2}}}-1\right]\,.$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. augusztus 27., 12:57-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Folyóvízben három tutaj van lehorgonyozva.
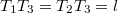, irányuk egymásra merőleges. A víz 
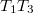irányában folyik 
sebességgel. Két gyorsúszó azonos, a vízhez képest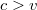 
sebességgel a 
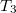tutajról egyszerre indulnak, az egyik a 
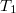a másik a 
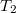felé, ezeket megérintve visszatérnek 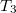-hoz. Melyik ér vissza előbb, és mennyivel késik a másik?
Megoldás
- A 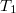tutajról induló úszót odafelé segíti a víz, visszafelé viszont hátráltatja. A visszaéréshez szükséges idő szerint számítható ki. A
![\[t_{13}=\frac{l}{c+v}+\frac{l}{c-v}\]](/images/math/b/7/2/b7236623471d5efd463581f549d5b383.png)
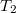tutajról induló úszónak az odaúthoz szükséges idő a visszafelé úthoz ugyanennyi időre van szüksége, így![\[t_{23,oda}=\frac{l}{\sqrt{c^{2}-v^{2}}}\,,\]](/images/math/a/0/6/a0676db3ac544a100ac9260af4ff560c.png)
A két időt összevetve azt találjuk, hogy![\[t_{23}=\frac{2l}{\sqrt{c^{2}-v^{2}}}\,.\]](/images/math/8/7/c/87ce2ef1e93d633a16d2a7d06468640a.png)
vagyis a![\[t_{13}>t_{23}\,,\]](/images/math/1/a/1/1a1c45c4861412ab69247a3133c4baf5.png)
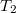tutajról induló úszó hamarabb ér vissza a saját tutajára. Az idők közti különbség ![\[\Delta t=t_{13}-t_{23}=\frac{2l}{\sqrt{c^{2}-v^{2}}}\left[\frac{c}{\sqrt{c^{2}-v^{2}}}-1\right]\,.\]](/images/math/9/7/0/970a6f503dd0ba7896d421fb22bb6d1f.png)
- A
