„Kinematika - 1.4.18” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 12. sor: | 12. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Tegyük fel, hogy a golyó a $t=0$ időpillanatban $r_{0}$ távolságban van az origótól és cső éppen vízszintes helyzetben, vagyis $\varphi_{0}$ és $\varphi(t)=\omega t$. A golyó mozgását először polár koordináták segítségével írjuk fel. $$r(t)=|r_{0}-v_{0}t|\qquad\qquad\varphi(t)=\omega t$$ Az abszolút értékkel figyelembe vettük azt az esetet is, amikor a golyó már áthaladt az origón. A polár koordináták alapján a Descartes-koordináták a külső megfigyelő rendszerében $$x(t)=r(t)\cos\varphi(t)=|r_{0}-v_{0}t|\cos(\omega t)$$$$ | + | <wlatex>#: Tegyük fel, hogy a golyó a $t=0$ időpillanatban $r_{0}$ távolságban van az origótól és cső éppen vízszintes helyzetben, vagyis $\varphi_{0}=0$ és $\varphi(t)=\omega t$. A golyó mozgását először polár koordináták segítségével írjuk fel. $$r(t)=|r_{0}-v_{0}t|\qquad\qquad\varphi(t)=\omega t$$ Az abszolút értékkel figyelembe vettük azt az esetet is, amikor a golyó már áthaladt az origón. A polár koordináták alapján a Descartes-koordináták a külső megfigyelő rendszerében $$x(t)=r(t)\cos\varphi(t)=|r_{0}-v_{0}t|\cos(\omega t)$$$$y(t)=r(t)\sin\varphi(t)=|r_{0}-v_{0}t|\sin(\omega t)\,.$$ |
| + | A sebesség, mint az idő függvénye, az alábbiak szerint írható fel. $$v_{x}(t)=\frac{dx}{dt}=$$ $$v_{y}(t)=\frac{dy}{dt}=$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. augusztus 27., 13:34-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy vékony egyenes cső
pontja körül állandó 
szögsebességgel forog vízszintes síkban. A csőben egy golyó mozog a csőhöz képest állandó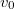 
sebességgel. Milyen pályát ír le a golyó a csövön kívül álló megfigyelőhöz képest és mekkora a sebessége, mint az idő függvénye?
Megoldás
- Tegyük fel, hogy a golyó a
időpillanatban 
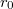távolságban van az origótól és cső éppen vízszintes helyzetben, vagyis 
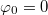és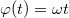 
. A golyó mozgását először polár koordináták segítségével írjuk fel. Az abszolút értékkel figyelembe vettük azt az esetet is, amikor a golyó már áthaladt az origón. A polár koordináták alapján a Descartes-koordináták a külső megfigyelő rendszerében![\[r(t)=|r_{0}-v_{0}t|\qquad\qquad\varphi(t)=\omega t\]](/images/math/2/f/3/2f311354494291e9ad9447a287e5a442.png)
![\[x(t)=r(t)\cos\varphi(t)=|r_{0}-v_{0}t|\cos(\omega t)\]](/images/math/1/b/5/1b54f1253d5a11bc70d46623d4bc8d3f.png)
![\[y(t)=r(t)\sin\varphi(t)=|r_{0}-v_{0}t|\sin(\omega t)\,.\]](/images/math/d/f/2/df2a5c451a8fa06e1eadf2abcd95de5f.png)
- Tegyük fel, hogy a golyó a
![\[v_{x}(t)=\frac{dx}{dt}=\]](/images/math/1/a/b/1ab501f4cb2bc788b335171d5def61a4.png)
![\[v_{y}(t)=\frac{dy}{dt}=\]](/images/math/8/e/d/8ed1103f21932bdeaff9d13ab1f85fd2.png)
