„Erőtan I. - 2.4.7” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Megoldás) |
||
| 12. sor: | 12. sor: | ||
== Megoldás == | == Megoldás == | ||
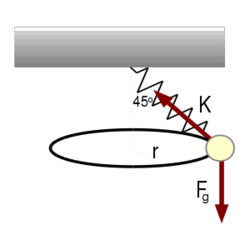
| − | <wlatex>#: A golyóra ható erőket az ábrán | + | <wlatex>#: A golyóra ható erőket az ábrán láthatjuk. |
| − | + | [[Kép:Kfgy_2_4_7M.svg|none|250px]] | |
Az eredő erő megegyezik a centripetális erővel, ezért $$K\cos\alpha=mg$$ $$K\sin\alpha=m\frac{v^{2}}{r}$$ A kötélerő $K=D\Delta l$, amelyből kifejezhető a megnyúlás és az első egyenlet alapján $$\Delta l=\frac{mg}{D\cos\alpha}=4,71\,\mathrm{cm}$$ A golyó által befutott kör sugara $r=(l_{0}+\Delta l)\sin\alpha$. Így a második egyenlet alapján $$v=\sqrt{(l_{0}+\Delta l)g\sin\alpha\,\mbox{tg}\,\alpha}=1,55\,\mathrm{\frac{m}{s}}\,.$$ | Az eredő erő megegyezik a centripetális erővel, ezért $$K\cos\alpha=mg$$ $$K\sin\alpha=m\frac{v^{2}}{r}$$ A kötélerő $K=D\Delta l$, amelyből kifejezhető a megnyúlás és az első egyenlet alapján $$\Delta l=\frac{mg}{D\cos\alpha}=4,71\,\mathrm{cm}$$ A golyó által befutott kör sugara $r=(l_{0}+\Delta l)\sin\alpha$. Így a második egyenlet alapján $$v=\sqrt{(l_{0}+\Delta l)g\sin\alpha\,\mbox{tg}\,\alpha}=1,55\,\mathrm{\frac{m}{s}}\,.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. június 24., 21:15-kori változata
Feladat
- Egy
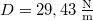rugalmassági állandójú, 
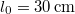nyugalmi hosszúságú felfüggesztett rugó végére egy 
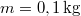tömegű golyót helyezünk. A golyó állandó nagyságú sebességgel vízszintes kört ír le, miközben a rugó tengelye a függőlegessel 
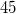°-os szöget zár be. Mekkora a rugó megnyúlása és a golyó sebességének nagysága?
Megoldás
- A golyóra ható erőket az ábrán láthatjuk.
![\[K\cos\alpha=mg\]](/images/math/6/9/e/69ebaef3efb9936c0e6cd9eee71f488e.png)
![\[K\sin\alpha=m\frac{v^{2}}{r}\]](/images/math/f/3/5/f355400db77912f663644276794d6503.png)
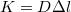, amelyből kifejezhető a megnyúlás és az első egyenlet alapján ![\[\Delta l=\frac{mg}{D\cos\alpha}=4,71\,\mathrm{cm}\]](/images/math/b/a/a/baae303c7f080e6d04c03aa5103158c2.png)
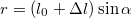. Így a második egyenlet alapján ![\[v=\sqrt{(l_{0}+\Delta l)g\sin\alpha\,\mbox{tg}\,\alpha}=1,55\,\mathrm{\frac{m}{s}}\,.\]](/images/math/0/1/5/015b9c358d6f792f1f081e04eadf4236.png)
