„Erőtan I. - 2.4.4” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Megoldás) |
||
| 12. sor: | 12. sor: | ||
== Megoldás == | == Megoldás == | ||
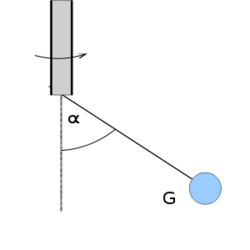
| − | <wlatex>#: Először számoljuk át a fordulatszámot körfrekvenciára. $$\omega=2,4\pi\frac{1}{\,\mathrm{s}}$$ A | + | <wlatex>#: Először számoljuk át a fordulatszámot körfrekvenciára. $$\omega=2,4\pi\frac{1}{\,\mathrm{s}}$$ A fémgömbbel együtt forgó vonatkoztatási rendszerben a rá ható erőket az ábrán ábrázoltuk. |
ÁBRA | ÁBRA | ||
Ebben a rendszerben a fémgömb nyugalomban van, ezért $$K\sin\alpha=F_{cf}\qquad\mbox{és}\qquad K\cos\alpha=F_{g}\,.$$ $$F_{cf}=m\omega^{2}l\sin\alpha\qquad\qquad F_{g}=mg$$ Ezek alapján $$K=m\omega^{2}l=72\pi^{2}\,\mathrm{N}$$ és $$\alpha=\arccos\left(\frac{g}{\omega^{2}l}\right)=88^{\circ}$$ | Ebben a rendszerben a fémgömb nyugalomban van, ezért $$K\sin\alpha=F_{cf}\qquad\mbox{és}\qquad K\cos\alpha=F_{g}\,.$$ $$F_{cf}=m\omega^{2}l\sin\alpha\qquad\qquad F_{g}=mg$$ Ezek alapján $$K=m\omega^{2}l=72\pi^{2}\,\mathrm{N}$$ és $$\alpha=\arccos\left(\frac{g}{\omega^{2}l}\right)=88^{\circ}$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. június 30., 15:20-kori változata
Feladat
- Egy
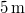hosszú fonálon függő 
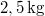tömegű fémgömb egy motor tengelyére van szerelve.(2.4.4. ábra) Mekkora a fonalat feszítő erő (
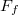) és mekkora szöggel hajlik ki az inga a függőlegestől, ha a motor fordulatszáma 
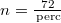és feltesszük, hogy a fonál nem csavarodik meg a mozgás során?
Megoldás
- Először számoljuk át a fordulatszámot körfrekvenciára. A fémgömbbel együtt forgó vonatkoztatási rendszerben a rá ható erőket az ábrán ábrázoltuk.
![\[\omega=2,4\pi\frac{1}{\,\mathrm{s}}\]](/images/math/a/8/9/a898dff84ef7dcb599129a3276e09044.png)
- Először számoljuk át a fordulatszámot körfrekvenciára.
ÁBRA
Ebben a rendszerben a fémgömb nyugalomban van, ezért![\[K\sin\alpha=F_{cf}\qquad\mbox{és}\qquad K\cos\alpha=F_{g}\,.\]](/images/math/7/5/e/75e6756207aaf8ab10276c62be54ed9f.png)
![\[F_{cf}=m\omega^{2}l\sin\alpha\qquad\qquad F_{g}=mg\]](/images/math/9/e/2/9e2911f2f4fa1126448574cf7a3d9f16.png)
![\[K=m\omega^{2}l=72\pi^{2}\,\mathrm{N}\]](/images/math/e/5/1/e51e8c42c66d7f453370cd00dec66dfd.png)
![\[\alpha=\arccos\left(\frac{g}{\omega^{2}l}\right)=88^{\circ}\]](/images/math/c/3/9/c39ecd0cfec5535093b844ca40c576cd.png)
